波利亚罐子模型及其应用

1 引言

第1章介绍基本的离散分布和一些现代工具，例如随机过程和可交换性。为了符合本书的目标和范围，我们会尽快切换到骨灰盒语言。分布的实现通过urn参数得以证实，所有概念的示例均以urns来表示。

第2章介绍了一些经典的概率问题。这些问题中的某些问题最初并不是作为problems问题给出的，但大多数问题都可以照原样重铸。

第三章

是关于作为离散基本结构并在离散时间内生长的双色P´olya骨灰盒的。

3.3  Bernard Friedman’s Urn

它的二维矩阵是这样子的，那么我们可以知道

 

 

3.4 The  Bagchi- Pal urn

 

 

 

 

第4章考虑了通过在Poisson过程中嵌入离散P´olya urn方案（称为泊松运算）而获得的连续时间的等效视图，从中可以得到P´olya过程。

第5章给出了启发性的论点，以将P'olya过程与离散的n方案（去沉松作用）联系起来。

第6章涉及几种扩展和概括（多色方案，随机加法）。

第7章提供了一个解析视图，可以获取和求解矩生成函数的函数方程。

第8章

是关于随机树的应用，随机树是计算机科学中作为数据结构或算法分析模型而出现的种类。

树是没有循环或循环的图。 它们在计算机科学和工程应用中作为模型比比皆是：某些形式用作数据结构，其他形式可用作分析算法的主干，其他形式则对某些结构（例如Internet或社交网络）的增长进行建模。 在许多情况下，通过以不确定的方式添加新顶点，它们以随机方式增长。 存在各种概率模型来反映增长或存储的数据的各个方面。

 

 

 

8.1  搜索树

8.1.1  二叉搜索树

 

首先介绍第一个种树，这种树形式如下

 

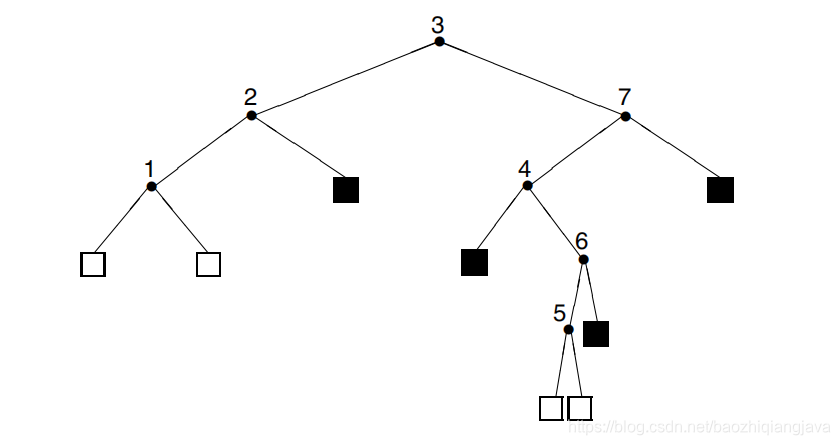
那么我们关心这种二叉树的生成和波利亚管子模型关系。这需要

1     将二叉树的构造过程和波利亚罐子模型等价构造

2  利用波利亚管子模型的结论来直接套用到该二叉树上，得到关于叶子节点/分支节点等等随机变量的分布。

首先介绍一个二维矩阵

 

 

从某种意义上说，在相应的2×2替换矩阵中，第一行代表撤回白球时所采取的动作，而第一列则包括当某球取回时所添加的白球数。

 

那么对于二叉树，其有如下二维矩阵和结论。

 

上面说明了二叉树的形成过程，以及其与波利亚管子模型的二维矩阵关系。那么就可以用有定理8.1 ，该定理8.1 的理论依据为定理3.5。如下

 

 

 

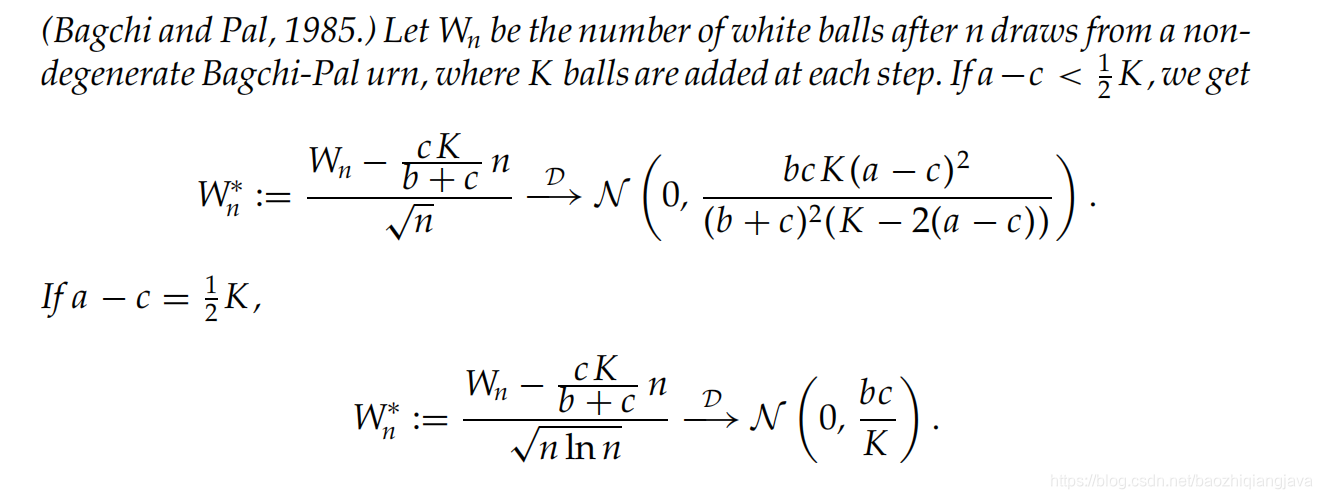
8.1.2   平衡树

 

这是另一种树，在这种树中。需要调整平衡，我们应该重点关注其对应的波利亚罐子模型过程。这比较抽象，这考验我们的等价代换思维。

暂时不考虑

 

8.1.3    m-ary 搜索树

 

8.1.4    2-3 Trees

 

 

8.1.6  铲斗四叉树

 

8.2   递归树

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

第9章讨论了生物科学中的应用（进化，系统发育，竞争排斥，传染和 临床试验），出现其他类型的P´olya骨灰盒。

第10章

适用于因多个球的绘制和应用而演变的骨灰盒。

就是一次性抽取多个球出来，比如2中颜色球，每次抽取两个。

10.1  抽成对的球出来的情况

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

所有章节的末尾都有练习。 练习的质量从容易到具有挑战性，相差很大，因此，我们在书的末尾添加了解决方案，有时在适当的时候添加一些额外的材料或说明可以在整个范围上提供更多的启发。