最优化理论公式大赏（上）

基本知识

基础

• 当矩阵的各阶顺序主子式$\left|\begin{array}{c}{a}_{11}\end{array}\right|,\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|,\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|,\cdots$皆>0时，矩阵正定；若奇数阶顺序主子式为负，偶数阶顺序主子式为正，则负定。
• 凸集：对凸集内的任意n点${\vec{x}}_i$，若有$\sum k_i=1$，则点$\sum k_i{\vec{x}}_i$也在该凸集中
• 凸函数：在非空凸集内，对其中任意两点${\vec{x}}_1,{\vec{x}}_2$和任意常数k∈(0,1)，都有$f(k{\vec{x}}_1+(1-k){\vec{x}}_2)\ge kf({\vec{x}}_1)+(1-k)f({\vec{x}}_2)$，则f为上凸函数，反之为下凸。
• 凸规划指在凸集上对由凸函数约束的凸目标函数做规划。若约束函数为凸线性函数，目标函数为凸二次函数，则该规划为凸二次规划。

多元泰勒展开

• 多元函数的梯度（以三元函数为例）：$\nabla f(\vec{x})={\left[\begin{array}{c}\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\end{array}\right]}^T$
• 多元函数的Hessian矩阵（以三元函数为例）：$H={\nabla }^{2}f(\vec{x})=\left[\begin{array}{ccc}\frac{{\partial }^{2}f}{\partial x_1\partial x_1}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_3}\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2\partial x_2}& \frac{{\partial }^{2}f}{\partial x_2\partial x_3}\\ \frac{{\partial }^{2}f}{\partial x_3\partial x_1}& \frac{{\partial }^{2}f}{\partial x_3\partial x_2}& \frac{{\partial }^{2}f}{\partial x_3\partial x_3}\end{array}\right]$
• 多元函数$f(\vec{x})$在${\vec{x}}_0$点的二阶泰勒展开式：
  $f(\vec{x})=f({\vec{x}}_0)+[\vec{x}-{\vec{x}}_0{]}^T\nabla f({\vec{x}}_0)+\frac{1}{2!}[\vec{x}-{\vec{x}}_0{]}^T{\nabla }^{2}f({\vec{x}}_0)[\vec{x}-{\vec{x}}_0]+o(||\vec{x}-{\vec{x}}_0|{|}^2)$
• 多元函数的稳定点：使$\nabla f({\vec{x}}_0)=\vec{0}$的点，也叫驻点，可能是极值点或鞍点
• 多元函数的极值点：由泰勒展式得：极值点必为稳定点，在稳定点处，当H正定时为极小值点，H负定时为极大值点。
• 多元函数的方向导数：
  $\frac{\partial f(\vec{x})}{\partial \vec{s}}$
  $=\underset{||\Delta \vec{s}||\to 0}{\lim }\frac{f(\vec{x}+\Delta \vec{s})-f(\vec{x})}{||\Delta \vec{s}||}$
  $=\frac{1}{||\Delta \vec{s}||}(\frac{\partial f(\vec{x})}{\partial x_1}\Delta x_1+\frac{\partial f(\vec{x})}{\partial x_2}\Delta x_2+\cdots +\frac{\partial f(\vec{x})}{\partial x_n}\Delta x_n)$
  $=\frac{\partial f(\vec{x})}{\partial x_1}\cos {\alpha }_1+\frac{\partial f(\vec{x})}{\partial x_2}\cos {\alpha }_2+\cdots +\frac{\partial f(\vec{x})}{\partial x_n}\cos {\alpha }_n$
  $=[\nabla f({\vec{x}}_0){]}^T\vec{s}/||\vec{s}||$
  又因为上式$=||\nabla f({\vec{x}}_0)||\cos [\nabla f({\vec{x}}_0),\vec{s}]$，所以当${\vec{x}}_0,\vec{d}$同向时函数的方向导数最大，即沿梯度方向上升得最快。反之，沿负梯度方向$-\nabla f({\vec{x}}_0)$函数下降得最快。

线性规划（不考）

二次规划

多元二次型可表示为$f(\vec{x})={\vec{x}}^{T}A\vec{x}+B^T\vec{x}+C$，其梯度为$A\vec{x}+B$。
若A正定，则该二次型正定，即$f(\vec{x})\ge 0$，仅当$\vec{x}=\vec{0}$时$f(\vec{x})=0$。
同理有负定、半正定、半负定和不定。

无约束优化

优化的直接法不需要求导，间接法要求导。

一维搜索的进退法

• 若确定函数的某个极小值点在某个闭区间上，则称该闭区间为函数的搜索区间。
• 进退法通过确定三个呈“大-小-大”分布的点，可以确定函数的搜索区间。
• 进退法的计算步骤：

1. 给定一元函数f、初始步长h、初始点x₁。
2. 令x₂=x₁+h。
3. 若f(x_i+1)≤f(x_i)，则h=2h，x_i+1=x_i+h，回到第2步，即“下降则进”。
4. 若f(x_i+1)>f(x_i)，则h=-h，x_i+1=x₁+h，回到第2步，即“上升则退”。
5. 若确定了三个使函数值呈“大-小-大”分布的点，则将两个大点作为搜索区间的端点返回。

一维搜索的0.618法

• 进退法能够确定搜索区间，但有些方法还要求函数在搜索区间上是单峰函数，即只有一个极小值点。若只有一个极大值点，则称为单谷函数。
• 0.618法的分形性使其可以节省一些内存，即像二分法一样每步一般只需多计算一个点。
• 0.618法的计算步骤：

1. 给定搜索区间[a,b]、在搜索区间上是单峰函数的一元函数f、精度ε。
2. 计算该区间0.381点c₁=0.618a
   +0.381b、0.618点c₂=0.381a+0.618b。
3. 按以下代码计算端点a、b：

while b-a >= eps:
	if f(c1)>f(c2):
		a = c1; c1 = c2; c2 = 0.381*a + 0.618*b;
	elif f(c1)<f(c2):
		b = c2; c2 = c1; c1 = 0.618*a + 0.381*b;
	else:
		a = c1; b = c2; c1 = 0.618*a + 0.381*b; c2 = a+b-c1;
return a,b

• 0.618法的精度ε和计算次数n的关系为$0.618^n(b-a)<\epsilon$。

一维搜索的最速下降法

先求$\nabla f(\vec{x})$，在每步迭代时求步长α_k，使$f({\vec{x}}_{k+1})=f({\vec{x}}_k-{\alpha }_k\nabla f({\vec{x}}_k))$最小。当$||\nabla f(\vec{x})||\le \epsilon$时停止迭代。

一维搜索的牛顿法

• 牛顿法的基本思想是在极小值点附近用二阶泰勒多项式近似目标函数，进而求出极小点的估计值。
• 用牛顿迭代法求方程φ(x)=0的根时，有迭代公式$x_{k+1}=x_k-\frac{\phi (x_k)}{{\phi }^{\prime }(x_k)}$。
• 同理，在极小值点附近，求极小值点等同于求方程φ’(x)=0的根。
• 所以，牛顿法求极小值点的迭代公式为$x_{k+1}=x_k-\frac{{\phi }^{\prime }(x_k)}{{\phi }^{\prime \prime }(x_k)}$。
• 当初始点充分接近极小值点时，该方法至少二阶收敛。
• 了解其它一位优化方法：切线法、二次插值法、格点法

多维搜索的牛顿法

• 取函数在迭代点处的二阶近似泰勒展开式，然后用和一维搜索牛顿法类似的公式迭代求$\nabla f({\vec{x}}_k)$的零点即可。
• 迭代公式为${\vec{x}}_{k+1}={\vec{x}}_k-[{\nabla }^{2}f({\vec{x}}_k){]}^{-1}\nabla f({\vec{x}}_k)={\vec{x}}_k-H^{-1}\nabla f({\vec{x}}_k)$。
• 上式中，${\vec{s}}_k={\vec{x}}_k-H^{-1}\nabla f({\vec{x}}_k)$也被称为牛顿方向。
• 同理，当初始点充分接近极小值点时，该方法具有二阶收敛速率。

多维搜索的共轭梯度法

• 若方向${\vec{s}}_1$、${\vec{s}}_2$和对称正定矩阵A满足${\vec{s}}_1^{T}A{\vec{s}}_2=0$，则称这两个方向关于A共轭。
• 共轭梯度法的基本思想是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。
• 给定函数f和初始点${\vec{x}}_0$时，其计算步骤为：

1. 第一次搜索时，令搜索方向${\vec{s}}_0=-\nabla f({\vec{x}}_0)$，求出使${\vec{x}}_1={\vec{x}}_0+a_0{\vec{s}}_0$最小的a₀和相应的${\vec{x}}_1$。
2. 第二次搜索时，令${\vec{\beta }}_0=\frac{||\nabla f({\vec{x}}_1)|{|}^2}{||\nabla f({\vec{x}}_0)|{|}^2}$，${\vec{s}}_1={\beta }_0{\vec{s}}_0-\nabla f({\vec{x}}_1)$，求出使${\vec{x}}_2={\vec{x}}_1+a_1{\vec{s}}_1$的函数值最小的a₁和相应的${\vec{x}}_2$，循环。

• 了解其它多维优化方法：最速下降法、坐标轮换法、共轭方向法、单纯形法（反射、扩张、压缩）
• 共轭方向法不用算梯度，注意不要混淆。

有约束优化

基础

• 可行域：由若干约束条件$g_i(x)\le 0$所围成的区域。若一个点不在可行域内，就不用往下讨论了。
• 起作用约束：若某点在约束条件的可行域内，且恰好使约束条件$g_i(x)\le 0$变为等号，则g_i为该点的起作用约束。若变为小于号，则为不起作用约束。
• K-T条件：又叫库恩-塔克条件、Kuhn-Tucker条件。在极小化规划问题中，若${\vec{x}}_k$在各约束的可行域内，且对于各线性无关的起作用约束$g_i(\vec{x})\le 0$（或$g_i(\vec{x})=0$），存在各分量皆为非负数的$\vec{\lambda }$，使$\nabla L=\nabla [\vec{f}(x_k)+\sum {\lambda }_i{g}_i({\vec{x}}_k)]=\vec{0},{\lambda }_i{g}_i({\vec{x}}_k)=0$，则${\vec{x}}_k$点满足K-T条件，或称其为K-T点。这样的点是在约束条件上的极值点。
• 若凸规划问题中的可行点是K-T点（局部最优解），则其为全局最优解。

有约束优化的直接法

• 随机实验法：随机取$\vec{x}$并计算$f(\vec{x})$，直到$f(\vec{x})$几乎不变
• 随机方向法：在某点的某一圆上求f值，Δf增则r增，Δf减则r减小
• 复合型法：将单纯形与可行域相复合
• 可行方向法：不停沿使f递减且在可行域内的方向行进
• 投影法：将点投影到可行域边界上
• 线性逼近法：将非线性的约束和目标函数通过一阶泰勒展开式近似线性化

有约束优化的间接法

• 也叫“消元法”，其思路是将约束塞入目标函数，从而消去约束。分为直接消元法、拉格朗日乘子法、惩罚函数法。
• 设下文中的优化问题为：$\begin{array}{c}\min f(\vec{x}),\vec{x}\in {\mathbb{R}}^n\\ s.t.\{\begin{array}{c}{g}_i(\vec{x})\le 0\\ h_i(\vec{x})=0\end{array}\end{array}$

拉格朗日松弛因子法

• 先向各约束引入拉格朗日乘子，再向各不等式约束g_i引入松弛因子w_i，然后将原优化问题变为$\min L=f(\vec{x})-\sum {\lambda }_i[g_i(\vec{x})+w_i^2]-\sum {\lambda }_j{h}_j(\vec{x})$
• 令$\frac{\partial L}{\partial x_i}=\frac{\partial L}{\partial {\lambda }_j}=\frac{\partial L}{\partial w_k}=0$，借助驻点求出f的最小值。
• 若无不等式约束，则该方法即为高数和考研中的拉格朗日乘数法。

惩罚函数法

• 惩罚函数法的思路是借助惩罚函数把有约束问题转化为无约束问题。
• 内点惩罚函数法迭代时点在可行域内，点靠近可行域边界时，惩罚函数的值→+∞，因此它将边界化为“障碍”。
• 令惩罚函数$F=f(\vec{x})-r_k[\sum \frac{1}{g_i(\vec{x})}+\sum \frac{1}{h_j(\vec{x})}]$或易于求导的$F=f(\vec{x})-r_k[\sum \ln |g_i(\vec{x})|+\sum \ln |h_j(\vec{x})|]$，k为迭代次数，r_k为第k次迭代时的系数，且r_k>0，$\underset{k\to +\infty }{\lim }{r}_k=0$。
• 之后，令$\frac{\partial F}{\partial x_i}=0,r_k\to 0$，即可解得x^*。
• 此外，还有一种“外点法”，但它迭代时点在可行域外。

变分法

• 泛函的定义：若任取函数x(t)及自变量t，J[x(t)]都有一个对应的J，则J[x(t)]是以x(t)为宗量的泛函。特别地，t为x(t)的宗量。常见的泛函形如$J={\int }_a^{b}x(t)\mathrm{d}t$或$J={\sum }_{i=a}^{b}x(t_i)$。
  但是，$J={\int }_a^{t}x(t)\mathrm{d}t$不是泛函，因为J’(t)=x(t)。

• 拉格朗日问题：（用欧拉方程）求使目标泛函/评价指标$J={\int }_a^{b}L[x,\dot{x},t]\mathrm{d}t$最小的函数x^*(t)

• 常用指标：最小时间控制$J=b-a={\int }_a^{b}1\mathrm{d}t$，最小燃料消耗控制$J={\int }_a^b|u(t)|\mathrm{d}t$，最小能量控制$J={\int }_a^b{u}^2(t)\mathrm{d}t$。u代表系统的输入量，在数学上可看做一个x

• 欧拉方程：$\frac{\partial L}{\partial x}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{x}}$，若x为向量，则将欧拉方程中的x换成x的任一分量，该方程都成立

无状态约束时的边界条件或横截条件

• x(a)和x(b)固定：x(a)=x_a，x(b)=x_b
• x(a)固定，x(b)不定：x(a)=x_a，$\frac{\partial L}{\partial \dot{x}}{|}_{t=b}=0$，反之则交换各公式中的a和b，下同
• x(a)和x(b)不定：$\frac{\partial L}{\partial \dot{x}}{|}_{t=a}=\frac{\partial L}{\partial \dot{x}}{|}_{t=b}=0$
• b不定，x(a)固定，x(b)不定：x(a)=x_a，$\frac{\partial L}{\partial \dot{x}}{|}_{t=b}=0,L{|}_{t=b}=0$
• b不定，x(a)固定，x(b)受约束：x(a)=x_a，x(b)=φ(b)，$\{[\dot{\phi }(t)-\dot{x}(t)]\frac{\partial L}{\partial \dot{x}}+L\}{|}_{t=b}=0$
• a不定，x(a)受约束，x(b)固定：x(b)=x_b，x(a)=φ(a)，$\{[\dot{\phi }(t)-\dot{x}(t)]\frac{\partial L}{\partial \dot{x}}+L\}{|}_{t=a}=0$
• 无论是何种情况，欧拉方程都成立，也可借助哈密顿函数求解

有状态约束时的解法

• 求使性能指标$J=\theta +{\int }_a^{b}L\mathrm{d}x$最小的一组泛函X（用大写代表向量$\vec{x}$），但可能有一组状态约束$\dot{X}=f$（如${\dot{x}}_1=x_2,{\dot{x}}_2=u$）或终端约束$\Phi (b)=\vec{0}$

• 哈密顿函数$H=L+{\vec{\lambda }}^{T}f$

• 将f、H、Φ塞入J，可得辅助函数$J_0=\theta +{\vec{\mu }}^T\Phi +{\int }_a^b[L+{\vec{\lambda }}^T(f-\dot{X})]\mathrm{d}x=\theta +{\vec{\mu }}^T\Phi +{\int }_a^b(H-{\vec{\lambda }}^T\dot{X})\mathrm{d}x$，原问题转化为求使J₀最小的泛函X

• 由欧拉方程可得$\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{\partial X}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{\partial \dot{X}}$，即$\frac{\partial H}{\partial X}=-{\vec{\lambda }}^{\prime }$

• 由欧拉方程可得$\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{\partial \vec{u}}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{\partial {\vec{u}}^{\prime }}$，即$\frac{\partial H}{\partial \vec{u}}=\vec{0}$

• 由$\frac{\partial J_0}{\partial X}=\vec{0},\frac{\partial J_0}{\partial t}=\vec{0}$可得通用的横截条件为$[\frac{\partial \theta }{\partial X}+(\frac{\partial \Phi }{\partial X}{)}^T\vec{\mu }-\vec{\lambda }{]}_{t=b}=\vec{0}$和$[\frac{\partial \theta }{\partial t}+{\vec{\mu }}^T\frac{\partial \Phi }{\partial t}+H{]}_{t=b}=0$

• 由$\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{\partial \vec{\lambda }}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial (H-{\vec{\lambda }}^T\dot{X})}{{\vec{\lambda }}^{\prime }}$和$\frac{\partial J_0}{\partial \vec{\mu }}$得出的则是约束本身

例题

已知状态约束$\dot{X}=f=\left[\begin{array}{c}{x}_2\\ u\end{array}\right]$（即$x_1^{\prime }=x_2,x_2^{\prime }=u$），边界条件$x_1(0)=0,x_2(0)=0$和终端约束$\Phi (t_f)=x_1+x_2-t{|}_{t=t_f}=0$。求使性能指标$J={\int }_0^{t_f}\frac{1}{2}{u}^2\mathrm{d}x$最小的X^*和u^*。
解：

• 首先，哈密顿函数$H=L+{\lambda }^{T}f=\frac{1}{2}{u}^2+{\lambda }_1{x}_2+{\lambda }_{2}u$
• 由欧拉方程得$\frac{\partial H}{\partial X}=-{\vec{\lambda }}^{\prime }$可得$\{\begin{array}{c}0=-{\lambda }_1^{\prime }\\ {\lambda }_1=-{\lambda }_2^{\prime }\end{array}$，故$\{\begin{array}{c}{\lambda }_1=C_1\\ {\lambda }_2=-C_{1}t+C_2\end{array}$
• 由欧拉方程得$\frac{\partial H}{\partial \vec{u}}=\vec{0}$可得$u+{\lambda }_2=0,u=-{\lambda }_2=C_{1}t-C_2$
• 结合边界条件和状态约束可得$x_1=\frac{1}{6}{C}_1{t}^3-\frac{1}{2}{C}_2{t}^2,x_2=\frac{1}{2}{C}_1{t}^2-C_{2}t$
• 由横截条件$[\frac{\partial \theta }{\partial X}+(\frac{\partial {\Phi }^T}{\partial X})\vec{\mu }-\vec{\lambda }{]}_{t=t_f}=0$可得$\{\begin{array}{c}\mu ={\lambda }_1(t_f)=C_1\\ \mu ={\lambda }_2(t_f)=C_1{t}_f+C_2\end{array}$，故$C_1=C_1{t}_f+C_2$，$C_2=C_1-C_1{t}_f$
• 由终端约束得$x_1(t_f)+x_2(t_f)=t_f$，即$\frac{1}{6}{C}_1{t}_f^3-\frac{1}{2}{C}_2{t}_f^2+\frac{1}{2}{C}_1{t}_f^2-C_2{t}_f=t_f$，与上式联立可化简为$\frac{2}{3}{C}_1{t}_f^2+C_1{t}_f-C_1=1$
• 由横截条件$[\frac{\partial \theta }{\partial t}+{\vec{\mu }}^T\frac{\partial \Phi }{\partial t}+H{]}_{t=t_f}=0$可得
  $$\begin{gathered} [\mu (x_1^{\prime }+x_2^{\prime }-1)+\frac{1}{2}{u}^2+{\lambda }_1{x}_2+{\lambda }_{2}u{]}_{t=t_f} \\ =C_1(\frac{1}{2}{C}_1{t}_f^2-C_2{t}_f+C_1{t}_f-C_2-1)+\frac{1}{2}(C_1{t}_f-C_2{)}^2+C_1(\frac{1}{2}{C}_1{t}_f^2-C_2{t}_f)-(C_1{t}_f-C_2{)}^2 \\ =C_1(\frac{1}{2}{C}_1{t}_f^2+C_1{t}_f^2+C_1{t}_f-C_1-1)+\frac{1}{2}(2C_1{t}_f-C_1{)}^2+C_1(\frac{1}{2}{C}_1{t}_f^2+C_1{t}_f^2-C_1{t}_f)-(2C_1{t}_f-C_1{)}^2 \\ =C_1^2{t}_f^2+2C_1^2{t}_f-\frac{3}{2}{C}_1^2-C_1=0 \end{gathered}$$，即$C_1{t}_f^2+2C_1{t}_f-\frac{3}{2}{C}_1=1$
• 将$C_1{t}_f^2+2C_1{t}_f-\frac{3}{2}{C}_1=1$与$\frac{2}{3}{C}_1{t}_f^2+C_1{t}_f-C_1=1$相减并约去C₁可得$\frac{1}{3}{t}_f^2+C_1{t}_f+\frac{1}{2}=0$，解得$t_f=\frac{\sqrt{15}-3}{2}$
• 因此：$$\begin{gathered} {C}_1=\frac{1}{\frac{2}{3}{t}_f^2+t_f-1}=-\frac{3+\sqrt{15}}{3} \\ {C}_2=C_1(1-t_f)=-\frac{\sqrt{15}}{3} \\ {u}^{\ast }(t)=C_{1}t-C_2=-\frac{3+\sqrt{15}}{3}t+\frac{\sqrt{15}}{3} \\ {x}_1^{\ast }(t)=\frac{1}{6}{C}_1{t}^3-\frac{1}{2}{C}_2{t}^2=-\frac{3+\sqrt{15}}{18}{t}^3+\frac{\sqrt{15}}{6}{t}^2 \\ {x}_2^{\ast }(t)=\frac{1}{2}{C}_1{t}^2-C_{2}t=-\frac{3+\sqrt{15}}{6}{t}^2+\frac{\sqrt{15}}{3}t \end{gathered}$$

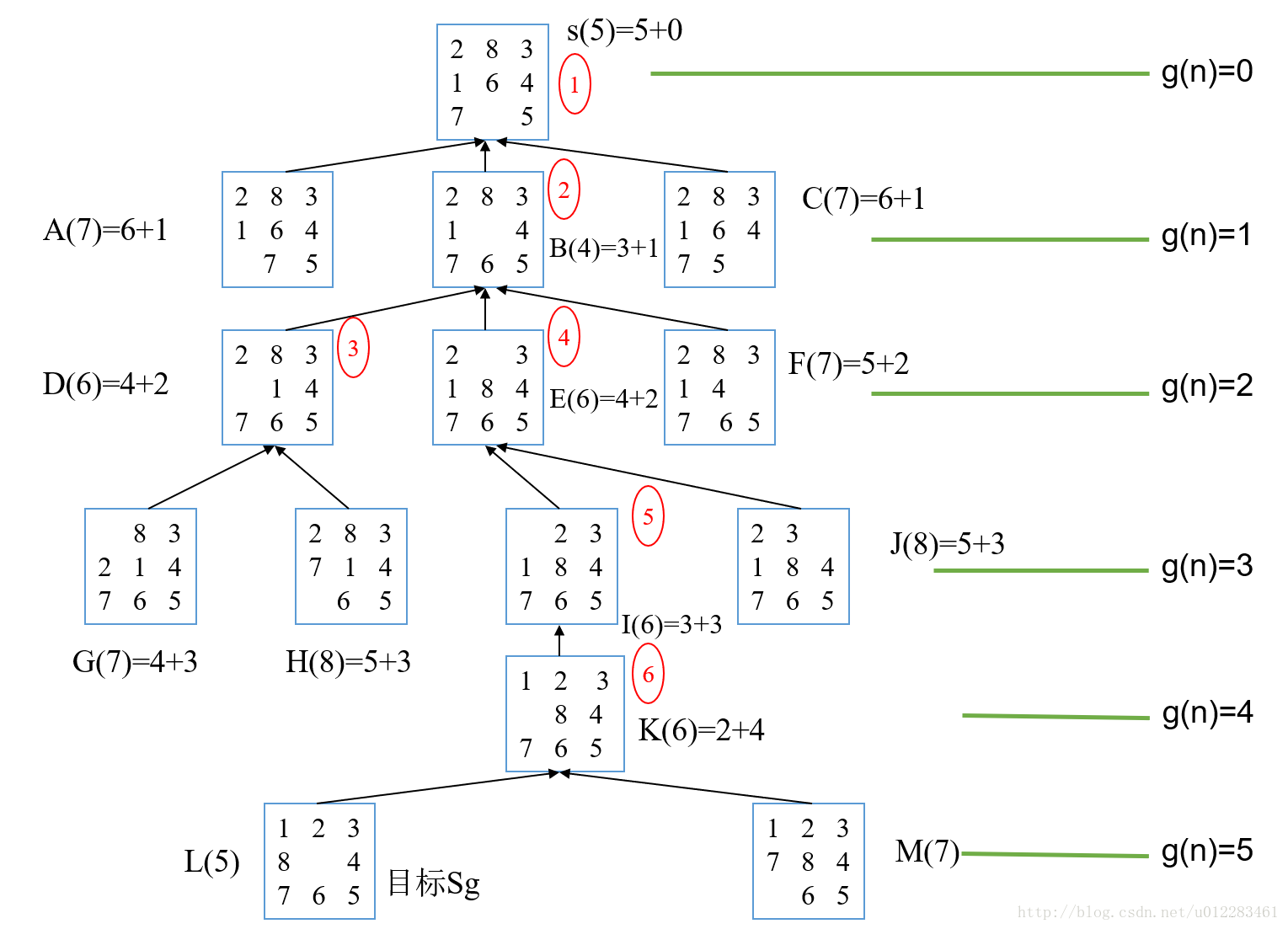
A*算法（图搜索算法）

• 图搜索算法分为深度/广度优先搜索等穷举法和A*算法、遗传算法等启发式算法
• 考试时可能要画出深度/广度优先搜索法的搜索顺序
• 在A*(n)算法中有f*(n)=g*(n)+h*(n)，即从起点到终点的最优路径=从起点到某点的最优路径+从该点到终点的最优路径。
• 在8数码问题（即三阶华容道）中，g*(n)为移动步数，h*(n)为misplaced(n)，即未归位数码的数量
• 该算法按f*(n)=g*(n)+h*(n)和h*(n)尽量小的方向搜索，直到用尽量少的步数解出该问题（如考试要考的8数码问题）
  

遗传算法

• 用遗传、变异和生存斗争法则来搜索全局最优解。
• 个体=一个向量，基因=向量的编码，环境适应性=目标函数，遗传操作=基因的继承/交换/变异，个体越适应环境越不易变异=目标函数越小，解越容易“存活”
• 考试时使用二进制编码，如向量[5,7,0]可编译为[“010101110000”]
• 给定自变量的取值范围[a,b]和精度ε，则每个维度的编码位数n满足$\frac{b-a}{2^n-1}\le \epsilon$，解码公式为$y_i=\frac{b-a}{2^n-1}{x}_i+a$
• 需设定的参数为遗传代数G（一般为100~500），种群数量M（一般为20~100），环境适应度（在优化问题中可以是目标函数的倒数，目标函数越小适应度越大），交叉互换概率p_c（一般为0.4~0.99）和变异概率p_m（一般为0.0001~0.1）。
• 在每次迭代中：
• • 首先淘汰一些适应度最小的个体，然后繁殖一些适应度最大的个体，使种群数量守恒。
• • 对每两个个体之间的相应基因片段，依概率p_c进行交叉互换。
• • 对每个个体的每一数位，依概率p_m进行变异。