实验技术与数据处理公式大赏

误差的基本性质与处理

• 误差可分为随机误差、系统误差、粗大误差三类。
• 首先计算算术平均值$\bar{x}=\frac{1}{n}\sum x_i$和残差$v_i=x_i-\bar{x}$。若在求平均数时选取了参考值x₀，则$\bar{x}=x_0+\frac{1}{n}\sum (x_i-x_0)$。
• 校核算术平均值和残差：设A为求得的$\bar{x}$的末位数的一个单位，当n为奇（偶）数时应有$|\sum v_i|\le \frac{n-1}{2}A$（$|\sum v_i|\le \frac{n}{2}A$），否则计算有误，应重新计算和校核
• 判断系统误差：设标准差$\sigma =\sqrt{\frac{\sum v_i^2}{n-1}}$，Peters标准差${\sigma }^{\prime }=\frac{5}{4}\cdot \frac{\sum |v_i|}{\sqrt{n(n-1)}}$，则算术平均值的标准差${\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{n}}$，平均误差$T\approx \frac{4}{5}{\sigma }_{\bar{x}}$，或然误差$R\approx \frac{2}{3}{\sigma }_{\bar{x}}$。若$|\frac{{\sigma }^{\prime }}{\sigma }-1|<\frac{2}{\sqrt{n-1}}$，则不存在系统误差，否则：
• • 若${\sum }_{1\sim m}{v}_i-{\sum }_{m\sim n}{v}_j$显然不为0，则存在线性系统误差。
• • 若$|v_1{v}_2+v_2{v}_3+\cdots +v_{n-1}{v}_n|>\sqrt{n-1}{\sigma }^2$，则存在周期性系统误差。
• 判断粗大误差：设显著性水平为α。n较大时采用3σ准则，n较小时采用格罗布斯准则：将x_i从小到大排列，若x₁（x_n）可疑，则令$g_1=\frac{\bar{x}-x_1}{\sigma }$（$g_n=\frac{{\bar{x}}_n-x}{\sigma }$）。查表得g₀(n,α)，若g_i≥g₀(n,α)，则应剔除x_i，然后重算$\bar{x}$和$\sigma$并循环此步。
• 求算术平均值的极限误差：n较多时，直接取${\delta }_{\lim }=3{\sigma }_{\bar{x}}$；n较少时，自由度为ν=n-1，查t分布表得t_α=t(n-1,α)，于是极限误差${\delta }_{\lim }(\bar{x})=t_{\alpha }{\sigma }_{\bar{x}}$。最终的测量结果为$L=\bar{x}\pm {\delta }_{\lim }(\bar{x})$。
• m次不等精度测量的加权合成：令权p₁:p₂:⋯=n₁:n₂:⋯，总的$\bar{x}=\frac{\sum p_i{\bar{x}}_i}{\sum p_i}$或$\bar{x}=x_0+\frac{\sum p_i({\bar{x}}_i-x_0)}{\sum p_i}，v_i={\bar{x}}_i-\bar{x},\sigma =\sqrt{\frac{\sum p_i{v}_i^2}{m-1}},{\sigma }_{{\bar{x}}_i}=\frac{\sigma }{\sqrt{n_i}},{\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{\sum p_i}}=\sqrt{\frac{\sum p_i{v}_i^2}{(m-1)\sum p_i}}$，最终的测量结果为$L=\bar{x}\pm 3{\sigma }_{\bar{x}}$。
• t检验法：假设有两组数据x~N(L₀,σ_x)和y~N(L₀,σ_y)。令$t=(\bar{x}-\bar{y})\sqrt{\frac{n_x{n}_y(n_x+n_y-2)}{(n_x+n_y)(n_x{\sigma }_x^2+n_y{\sigma }_y^2)}}$，当|t|<t(n_x+n_y-2,α)时无系统误差。

误差的合成与分配

• 由全微分公式得，基于多元函数$y=f(\vec{x})$的间接测量的系统误差为$\Delta y=\Delta f(\vec{x})=\sum \frac{\partial f}{\partial x_i}\Delta x_i$。
• 若有$\sin y=f$，因为$\Delta \sin y=\cos y\Delta y=\Delta f$，所以$\Delta y=\frac{\Delta f}{\cos y}$，其它函数同理。
• y的公称值为y₀，极限误差为${\delta }_{\lim }(y)=\sqrt{\sum [\frac{\partial f}{\partial x_i}{\delta }_{\lim }(x_i){]}^2}$，因此测量结果为$L=y_0-\Delta y\pm {\delta }_{\lim }(y)$。
• ${\delta }_{\lim }(x_i)$未知时，令${\sigma }_y=\sqrt{\sum (\frac{\partial f}{\partial x_i}{\sigma }_{x_i}{)}^2}$，则${\delta }_{\lim }(y)=3{\sigma }_y$。同理，若有$\sin y=f$，则${\sigma }_y=\frac{{\sigma }_f}{\cos y}$。
• 选择最佳测量方案：（1）令σ_y尽量小；（2）令误差传递系数$\frac{\partial f}{\partial x_i}=0$或尽量小
• 等作用分配原则：σ_y已知时，令$(\frac{\partial f}{\partial x_1}{\sigma }_{x_1}{)}^2=(\frac{\partial f}{\partial x_2}{\sigma }_{x_2}{)}^2=\cdots =(\frac{\partial f}{\partial x_n}{\sigma }_{x_n}{)}^2=\frac{{\sigma }_y^2}{n}$，从而求得${\sigma }_{x_i}=\frac{{\sigma }_y}{\sqrt{n}}/\frac{\partial f}{\partial x_i}$。δ_lim(y)已知时，同理可得${\delta }_{\lim }(x_i)=\frac{{\delta }_{\lim }(y)}{\sqrt{n}}/\frac{\partial f}{\partial x_i}$。

回归分析

• 拟合之前先画散点图。
• 求线性回归方程$\hat{y}=kx+b$的简易公式是$k=\frac{\sum x_i{y}_i-n\bar{x}\bar{y}}{\sum x_i^2-n{\bar{x}}^2},b=\bar{y}-k\bar{x}$。这是用最小二乘法求得的，即求$e=\sum (y_i-{\hat{y}}_i{)}^2$取最小值时的驻点。对于多元线性回归，只能用$X=(A^{T}A{)}^{-1}{A}^{T}B$。
• 曲线拟合过程可以通过换元变成线性回归。用直线法可检验模型的好坏，即将曲线换元成直线，然后描点画直线；用表差法也可检验模型的好坏，如要拟合y=ae^-x+b，，可以作列表Δy→lnΔy→ΔlnΔy，若ΔlnΔy近似为常数，则说明该模型可用。
• 评估线性回归的效果时，根据方差分析，有$U=\sum ({\hat{y}}_i-\bar{y}{)}^2,Q=\sum (y_i-{\hat{y}}_i{)}^2,\sigma =\sqrt{\frac{Q}{n-2}}$。
• 在显著性检验中，有${\nu }_U=1,{\nu }_Q=n-2,F=\frac{U}{{\nu }_U}/\frac{Q}{{\nu }_Q}$。此时若$F\ge F_{\alpha }(1,n-2)$，则称回归在α水平上显著，否则称x和y的线性关系不密切。
• 评估曲线拟合效果时，相关指数$R^2=1-\frac{Q}{\sum (y_i-\bar{y}{)}^2}$越接近1，拟合效果就越好。用换元前的因变量进行计算。

谐波分析

傅里叶级数

• 在[0,2π)上满足Dirichlet条件的函数的傅里叶级数为$\{\begin{array}{c}f(x)=A_0+\sum (A_n\cos nx+B_n\sin nx)\\ A_0=\frac{1}{2\pi }{\int }_0^{2\pi }f(x)\mathrm{d}x\\ A_n=\frac{1}{\pi }{\int }_0^{2\pi }f(x)\cos nx\mathrm{d}x\\ B_n=\frac{1}{\pi }{\int }_0^{2\pi }f(x)\sin nx\mathrm{d}x\end{array}$
• 在0~2π内取n等分点处的数据，然后用最小二乘原理（回归方程）可以硬解出傅里叶系数。
  令A_n=C_nsinφ，B_n=C_ncosφ，则A_ncos(nx)+B_nsin(nx)=C_nsin(nx+φ)称为第n阶谐波分量，$C_n=\sqrt{A_n^2+B_n^2}$为其振幅，$\phi =\arctan \frac{A_n}{B_n}$为其初相位。

傅里叶变换

• 圆频率f与角频率ω的关系是ω=2πf
• 随机过程的均值为$m_x(t)=E[x(t)]$，即x(t)的一阶原点矩。
• 随机过程的方差为$D_x(t)=E([x(t)-m_x(t){]}^2)$，即x(t)的二阶中心矩。标准差为${\sigma }_x(t)=\sqrt{D_x(t)}$。
• 随机过程的均方值为${\psi }_x^2(t)=E([x^2(t)])=m_x^2(t)+{\sigma }_x^2(t)$，即x(t)的二阶原点矩。
• 随机过程的自相关函数为$K_x(\tau )=E([x(t)-m_x(t)][x(t+\tau )-m_x(t+\tau )])$
• D_x=K_x(0)
• 随机过程的标准自相关函数为${\rho }_x(t,t+\tau )=\frac{K_x(t,t+\tau )}{{\sigma }_x(t){\sigma }_x(t+\tau )},{\rho }_x(\tau )=\frac{K_x(\tau )}{D_x}$。
• 信号x(t)与频谱x(f)互为傅里叶变换：
  $x(f)={\int }_{-\infty }^{+\infty }x(t)e^{-i\omega t}\mathrm{d}t,x(t)={\int }_{-\infty }^{+\infty }x(f)e^{-i\omega t}\mathrm{d}f$
  频率成分f的大小为|x(f)|，初相位为Arg[x(f)]。
• 双边谱密度函数S_x(ω)与K_x(τ)互为傅里叶变换：
  $$\begin{gathered} S_x(\omega )=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{K}_x(\tau )e^{-i\omega \tau }\mathrm{d}\tau =\frac{1}{\pi }{\int }_0^{+\infty }{K}_x(\tau )\cos (\omega \tau )\mathrm{d}\tau \\ {K}_x(\tau )={\int }_{-\infty }^{+\infty }{S}_x(\omega )e^{i\omega \tau }\mathrm{d}\omega =2{\int }_0^{+\infty }{S}_x(\omega )\cos (\omega \tau )\mathrm{d}\omega \end{gathered}$$
• K_x(τ)为常函数或正/余弦函数的组合时，S_x(ω)为冲激函数的组合。令τ=0，上式两端变为$K_x(0)={\int }_{-\infty }^{+\infty }{S}_x(\omega )\mathrm{d}\omega$，由此可以确定冲激函数的系数。
• 单边谱密度G_x(f)=2S_x(f)，且它的f≥0。
• 采样定理：信号不失真时，采样频率f_s和信号的最高频率分量f_m满足f_s≥2f_m。

动态测试数据处理的基本方法

动态测试数据的分类：

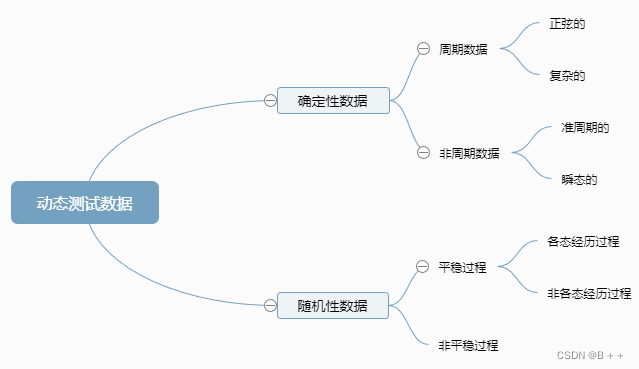
• 平稳过程的均值和方差为常数。
• 若每次实验时，上述常数都（不一定）相同，则该平稳过程为（非）各态历经过程。