一、简单相加
符号∑(sigma)通常用于表示多个项的总和。这个符号通常伴随着一个索引,该索引变化以包含总和中必须考虑的所有术语。
例如,݊第一个整数的和可以用以下方式表示:
或者 ,这两种表示意思都是一样的。
,这两种表示意思都是一样的。
更一般地说,表达式表示n项的总和
1、示例1
给定,
,
,
,
。
分别计算和
。


2、简单规则
下图中c代表常数。
规则一中的常数可以提取出来。
规则二中的求和等于n个c相乘。
规则三中的相加等于分别求和。

3、示例2
给定,
,
,
,
。并且
,
,
,
,
。
分别计算,
,
。
从上面公式可知
(1)


(2)

(3)
4、需要注意
 和
和 不是一回事。
不是一回事。
 和
和 不是一回事。
不是一回事。
5、示例3
给定,
,
,
,
。并且
,
,
,
,
。


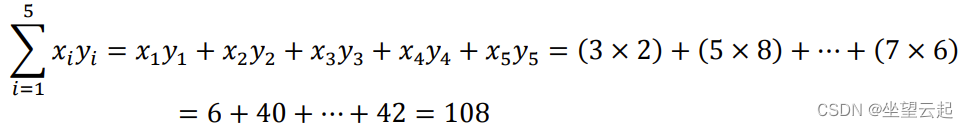
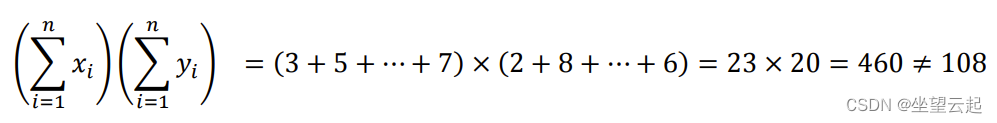
二、双索引的情况
1、示例1
给定,
,
。并且
,
。
我们将对x的项使用索引i,对y的项使用索引j。
于是我们的到如下
为了表示表格或矩阵的数据,我们经常见到或使用双索引表示法,如其中第一索引(i)对应于数据所在的行的编号,第二索引(j)对应于列。例如,术语
表示位于表或矩阵的第2行和第4列的交叉点处的数据。
2、示例2
给定如下矩阵定义

要求一行的项的和,我们必须固定该行的索引,并对所有可能的值更改列的索引。例如:
下图分别计算了第一行和第二行的和。

要求一列的项的和,必须固定该列的索引,并对所有可能的值更改行的索引。
下图计算了第四列的和

要对表中的所有项求和,必须更改两个索引并使用双和:
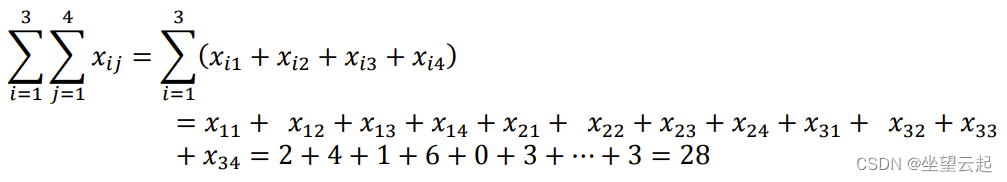








 文章介绍了数学中Σ符号用于表示项的总和,通过示例解释了单索引和双索引求和的概念,包括如何处理常数项,以及如何在矩阵和表格数据中应用双索引。同时强调了不同求和的区别,并提供了计算特定行和列和的方法。
文章介绍了数学中Σ符号用于表示项的总和,通过示例解释了单索引和双索引求和的概念,包括如何处理常数项,以及如何在矩阵和表格数据中应用双索引。同时强调了不同求和的区别,并提供了计算特定行和列和的方法。



















 399
399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










