1. 统计语言模型 (statistical model of language)
统计语言模型中,把一段包含T个词的语料表示为
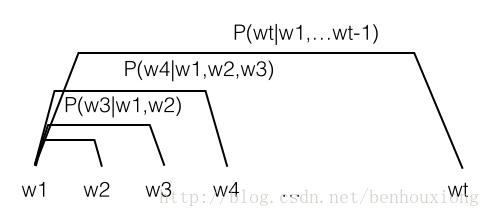
w_t 表示第t个词,统计每个词在前面n个词出现的条件下的概率,用一幅图来表达就是:
应用这个模型的时候,为了降低复杂度,基于马尔科夫假设(Markov Assumption):下一个词的出现仅依赖于它前面的一个或几个词,上面的公式可以近似为:
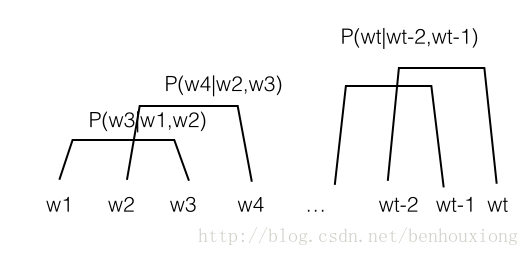
上面那张图就变成(n=2):
这就变成了n-gram 模型,也就是构造了一个每个词关于最近n个词的条件概率表。
那么,我们在面临实际问题时,如何选择依赖词的个数,即n。
- 更大的n:对下一个词出现的约束信息更多,具有更大的辨别力;
- 更小的n:在训练语料库中出现的次数更多,具有更可靠的统计信息,具有更高的可靠性。
- 由于训练语料限制,无法追求更大的n
- 没有考虑到相似的语法结构。
- 将词典中每个词表示为向量
- 用词向量表示每个词在句子中的联合概率函数
- 同时学习词向量和联合概率函数参数
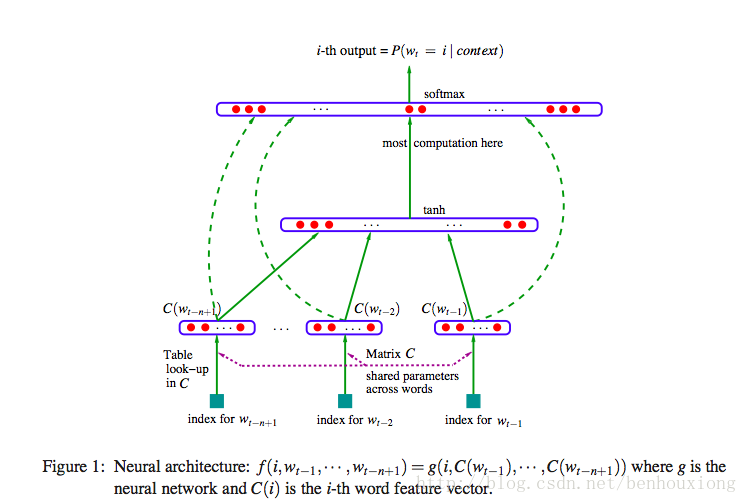
表示为一个神经网络:
最后一层是一个softmax
softmax输入表示为
其中x为
C(w_t) 表示将词 w_t向量化。
相当于有两层隐含层,一层向量化层C,一层tanh H。
需要学习的参数总共:θ = (b,d,W,U,H,C).
#θ = |V |(1 + nm + h) + h(1 + (n − 1)m).
V为词数,n为窗口大小,m为词向量维度,h为隐含层H的节点数。
使用最大似然最优化:
具体求解方法还请阅读paper
虽然模型在有限训练数据下,可以提高n的取值,且可以描述出更细致的词与词的关系,但模型优化计算复杂度要远高于n-gram,因为n-gram要得到一个样本的联合概率不需要计算词典中所有词的概率,而神经网络表达需要在最后一层softmax计算所有词的输出做归一化。
训练一个样本需要的计算复杂度是
|V |(1 + nm + h) + h(1 + nm) + nm
如果V很大的话,这个计算是非常耗时的,下篇我会介绍层次神经网络语言模型,通过把词表表示成一个树的结构,可以吧 |V| 降到 log|V|,使得问题可解。
参考文献
【A Neural Probabilistic Language Model 】








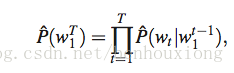
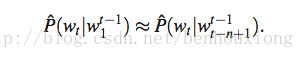
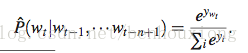

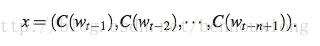
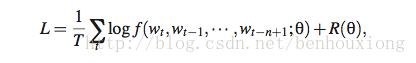














 1937
1937

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








