2D-2D：对极约束

对极约束

对极几何的地位：对极几何（Epipolar Geometry）是Structure from Motion问题中，相机在不同位置拍摄场景，所成两幅图像中对应坐标点存在的几何关系，是SFM中2D-2D求解两帧图像间相机位姿的基本模型。
匹配的特征点$p_1$，$p_2$。

两幅图像$I_1$，$I_2$。第一帧到第二帧图像的运动R，t。两个相机的中心分别为$O_1$，$O_2$。$I_1$中特征点$p_1$，在$I_2$上对应的特征点$p_2$。如果二者匹配正确，则两点对应同一空间点在两个成像平面上的投影。$p_1$，在$I_2$，$\overrightarrow{O_1{p}_1}$与$\overrightarrow{O_2{p}_2}$在三维空间中相交于点P。$O_1,O_2,P$三点可以确定一个平面，称为极平面（Epipolar plane）。$O_1{O}_2$称为基线（Baseline）。称极平面与两个像平面$I_1$，$I_2$的交线$l_1$，$l_2$，称为极线。

几何关系，从代数的角度描述

在第一帧的坐标系下，P的空间位置 ${\left[\begin{array}{ccc}X& Y& Z\end{array}\right]}^T$，根据针孔相机模型，相机成像平面一点的像素坐标$p$和该点在世界坐标系下的3D坐标$P$存在$p=KP$的关系，其中$K$为相机内参。采用齐次坐标表示为：$$dp=KP$$其中d是空间点深度（为了将$p$的齐次项变为1），$p$和$P$都是齐次坐标。以第一个相机坐标系作为参照，两个像素点的像素位置（up to scale）为$$d_1{p}_1=KP\text{\hspace{1em}(1)}$$$$d_2{p}_2=K(RP+t)\text{\hspace{1em}(2)}$$其中K为相机内参矩阵，R为从第一个相机坐标系到第二个相机坐标系的旋转矩阵（Rotation），t为从第一个相机坐标系到第二个相机坐标系的平移向量（Translation）。如果写成齐次坐标的形式，上式可写成非零常数下成立的等式：
$$p_1=KP\text{\hspace{1em}(3)}$$$$p_2=K(RP+t)\text{\hspace{1em}(4)}$$现在取：$$x_1=K^{-1}{p}_1\text{\hspace{1em}(5)}$$$$x_2=K^{-1}{p}_2\text{\hspace{1em}(6)}$$点$x_1，x_2$是两个像素点的归一化平面（相机坐标系？）上的坐标，带入上式得：$$x_2=R{x}_1+t\text{\hspace{1em}(7)}$$两边同时左乘$t^{\wedge }$，相当于两侧同时与t做外积:$$t^{\wedge }{x}_2=t^{\wedge }R{x}_1\text{\hspace{1em}(8)}$$两边同时左乘$x_2^T$:$$x_2^T{t}^{\wedge }{x}_2=x_2^T{t}^{\wedge }R{x}_1\text{\hspace{1em}(9)}$$观察等式左侧，$t^{\wedge }{x}_2$是一个与t和$x_2$都垂直的向量。把它再和$x_2$做内积时，将得到0。因此$$x_2^T{t}^{\wedge }R{x}_1=0\text{\hspace{1em}(10)}$$，重新带入$p_1,p_2$，有：$$p_2^T{K}^{-T}{t}^{\wedge }R{K}^{-1}{p}_1=0\text{\hspace{1em}(11)}$$(10),(11)式都称为对极约束。
将中间部分记作两个矩阵：
$$E=t^{\wedge }R,F=K^{-T}E{K}^{-1},x_2^{T}E{x}_1=p_2^{T}F{p}_1$$
对极约束描述了匹配点$x_2$在$E{x}_1$这条直线上这样的几何关系。相机位姿求解：

1. 通过匹配点对求解E或F。
2. 分解E或F求出R，t。
3. 备注：E和F只相差相机内参，SLAM通常已知内参，实践中采用形式更简洁的E。

几何关系，从几何的角度描述

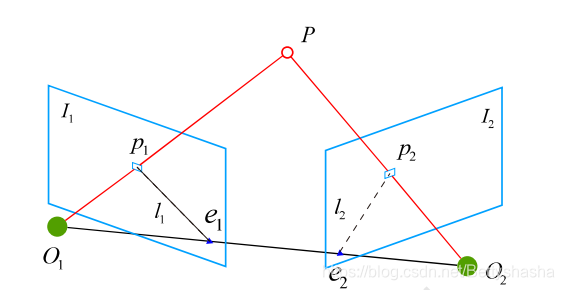
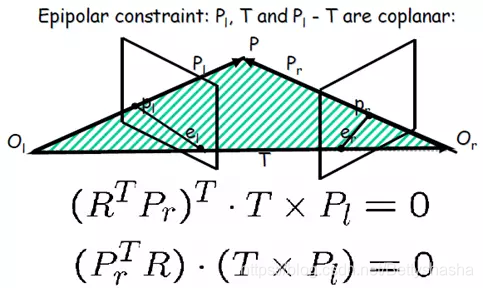
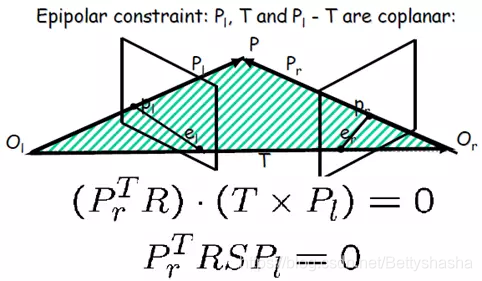
对极约束，几何解释1

如图，对极平面$O_1{O}_{2}P$，物点P在左像平面上的像点$p_l$,在左像平面上的像点$p_r$,左相机光心$O_1$在右像平面成像点$e_r$,右相机光心$O_2$在左像平面成像点$e_l$，其中$e_l，e_r$称为极点，$p_l{e}_l，p_r{e}_r$称为极线。对极约束描述的是物点在左相机平面上所成像点$p_l$，在右相机平面一定在极线$p_r{e}_r$上。

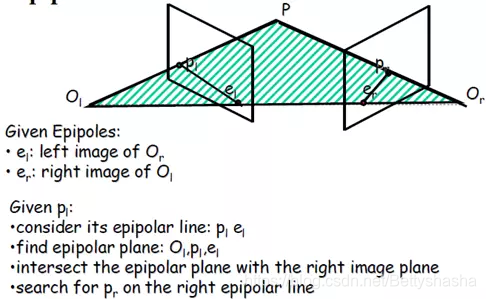
两个相机的坐标系存在如下关系：$x_2$

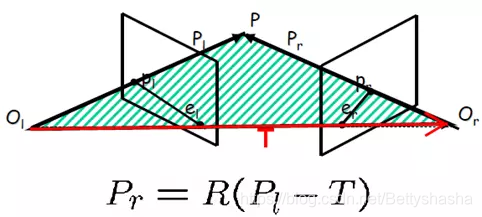
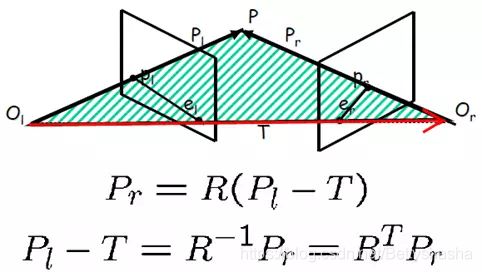
对极约束几何解释2

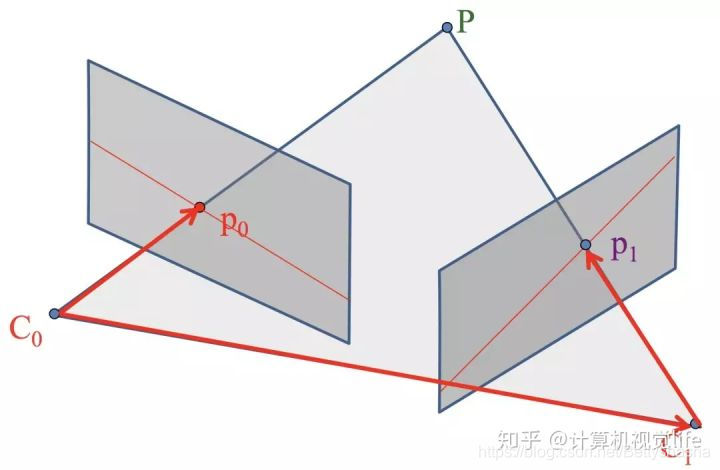
对极约束中很常见的图。它表示的是一个运动的相机在两个不同位置的成像，左右两个平行四边形分别是相机在不同位置的成像平面，$C_0,C_1$分别是两个位置中相机的光心，也就是针孔相机模型中的针孔$P$是空间中的一个三维点，$p_0{p}_1$分别是P点在不同成像平面上对应的像素点。$C_0{C}_{1}P{p}_0{p}_1$组成的平面叫极平面。

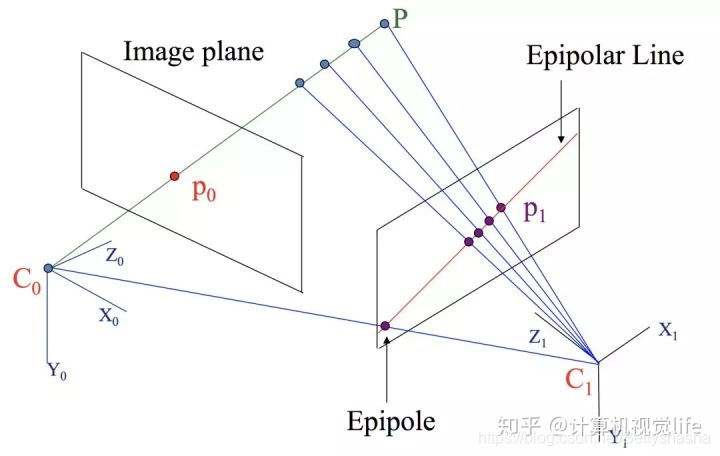
极平面与成像平面的交线叫极线，两个光心和成像平面的交点叫极点。


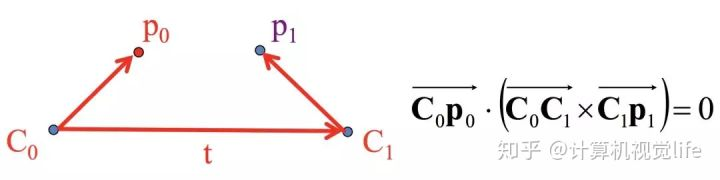
三个向量共面，即$$\overrightarrow{C_0{P}_0}\cdot (\overrightarrow{C_0{P}_0}\times \overrightarrow{C_1{P}_1}\text{\hspace{1em}(2-1)}$$
$p_0,p_1$都是图像上的二维点。把它们变成三维的方向向量来考虑，即只考虑方向，不考虑起点或终点。假设一个归一化的图像平面，该平面上焦距f=1,因此，在以$C_0$为原点的坐标系下，$p_0={\left(\begin{array}{ccc}{x}_0& y_0& 1\end{array}\right)}_{C_0}$,以$C_1$为坐标系$p_1={\left(\begin{array}{ccc}{x}_1& y_1& 1\end{array}\right)}_{C_1}$,在$C_0{C}_1{p}_0{p}_1$组成的极平面上，保证$\overrightarrow{C_0{P}_0}$的方向不变，在极平面上移动时，结论仍然成立。
$p_0，p_1$不在同一个坐标系里，将所有点的坐标都转换到以$p_0$为原点的坐标系，方向向量仅与方向有关，而与起始位置无关，因此只考虑旋转。从$C_1$坐标系到$C_0$坐标系的旋转矩阵R，那么$R{p}_1$就是$p_1$在以$C_0$为原点的坐标系中的坐标了。
对$$\overrightarrow{C_0{P}_0}\cdot (\overrightarrow{C_0{P}_0}\times \overrightarrow{C_1{P}_1}\text{\hspace{1em}(2-1)}$$最左边向量$C_0{p}_0$可以用$p_0$表示，向量$C_0{C}_1$就是光心$C_1$相对于$C_0$的平移，记为t，向量$C_1{p}_1$根据前面的结论，可以用$R{p}_1$表示，因此上式可表达为：
$$p_0\cdot (t\times R{p}_1)$$
这个式子是根据对极几何得到的，因此称为对极约束。
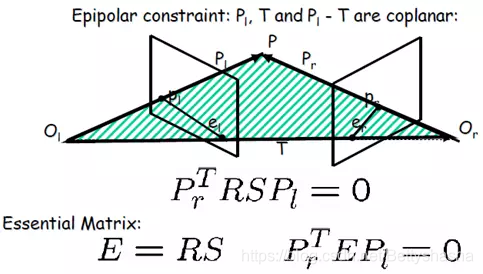
其中$$(t\times R)=t^{\wedge }R=E$$称为本质矩阵或本征矩阵。因此：$$p_{0}E{p}_1=0$$根据此式，可求出极线方程。
根据理论：点$p$在直线$l$上的充分必要条件是直线$l$的系数与$p$的齐次坐标$p^{\prime }$的内积为0。即$$l^T\cdot p^{\prime }=0$$
将$E{p}_1$看作是直线的方程，$p_0$看作是直线上的点，即$E{p}_1$是以$C_0$为原点坐标系中的极线了。如图中红线所示：

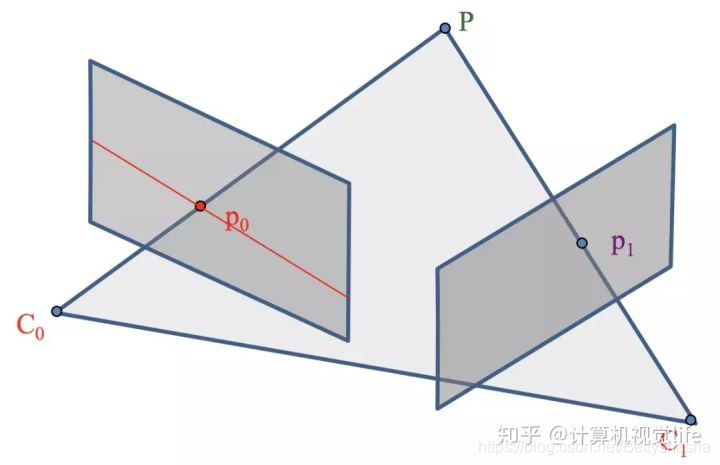
题目：现有一个运动着的相机拍摄的连续两张图片，其中特征点匹配部分已经完成。请根据两帧图像对应的匹配点计算基础矩阵，并利用该矩阵绘制出前10个特征点对应的极线。

注释

叉乘与矩阵和向量相乘的变换推导

向量$a=\left[\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right]$,$b=\left[\begin{array}{ccc}{b}_1& b_2& b_3\end{array}\right]$,内积描述向量间的投影关系，$$a\cdot b=a^{T}b=\sum _{i=1}^3{a}_i{b}_i=|a||b|cos⟨a,b⟩$$
外积描述两个向量张成的四边形的有向面积：$$a\times b=\left[\begin{array}{ccc}i& j& k\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right]=\left[\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right]b\stackrel{△}{=}\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]b=a^{\wedge }b$$。引入${}^{\wedge }$符号（反对称符号），把a写成一个反对称矩阵，可以把$a\times b$写成矩阵与向量的乘法$a^{\wedge }b$，把外积变成了线性运算。外积只对三维向量存在定义。外积还可以表示向量的旋转。a到b的旋转可以通过右手定则来确定方向，用a,b之间的夹角确定大小，用3个实数来描述，即向量$\omega$。

叉乘与点乘的关系

两个向量的叉乘结果是一个同时垂直于这两个向量的向量。
叉乘只在三维空间中有定义，比如两个向量 a和b 的叉乘写作 a x b，它是与向量 a, b都垂直的向量，其方向通过右手定则决定。
除了叉乘，还有点乘，a点乘b的定义是
$$a\cdot b=|a||b|cos(\theta )$$

因此如果两个互相垂直的向量点乘，cos(θ) = 0，点乘结果也为0。

点p在直线上的充分必要条件是直线l的系数与p的齐次坐标$p^{\prime }$的内积为0

$$l^T{\dot{p}}^{\prime }=0$$

初次整理笔记，理解还不是特别深刻，先到这吧，以后有了新理解再来补充。

参考文献

《视觉SLAM十四讲：从理论到实践》第7讲7.3.1
从零开始一起学习SLAM | 不推公式，如何真正理解对极约束? https://zhuanlan.zhihu.com/p/48666442
https://www.cnblogs.com/clarenceliang/p/6704970.html
https://www.jianshu.com/p/032e61a23cc0