例题一:字符串哈希link


思路:
字符串hash模板题,
按照上述的字符串hash求出字符创的hash值,
然后进行排序即可求出答案。
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<queue>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#define ll long long
using namespace std;
const int MAX = 2147483647;
const int N = 1e9 + 7;
const int Mod = 13331;
int n, ans;
string s, hash[Mod + 100];
bool h()
{
int len = s.size();
ll num = 0;
for(int i = 0; i <= len; i++) num = num * 64 + int(s[i]), num %= N;
num %= Mod;
if(hash[num] == s) return 1;
if(hash[num] != s && hash[num] != "")
{
int i = num + 1;
i %= Mod;
while(i != num)
{
if(hash[i] == s) return 1;
if(hash[i] == "") {hash[i] = s; return 0;}
i = (i + 1) % Mod;
}
}
hash[num] = s;
return 0;
}
int main()
{
//fre();
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
cin >> s;
if(!h()) ans++;
}
printf("%d", ans);
return 0;
}
例题二:回文子串link
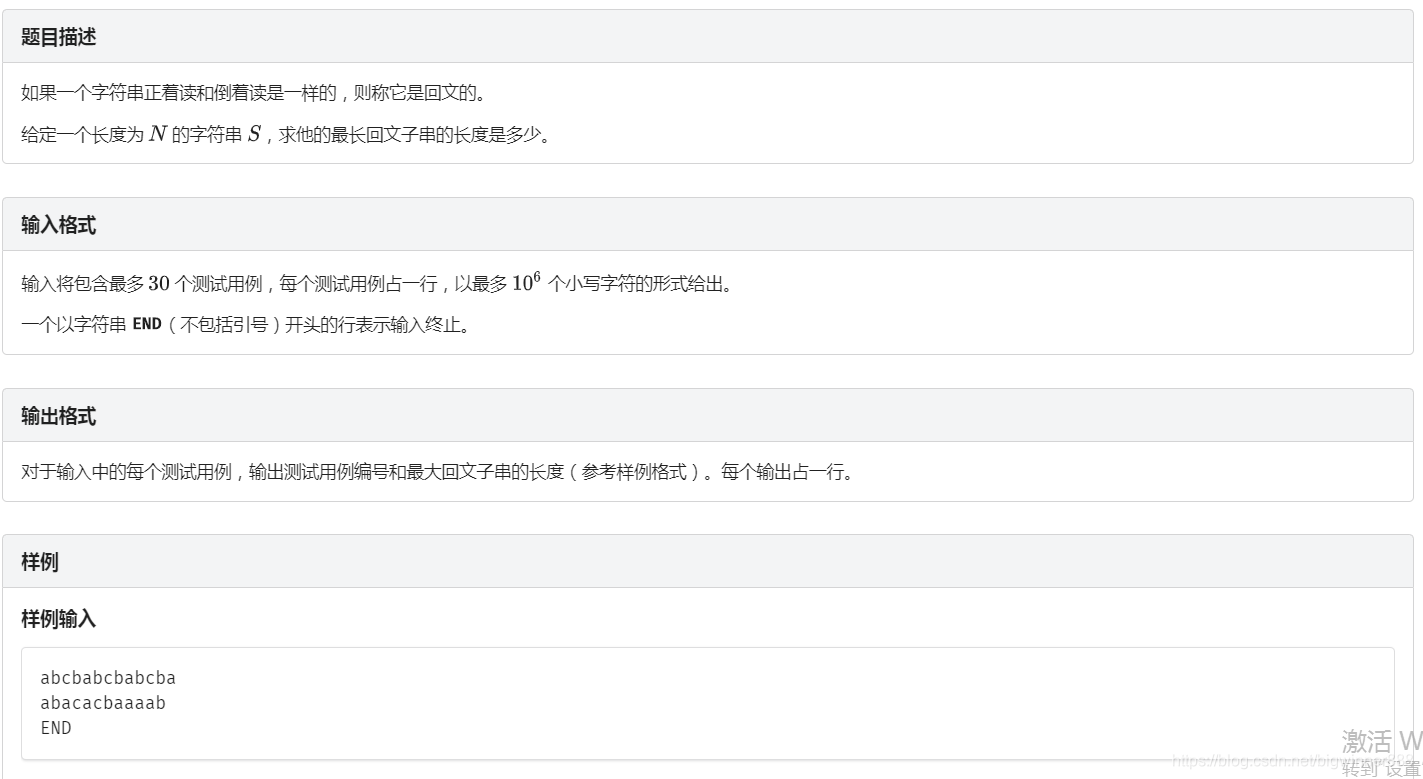

思路:
我们考虑采用二分,
求出回文子串的的一边的长度。
首先用hash函数预处理出每一段字符串的hash值。
接着关心二分的分类讨论:
-
奇回文串A[1~m],其中M为奇数,
并且A[ 1 ∼ M + 1 2 1\sim\frac{M+1}2 1∼2M+1] = reverse(A[ M + 1 2 + 1 ∼ m \frac{M+1}2+1 \sim m 2M+1+1∼m]).
(reverse(A)表示把字符串A倒过来) -
偶回文串A[ 1 ∼ m 1 \sim m 1∼m], 其中M为偶数,
并且A[ 1 ∼ M 2 1 \sim \frac{M}2 1∼2M] = reverse( A [ m 2 + 1 ∼ m ] A[\frac{m}2+1 \sim m] A[2m+1∼m]).
#include<cstdio>
#include<cstring>
#include<iostream>
#define ull unsigned long long
using namespace std;
int n, l, r, mid, ans, number;
ull times[1000002], zheng[1000002], fan[1000002];
char c[1000002];
int main()
{
scanf("%s", c + 1);
n = strlen(c + 1);
while (c[1] != 'E' || c[2] != 'N' || c[3] != 'D')
{
number++;
ans = 1;
memset(times, 0, sizeof(times));
memset(zheng, 0, sizeof(zheng));
memset(fan, 0, sizeof(fan));
times[0] = 1ull;
for (int i = 1, j = n; i <= n, j >= 1; i++, j--) //预处理
{
times[i] = (times[i - 1] * 131ull);
zheng[i] = (zheng[i - 1] * 131ull + c[i] - 'a');
fan[j] = (fan[j + 1] * 131ull + c[j] - 'a');
}
for (int i = 1; i <= n; i++)
{
l = 0;
r = n;
while (l <= r)
{
mid = (l + r) >> 1;
if (i - mid < 1 || i + mid > n) //奇数回文
{
r = mid - 1;
continue;
}
if (zheng[i] - zheng[i - mid - 1] * times[mid + 1] == fan[i] - fan[i + mid + 1] * times[mid + 1])
{
l = mid + 1;
ans = max(ans, mid * 2 + 1);
}
else r = mid - 1;
}
l = 0;
r = n;
while (l <= r) //偶数回文
{
mid = (l + r) >> 1;
if (i - mid + 1 < 1 || i + mid > n)
{
r = mid - 1;
continue;
}
if (zheng[i] - zheng[i - mid] * times[mid] == fan[i + 1] - fan[i + mid + 1] * times[mid])
{
l = mid + 1;
ans = max(ans, mid * 2);
}
else r = mid - 1;
}
}
printf("Case %d: %d\n", number, ans);
memset(c, 0, sizeof(c));
scanf("%s", c + 1);
n = strlen(c + 1);
}
return 0;
}
随便自己在网上看到了一篇题解,
讲到了著名的马拉车算法,大家可以去康康。
例题三:对称正方形link


思路:
首先,很明显要用 hash 来做,
因为是矩形,是二维的。
那就要用二维的 hash。
现在来讲一下二维hash:
一维hash是把一个字符串或一个序列用一个整数表示。
二维hash则是把一个矩阵用一个整数表示。
我们两次 H a s h Hash Hash ,第一次,我们横着 H a s h Hash Hash :
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
hash[i][j] = hash[i][j - 1] * base_1 + a[i][j];
此时的 H a s h ( i , j ) Hash(i, j) Hash(i,j) 表示第 i i i 行第 j j j 个数的 H a s h Hash Hash 值,
此时我们进行第二次 H a s h Hash Hash :
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
hash[i][j] = hash[i - 1][j] * base_2;
若我们要查询左上角为 ( x , y ) (x, y) (x,y) ,
右下角为 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 的矩阵的 H a s h Hash Hash值就为:
h a s h ( x 1 , y 1 ) − h a s h ( x − 1 , y 1 ) ∗ b a s e 2 x 1 − x + 1 − h a s h ( x 1 , y − 1 ) ∗ b a s e 1 y 1 − y + 1 + h a s h ( x − 1 , y − 1 ) ∗ b a s e 2 x 1 − x + 1 ∗ b a s e 1 y 1 − y + 1 hash(x_1,y_1)-hash(x-1, y_1) * base_2^{x_1-x+1}-hash(x_1,y-1)*base_1^{y_1-y+1}+hash(x-1,y-1)*base_2^{x_1-x+1}*base_1^{y_1-y+1} hash(x1,y1)−hash(x−1,y1)∗base2x1−x+1−hash(x1,y−1)∗base1y1−y+1+hash(x−1,y−1)∗base2x1−x+1∗base1y1−y+1
o k ok ok ,回到正题。。。
那你考虑一下一个左右上下对称的正方形要满足什么特点。
那很明显,对称就是按着对称轴翻转过来它还是一样的。
那就是这个正方形左右反过来,
上下反过来所形成的图形和原来都一样。
那你就构造出最大的矩形的两个翻转图形,
然后看看原来的位置应该变道哪里。
原来是 [ x , y ] [x,y] [x,y] (假设),
那左右翻转就是 [ x , m − y + 1 ] [x,m−y+1] [x,m−y+1] ,
上下翻转就是 [ n − x + 1 , y ] [n−x+1,y] [n−x+1,y] 。
那我们再看矩形翻转之后的位置变化。
假设原来是 [ l x , l y ] ∼ [ r x , r y ] [lx,ly]\sim[rx,ry] [lx,ly]∼[rx,ry] ,
那左右翻转的就是 [ l x , m − r y + 1 ] ∼ [ r x , m − r x + 1 ] [lx,m-ry+1]\sim[rx,m-rx+1] [lx,m−ry+1]∼[rx,m−rx+1] ,
上下翻转的就是 [ n − r x + 1 , l y ] ∼ [ n − l x + 1 , l y ] [n-rx+1,ly]\sim[n-lx+1,ly] [n−rx+1,ly]∼[n−lx+1,ly] 。
依题意,
得出一个结论:当一个正方形合法时,
以这个正方形的中心且比它小的正方形也合法,
故我们可以枚举中心点,
二分出最大的合法正方形的边长 L L L ,
贡献为 [ L + 1 2 ] [\frac{L+1}2] [2L+1] ,
接着考虑到中心点不一定是矩阵中的数,
我们需要进行两次遍历。
最后的答案还得加上 n ∗ m n * m n∗m
#include<cstdio>
#include<iostream>
#define di1 1000000007ull
#define di2 1000000009ull
#define ull unsigned long long
using namespace std;
int n, m, a[1001][1001], matrix_up[1001][1001], matrix_left[1001][1001], l, r, mid, ans, tot, lx, ly, tmp;
ull hash[1001][1001], times1[1001], times2[1001], hash_up[1001][1001], hash_left[1001][1001], hash1, hash2, hash3;
bool ch(int rx, int ry, int dis)
{
lx = rx - dis + 1;
ly = ry - dis + 1;
hash1 = hash[rx][ry] - hash[rx][ly - 1] * times1[dis] - hash[lx - 1][ry] * times2[dis] + hash[lx - 1][ly - 1] * times1[dis] * times2[dis];
tmp = rx;
rx = n - (rx - dis);
lx = rx - dis + 1;
ly = ry - dis + 1;
hash2 = hash_up[rx][ry] - hash_up[rx][ly - 1] * times1[dis] - hash_up[lx - 1][ry] * times2[dis] + hash_up[lx - 1][ly - 1] * times1[dis] * times2[dis];
rx = tmp;
ry = m - (ry - dis);
lx = rx - dis + 1;
ly = ry - dis + 1;
hash3 = hash_left[rx][ry] - hash_left[rx][ly - 1] * times1[dis] - hash_left[lx - 1][ry] * times2[dis] + hash_left[lx - 1][ly - 1] * times1[dis] * times2[dis];
if (hash1 == hash2 && hash1 == hash3) return 1;
return 0;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
matrix_up[n - i + 1][j] = a[i][j];
matrix_left[i][m - j + 1] = a[i][j];
}
times1[0] = times2[0] = 1ull;
for (int i = 1; i <= n; i++) times1[i] = times1[i - 1] * di1;
for (int i = 1; i <= m; i++) times2[i] = times2[i - 1] * di2;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
hash[i][j] = hash[i][j - 1] * di1 + a[i][j];
hash_up[i][j] = hash_up[i][j - 1] * di1 + matrix_up[i][j];
hash_left[i][j] = hash_left[i][j - 1] * di1 + matrix_left[i][j];
}
times1[i] = times1[i - 1] * di1;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
hash[i][j] += hash[i - 1][j] * di2;
hash_up[i][j] += hash_up[i - 1][j] * di2;
hash_left[i][j] += hash_left[i - 1][j] * di2;
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
ans = 0, l = 1, r = min(min(i, n - i + 1), min(j, m - j + 1));
while (l <= r)
{
mid = (l + r) >> 1;
if (i - mid + 1 < 1 || i + mid - 1 > n || j - mid + 1 < 1 || j + mid - 1 > m)
{
r = mid - 1;
continue;
}
if (ch(i + mid - 1, j + mid - 1, mid * 2 - 1)) ans = mid, l = mid + 1;
else r = mid - 1;
}
tot += ans;
ans = 0, l = 1, r = min(min(i, n - i), min(j, m - j));
while (l <= r)
{
mid = (l + r) >> 1;
if (i - mid + 1 < 1 || i + mid > n || j - mid + 1 < 1 || j + mid > m)
{
r = mid - 1;
continue;
}
if (ch(i + mid, j + mid, mid * 2)) ans = mid, l = mid + 1;
else r = mid - 1;
}
tot += ans;
}
printf("%d", tot);
return 0;
}
例题四:单词背诵link


思路:
这道题思路比较简单,只用将要背单词用hash存储信息,
然后我们在后来的操作中进行匹配就行了。
那具体操作呢?
考虑使用尺取法。
类似毛毛虫爬动,时间复杂度可以得到O(n)的好成绩。
尺取法:顾名思义,像尺子一样取一段,借用挑战书上面的话说,尺取法通常是对数组保存一对下标,即所选取的区间的左右端点,然后根据实际情况不断地推进区间左右端点以得出答案。尺取法比直接暴力枚举区间效率高很多,尤其是数据量大的时候,所以说尺取法是一种高效的枚举区间的方法,是一种技巧,一般用于求取有一定限制的区间个数或最短的区间等等。当然任何技巧都存在其不足的地方,有些情况下尺取法不可行,无法得出正确答案,所以要先判断是否可以使用尺取法再进行计算。
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ull unsigned long long
#define mi 131ull
using namespace std;
struct hhash {
ull hash;
int num;
}hash[1001];
int n, m, size, ans, place[100001], l, r, mid, num, in[1001], answer;
char rem[1001][14], pas[100001][14];
bool have[1001];
ull thash;
bool cmp(hhash x, hhash y) {
return x.hash < y.hash;
}
int getplace() {//通过二分找到要背的单词种是否有这个 hash 值
l = 0;
r = n;
while (l <= r) {
mid = (l + r) >> 1;
if (hash[mid].hash > thash) {
r = mid - 1;
}
else if (hash[mid].hash < thash) l = mid + 1;
else return hash[mid].num;
}
return -1;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", &rem[i]);
size = strlen(rem[i]);
hash[i].num = i;//记录原有的位置
hash[i].hash = rem[i][0] - 'A' + 1;
for (int j = 1; j < size; j++)
hash[i].hash = hash[i].hash * mi + rem[i][j] - 'A' + 1;//得到hash值
}
sort(hash + 1, hash + n + 1, cmp);//排序,让后面可以二分查找是否是这个字符串
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%s", &pas[i]);
size = strlen(pas[i]);
thash = pas[i][0] - 'A' + 1;
for (int j = 1; j < size; j++)
thash = thash * mi + pas[i][j] - 'A' + 1;
place[i] = getplace();
if (place[i] != -1 && !have[place[i]]) {
ans++;
have[place[i]] = 1;
}
}
printf("%d\n", ans);
if (!ans) {
printf("0");
return 0;
}
l = 1;
answer = 2147483647;//尺取法得到最小长度
for (int i = 1; i <= m; i++) {
if (place[i] != -1) {
if (!in[place[i]]) {
num++;
}
in[place[i]]++;
if (num == ans) {
while (l <= i && num == ans) {
if (place[l] != -1) {
in[place[l]]--;
if (!in[place[l]]) {
num--;
answer = min(answer, i - l + 1);
}
}
l++;
}
}
}
}
printf("%d", answer);
return 0;
}
例题五:子正方形 link

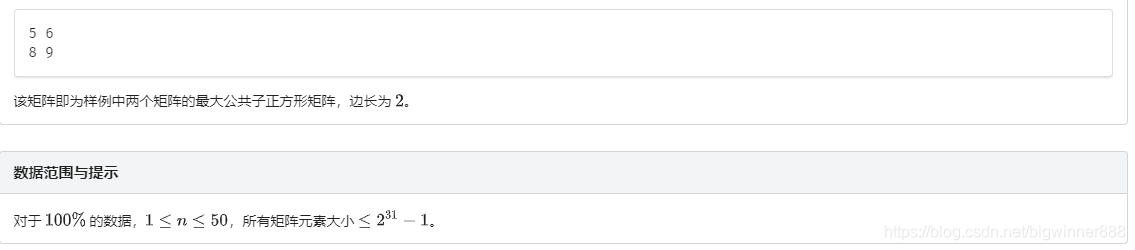
思路:
考虑将二维矩阵求出hash值,
早在例三时讲过,
这里就不在赘述了。
记得在最大正方形中讲过然后在一个矩阵中枚举正方形。
此题类似,
考虑分别在模式矩阵和匹配矩阵中枚举正方形右下角,
比较两者矩阵范围,
求出最大的正方形边长,即:
m
i
n
(
m
i
n
(
s
x
,
t
x
)
,
m
i
n
(
s
y
,
t
y
)
)
min(min(sx, tx) , min(sy, ty))
min(min(sx,tx),min(sy,ty))
接着考虑用二分求出最大可行边长,
最后与final_ans取较大值输出。
#include <cstdio>
#include <iostream>
#define ull unsigned long long
#define base 131ull
#define base1 13331ull
using namespace std;
const int N = 60;
int n, a[N][N], b[N][N], ans, final_ans;
ull hash_a[N][N], hash_b[N][N], t1[N], t2[N];
bool check(int sx, int sy, int tx, int ty, int mid)
{
return
(hash_a[sx][sy] - hash_a[sx][sy - mid] * t1[mid] - hash_a[sx - mid][sy] * t2[mid] + hash_a[sx - mid][sy - mid] * t1[mid] * t2[mid])
==
(hash_b[tx][ty] - hash_b[tx][ty - mid] * t1[mid] - hash_b[tx - mid][ty] * t2[mid] + hash_b[tx - mid][ty - mid] * t1[mid] * t2[mid])
;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
scanf("%d", &a[i][j]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
scanf("%d", &b[i][j]);
t1[0] = t2[0] = 1ull;
for(int i = 1; i <= n; i++) t1[i] = t1[i - 1] * base, t2[i] = t2[i - 1] * base1;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
hash_a[i][j] = hash_a[i][j - 1] * base + a[i][j];
hash_b[i][j] = hash_b[i][j - 1] * base + b[i][j];
}
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
hash_a[i][j] += hash_a[i - 1][j] * base1;
hash_b[i][j] += hash_b[i - 1][j] * base1;
}
for(int sx = 1; sx <= n; sx++)
for(int sy = 1; sy <= n; sy++)
for(int tx = 1; tx <= n; tx++)
for(int ty = 1; ty <= n; ty++)
{
int l = 0, r = min(min(sx, tx) , min(sy, ty)), mid;
ans = 0;
while(l <= r)
{
mid = (l + r) >> 1;
if(check(sx, sy, tx, ty, mid)) ans = mid, l = mid + 1;
else r = mid - 1;
}
final_ans = max(final_ans, ans);
}
printf("%d\n", final_ans);
return 0;
}























 1220
1220

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








