欧拉角(Euler angles)

前言：本人也就英语4级水平，由于本篇中存在大量学术词汇，翻译时必然会有不当之处，原文可以在下面的链接中找到，具体意义各位可以自行斟酌

标红的部分是已发现存疑的翻译，也请各位指正。

维基百科-欧拉角

欧拉角

  欧拉角是由Lenhard Euler引入的，用于描述刚体方向的三个角， 在3维欧几里得空间中描述这样一个方向，需要三个参数。它们（这种方向）可以多种形式给出 , 欧拉角便是它们中的一种; 在 charts on SO(3)中，你可以找到其它的描述方式 . 欧拉角也可以用于描述一个参照系  (通常是一个坐标系 ) 和另一个参照系之间的位置关系. 这三个角通常被定义为  α ,  β ,  γ , 或者  φ ,  θ ,  ψ .

  欧拉角代表一系列的三维基本旋转， 也就是围绕一个坐标系的各轴的一系列旋转。例如，首先绕Z轴旋转一个α角，然后绕x轴做一个β角的旋转，最后再绕Z轴来一个γ角的旋转。这些旋转都是从一个已知的标准方向上进行的。在物理中，

这个初始化的标准方向通常是一个静止的坐标系，在线性几何中，通常是一个标准基。

  任何一个方向都可以使用三个方向的基本旋转描述出来，一个基本旋转既可以是一个绕着固定坐标系中的轴的旋转，也可以是一个

绕着初始时与固定坐标系对齐的，目前正在旋转的坐标系的轴的旋转。（老外这里翻译成中文比较晦涩，实际上就是这个基本旋转

可以是从初始状态绕一个轴进行的旋转，也可以是在一个已经做过一个或几个方向旋转后的坐标系的基础上，再附加的，绕这个旋转

过了的坐标系轴的旋转），每次基本旋转，都会影响这个方向。这个正在旋转的坐标系可以被想象成严格附着在一个刚体上。因此，

它有些时候被称作本地坐标系。不考虑两种不同的旋转轴（内旋或外旋，后续会提及到）定义的话，这里有12种绕轴旋转的方式，被划分为两组：

• Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)
• Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

Tait–Bryan 角也被称作 万向节角（Cardan angles）， 航海角（nautical angles），前进方向(heading), 海拔(elevation), 和 倾斜(bank) 或 偏航(yaw),

俯仰(pitch), 翻滚（roll）。有时候，这两种系列的旋转都叫做“欧拉角”,而第一组中的旋转方式也可以被称为 原始 或 经典 欧拉角。

经典欧拉角

经典定义

欧拉角是在空间中 描述从一个用于表示某个固定的参考系的、已知的方向，经过一系列基本旋转得到、新的代表另一个参考系的方向的方式。

这个方向可以被想成从一个初始的方向，旋转到其确切位置的方向。如下图中描述，原始的参考系的坐标轴被定义为x,y,z,旋转后的坐标系

的坐标轴被定义为X,Y,.在几何和物理中，被旋转的坐标系通常被想象成严格附着在一个刚体上。因此，它被称为一个“本地”坐标系，这也意味着

它既代表这个刚体的位置，也代表这个刚体的方向。

欧拉角的几何定义是基于上面提及的（原始的和经过旋转的）的参考系的坐标轴和一个附加的、被称作 交轨线 的轴做出的。

交轨线（N）是xy和XY坐标平面相交处的一条线。换句话说，这条线，穿过这两个坐标系原点，并且垂直于zZ平面，这三个

欧拉角被如下定义：

• α (or ) x轴和N轴之间的角度。
• β (or ) z轴和Z轴之间的角度。
• γ (or ) N轴和X轴之间的角度。

  
  

上面的定义含义如下

• α 代表绕z轴的旋转,
• β 代表绕N轴的旋转,
• γ 代表绕Z轴的旋转.

  
  

如果β是0, 就没有绕N轴的旋转. 因此Z轴与z轴重合, α 和 γ 代表绕同一个轴(z)的旋转, 最终的方向可以通过一个单一的绕z轴的旋转获得，这个旋转角度等于 α+γ .

可选择的定义方式

经过旋转的参考系XYZ可以被想象成一个在经过欧拉角旋转之前原本与xyz对齐。

其连续的方向变化可以被定义为：

• x-y-z, or x₀-y₀-z₀ (初始转改)
• x’-y’-z’, or x₁-y₁-z₁ (经过第一次旋转)
• x″-y″-z″, or x₂-y₂-z₂ (经过第二次旋转)
• X-Y-Z, or x₃-y₃-z₃ (经过第三次旋转的最终状态)

从上边列出的一系列旋转可以看出，交轨线N可以被简单的定义为经过第一次旋转后的X轴所在的位置，所以，N可以被简单的定义为x'。

而且，由于第三次的基本旋转是绕Z轴进行的，它不会改变Z轴的方向，所以Z轴和z''是重合的，这就可以帮助我们把欧拉角简化为如下形式：

• α (or ) 代表绕z轴的旋转
• β (or ) 代表绕x’轴的旋转,
• γ (or ) 代表绕 z″轴的旋转.

约定

不同的作者可能会使用不同绕轴旋转的去定义欧拉角，或者使用不同的名字去命名相同的角，所以任何关于使用论欧拉角的讨论都要以他们的定义方式为先导。

除非另作说明，这篇文章将使用上面的约定。

三个基本旋转可以发生在初始坐标系的固定的坐标系的xyz轴，也可以发生在正在旋转中的XYZ坐标系的坐标轴上。

有6种为原始欧拉角选择旋转轴的方式。下面中的 1 和 6是相同的。可供选择的方式是

1. z-x’-z″ (内旋) 或 z-x-z (外旋)
2. x-y’-x″ (内旋) 或 x-y-x (外旋)
3. y-z’-y″ (内旋)或 y-z-y (外旋)
4. z-y’-z″ (内旋)或 z-y-z (外旋)
5. x-z’-x″ (内旋)或 x-z-x (外旋)
6. y-x’-y″ (内旋)或 y-x-y (外旋)

欧拉角的定义必须基于两个相同手参考系。

标志和范围

旋转角通常根据右手坐标系进行定义。换句话说，向坐标轴的正方向看去时，一个顺时针的旋转的角度是正值，逆时针时的旋转的角度是负值。

左手坐标系的约定一般很少采用。

关于阈值：

  对于α 和 γ, 范围是2 π的模. 一个合法的范围可能如: [−π, π].

  对于 β, 范围包含π (但是不能说是π的模). 例如可以是 [0, π] 或者[−π/2, π/2]. 

角 α, β 和 γ 一般都是单独取值的，有一种例外情况，那就是xy平面和XY平面重合的情况，z轴和Z轴拥有相同的方向或者相反的方向。

实际上，如果z轴和Z轴相同，β = 0 并且 只有(α + γ)是一个特殊的定义（不是两个独立的值），并且，相似的，如果z轴和Z轴如果是方向相反，

β = π和 (α − γ) 是个特殊的定义（不是两个独立的值）。这种情况在应用中被称作“万向节锁”。

几何推导

获取一个给定参考系的欧拉角最快的方式是 把给出的三个向量写到矩阵中并且与给定的矩阵对比（相关矩阵稍后会在表格中列出）

所以欧拉角是可以被计算出来的，不过，我们可以使用几何推导而不用使用矩阵代数也可以计算出相同的结果，假设一个用单位向量定义的参考系（X,Y,Z）就像下面的图表中

所示

可以看出：

并且由于

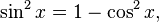
我们有

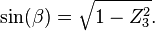
由于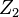是单位向量在双重投影，所以有

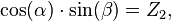
相应的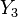也可以类似的得出，

先向z轴和交轨线构成的平面进行投影，因为Y轴和这个平面的角度为且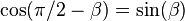，可以导出：

最后可用反cosine函数可得

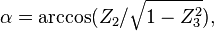
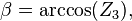
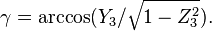
有趣的是反consine函数都可以获得两个可能的值，从几何的角度来看，只有一个答案才是合法的

当欧拉角被定义成一系列的旋转，所有的答案都可能是合法的，但是但是只有一个是符合旋转顺序的。这是因为如果旋转顺序不事先确定的话，得到结果参考系

的旋转序列并不是唯一的。

为了计算，使用atan2(y,x)去表示角可能会更有用。

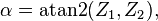
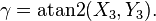
泰特-布莱恩角

Tait–Bryan angles. z-y′-x″ sequence (intrinsic rotations; N coincides withy’)

（Tail-Bryan角。z-y'-x''顺序， 序列（内旋; N 与 y’重合））

欧拉角的第二种表达形式被叫做Tail-Bryan角，在通过Peter Guthrie Tail和Gerge H. Bryan努力之后，Tail-Bryan角的定义和表示与经典欧拉角的表示方法类似。

唯一的不同是 Tail-Bryan角 使用三个轴上的旋转角度去表示。（例如 x-y-z或者x-y'-z''），然而经典欧拉角的第一个旋转角度和第三个旋转角度都是围绕同一个轴的

例如（z-x-z,或者 z-x'-z''）。

这会产生一个不同于经典欧拉角中的交轨线。在经典欧拉角中，这个交轨线是两个相对应的笛卡尔平面的交线，（当欧拉角为0时，平行的两个笛卡尔平面，例如xy和XY平面）。

在第二种情况中Tait-Bryan角中，它是两个不对应的平面的交线（当欧拉角为0时，互相垂直的两个平面，例如：xy和YZ平面）。

约定

基本旋转既可以围绕着原始未移动的坐标系进行(外旋),也可以围绕那些已经经过几次基本旋转的正在旋转的坐标系的轴进行（内旋）。

有6种旋转的顺序可供选择，分别是：

1. x-y’-z″ (内旋) or x-y-z (外旋)
2. y-z’-x″ (内旋) or y-z-x (外旋)
3. z-x’-y″ (内旋) or z-x-y (外旋)
4. x-z’-y″ (内旋) or x-z-y (外旋)
5. z-y’-x″ (内旋) or z-y-x (外旋): 此序列的内旋被叫做: 偏航（绕z旋转）, 俯仰（绕y'旋转） 和 翻滚(绕x''旋转) 
6. y-x’-z″ (内旋) or y-x-z (外旋)

可供选择的命名

泰特-布莱恩角中 z-y'-x''这个序列(内旋) 通常被叫做航海角，因为他们可以用来描述一艘船或者一架飞行棋的方向，或者可以叫做万向角，也可以把这几个

旋转叫做 heading(摆头),elevation(俯仰)和bank(倾斜)，或者叫做 yaw(偏航)，pith(俯仰)和roll（翻滚）。注意第二套叫法也被用在三个飞行器轴中

物理移动关系

内旋

内旋是发生在正在旋转的坐标系中的坐标轴上的旋转

XYZ坐标系旋转，xyz坐标系静止不动，三个内旋可以使XYZ坐标系指向任何一个方向。欧拉角或者泰勒-布莱恩角中(α, β, γ)是这三个旋转的幅度

例如目标方向可以这样抵达：

• XYZ 绕Z轴(初始时与z轴重合的那个轴)旋转角度α. 现在X 轴位于交轨线上.
• XYZ绕现在的X轴角度为β. Z轴现在已经位于其最终的位置, X轴还停留在交轨线上.
• XYZ绕新的Z轴角度为γ

上面提到的变量让我们可以总结出：

    三个基本旋转分别是绕着z,x'，z''进行的。实际上这组旋转经常被叫做z-x'-z''序列。欧拉角和泰勒-布莱恩角中变量命名

一般都是这样的。有时这样的旋转序列也被叫做z-x-z，Z-X-Z，或者是3-1-3，但是这样命名容易与外旋产生分歧，所以有必要

指出是内旋还是外旋。

Any target orientation can be reached, starting from a known reference orientation, using a specific sequence of intrinsic rotations, whose magnitudes are the Euler angles of the target orientation. This example uses the  z-x′-z″sequence.

可以用旋转矩阵表达内旋，例如

如果使用左乘列向量表达这个旋转组合，结果是

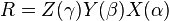
用右乘横向量的表达式和这个是一样的。

外旋

外旋是用围绕固定坐标系xyz的坐标轴的旋转角度进行标识的。 xyz是固定不懂的，而XYZ旋转， 开始时XYZ和xyz是重合的，经过三个绕xyz轴的基本旋转

XYZ可以达到指定的方向。同样 欧拉角或泰勒-布莱恩角中的三个基本旋转的角度也用(α, β, γ进行表示

例如，最终旋转可以用下面的步骤进行表示：

  

• XYZ坐标系绕z轴α. 现在X轴与x轴的角度为α.
• XYZ坐标系再绕x轴β. 现在Z轴与z轴的角度为β.
• XYZ第三次绕z轴旋转γ.

总的来说，上面过程中，这三个基本旋转是围绕z,x,z轴进行的。实际上 这个也经常被定义为z-x-z或者3-1-3，在欧拉角和泰勒-布莱恩角中都是这样命名的

一个用欧拉角表示的旋转 (α,β, γ) = (−60°, 30°, 45°),  z-x’-z″序列 内旋

一个和上图相同的旋转 (γ, β, α) = (45°, 30°, −60°), z-x-z序列 外旋

Any extrinsic rotation is equivalent to 

用旋转矩阵可以表达外旋序列，例如

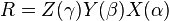
用左乘竖向量的方式可以表达为

右乘横向量的表达式与这个是一致的

万象移动关系

Euler basic motions of the Earth. Intrinsic (green), Precession (blue) and Nutation (red)

欧拉基本移动是通过改变欧拉角中其中一个角，同时保持另外两个角不变而得到的。

欧拉旋转从来不会基于外部参考系，或基于相对旋转的参考系的旋转表示。

但是在某些混合使用的情况下，它们会组成一个混合轴的旋转系统。

如左图，第一个旋转角度使交轨线绕着外部的z轴进行旋转，第二个旋转角度是围着交轨线进行旋转的，第三个旋转角度是个围绕着在体内固定轴移动的内旋。（为何第三个被称为内旋？这里理解有误？）

这些旋转被称作 旋进 点头和内旋（自旋）。举个例子，一个陀螺，这个陀螺绕着自己的对称轴进行旋转，这个对应于他的内旋，同时它还绕着它的中轴进行旋转，这个就叫做旋进。最后，这个陀螺还会上下摆动，这个倾角就叫做它的点头角.这三个分别划分到不同的参考系中，都是一个旋转角。只有旋进是一个合法的旋转操作，并且通常只有旋进可以用一个基于空间的矩阵所表示。（翻译有问题？这个不太理解）

万向节类比

Left: A three axes  z- x- z  gimbal where the external frame and external axis  x are not shown and axes  Yare perpendicular to each gimbal ring.  Right: A simple diagram showing the Euler angles and where the axes  Y of intermediate frames are located.

我们假设有一系列的参考系，可以在之前移动的基础上分别只在一个角度上进行旋转， 类似一个万向节，这里会存在一个外部的固定参考系，一个最终参考系和两个在中间的被叫做“中间参考系”的参考系。这两个像悬浮环的、在中间的参考系可以让最终的参考系达到任何一个方向。

这样，每个欧拉旋转对应一个环，与剩下的环保持独立。

中间参考系

悬浮环表示中间参考系，他们也可以被静态的定义，分别在x,y,z轴上有向量i,j,k，在XYZ上有向量I,J,K，N在交轨线上，一些中间参考系可以用向量叉乘的形式进行定义如下：

• 初始状态: [i,j,k] (k = i × j)
• 第一个参考系: [N,k × N,k]
• 第二个参考系: [N,K × N,K]
• 最终参考系: [I,J,K]

这些中间参考系和那些悬浮环是等价的，其中一个环转动，最终的方向便会产生变动。这证明了：

• 通过组合这三个旋转，原始参考系可以被旋转到与任何一个目标参考系.
• 这些旋转角就是目标参考系的欧拉角.

翻译未完，后续会接着进行翻译，并对内容加深理解，修正文章中的错误翻译。