NLP学习笔记39-神经网络BP算法

最新推荐文章于 2024-04-24 16:26:58 发布

bohu83

最新推荐文章于 2024-04-24 16:26:58 发布

阅读量776

点赞数

分类专栏： NLP 文章标签：神经网络 BP算法反向传播推导

本文链接：https://blog.csdn.net/bohu83/article/details/115419513

版权

NLP 专栏收录该内容

76 篇文章 23 订阅

订阅专栏

一序

本文属于贪心NLP训练营学习系列。上节课学习了神经网络的数学表达，本节学习数学表达式的参数w,b.

二神经网络的损失函数

假设模型有一个输入层，一个输出层以及L个隐含层。我们把softmax作为输出层的激活函数.

我们把output层的pre-Activation部分写作 $a^{(L+1)}(x)$ ，post-Activation 部分写作f(x).

$f(x)= softmax(a^{(L+1)}x )$

损失函数主要部分： $L(f(x^{(t)} ;\theta ),y^{(t)} )$ , 其中参数 $\theta = \{ ( w^{i},b^{i})_{i=1}^{L+1} \}$ 损失函数包含两项是预测值，真实值。

损失函数： $argmin_{\theta }=\frac{1}{T} \sum_t L(f(x^{(t)} ;\theta ),y^{(t)} ) + \lambda \Omega (\theta )$ ，前面的均值函数为经验风险,后面结构风险（可以看做是正则项，为了解决过拟合的问题）。

区分损失函数、代价函数和目标函数之间的区别和联系：

损失函数（Loss Function）通常是针对单个训练样本而言。

代价函数（Cost Function）通常是针对整个训练集。

目标函数（Objective Function）通常是一个更通用的术语，表示任意希望被优化的函数。

三者关系：A loss function is a part of a cost function which is a type of an objective function。

接下来是使用随机梯度下降法SGD求解的过程。

初始化 $\theta =\{ w^1,b^1,....,w^{L+1},b^{L+1} \}$

接下开看函数L怎么表达。

交叉熵损失函数

假设是一个四分类问题，我们可以计算出 f(x)的值，{0.6,0.2,0.1,0.1},我们的真实值y通常用one-hot表示,{0,1,0,0},

那么f(x) 与y的交叉熵= $-( 0* log0.6+ 1* log0.2+ 0*log 0.1+0*log 0.1)=-log0.2$

推广来看，对于任意的f(x),y ， $L(f(x),y) =-logf(x)_y$ ,这里的y是下标。因为对于one-hot方式，只有一个值为1，其余为0.

三 BP算法

损失函数对于要求参数，就是loss对于整个网络每个参数梯度。为了计算梯度，涉及了几个方面的计算。

loss对于output层的post-Activation 部分f(x).对于output层的pre-Activation部 $a^{(L+1)}(x)$ . output层需要特殊处理。

对于隐含层，post-Activation 部分 $h^{(k)}(x)$ ,pre-Activation部分 $a^{(k)}(x)$ .

最后，计算loss对于参数( $w^{k},b^{k}$ )

BP算法的学习过程由正向传播过程和反向传播过程组成。在正向传播过程中，输入信息通过输入层经隐含层，逐层处理并传向输出层。如果在输出层得不到期望的输出值，则取输出与期望的误差的平方和作为目标函数，转入反向传播，逐层求出目标函数对各神经元权值的偏导数（也称梯度），构成目标函数对权值向量的梯量，作为修改权值的依据，网络的学习在权值修改过程中完成。误差达到所期望值时，网络学习结束。

3.1 Gradient Computation of output

由于 $loss(f(x),y)$ 是一个具体的值，而 $f(x)$ 是一个向量，所以我们先考虑一个值.假设是第c个值，则我们先考虑 $f(x)_c$

$\frac{ \partial loss(f(x),y) }{ \partial f(x)_c}= \frac{ \partial -log(f(x)_y) }{ \partial f(x)_c}$

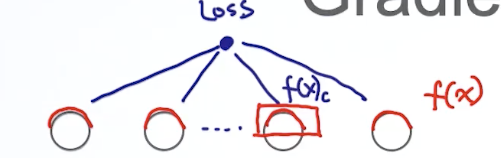
= $\frac{ -1}{ \partial f(x)_c}\cdot \frac{\partial f(x)_y }{\partial f(x)_c }= \frac{ -1 \cdot I(y=c) }{ \partial f(x)_c}$ 其中： $I(y=c) =\left\{\begin{matrix} 1, y=c \\ 0, y\neq c \end{matrix}\right.$

那么

$\frac{ \partial loss(f(x),y) }{ \partial f(x)}= \frac{ \partial -log(f(x)_y) }{ \partial f(x)}= \frac{-1}{ f(x)_y}\cdot \begin{pmatrix} I(y=1) \\ I(y=2) \\ .... \\ I(y=k) \end{pmatrix}= \frac{-e(y) }{ f(x)_y}$

其中 $e(y)$ 采用独热向量编码编码,如果y=1, $e(y)=(1,0,0,...0)$

再计算第二个

$\frac{\partial loss(f(x),y) }{ \partial a^{(L+1)}(x)_c }= \frac{-log(x)_y }{{ \partial a^{(L+1)}(x)_c } }= \frac{-1}{ f(x)_y}\cdot \frac{ \partial }{\partial a^{(L+1)}(x)_c } f(x)_y$

这里output层从 $a^{(L+1)}x$ 到 $f(x)$ 我们当做分类器使用，就是 $f(x)$ 是 $a^{(L+1)}x$ 经过softmax函数的转行.所以我们按照softmax的定义，先把 $f(x)$ 表示出来。

= $\frac{-1}{ f(x)_y}\cdot \frac{ \partial }{\partial a^{(L+1)}(x)_c } \frac{ exp( a^{(L+1) } (x)_y ) }{ \sum_{ c'} exp(a^{(L+1)} (x)_c' )}$

补充一个求导基础运算

$\left ( \frac{ y}{ x} \right )'= \frac{ y'x-x'y }{ x^2}= \frac{ y'}{ x}- \frac{ x'y}{x^2}$

= $\large \frac{ -1}{ f(x)_y}\cdot (\frac{ \frac{ \partial }{\partial a^{(L+1)}(x)_c }exp( a^{(L+1) } (x)_y ) }{ \sum_{ c'} exp(a^{(L+1)} (x)_c') } - \frac{ exp( a^{(L+1) } (x)_y) \cdot \frac{ \partial \sum_{ c'} exp(a^{(L+1) } (x)_c') }{\partial a^{(L+1)}(x)_c } }{ (\sum_{ c'} exp(a^{(L+1) } (x)_c'))^2 } )$ 对照视频拼写了最复杂的式子了，下面进行简化。

= $\large \frac{ -1}{ f(x)_y}\cdot (\frac{exp( a^{(L+1) } (x)_y ) \cdot I(y=c) }{ \sum_{ c'} exp(a^{(L+1)} (x)_c') } - \frac{ exp( a^{(L+1) } (x)_y) \cdot exp(a^{(L+1) } (x)_c') }{ (\sum_{ c'} exp(a^{(L+1) } (x)_c'))\cdot (\sum_{ c'} exp(a^{(L+1) } (x)_c')) } )$ 注意是对 $\large e^x$ 复合函数的求导

= $\frac{-1}{f(x)_y}\cdot(softmax(a^{(L+1)} (x)_y ) \cdot I(y=c) - softmax(a^{(L+1)} (x)_y)\cdot softmax(a^{(L+1)} (x)_c) )$ 利用了softmax函数的定义

= $\frac{-1} {f(x)_y }\cdot ( f(x)_y \cdot I(y=c)-f(x)_y\cdot f(x)_c )$

= $f(x)_c-I(y=c)$

现在我们求出了loss对于out-put层第c个神经元的pre-Activation梯度，同样我们参照上面按照向量表达的方法求解loss对于 $a^{(L+1)}x$ 的梯度

$\frac{\partial loss(f(x),y) }{ \partial a^{(L+1)}(x) }= f(x)-e^{(y)}$

这里的 $e^{(y)}=\begin{pmatrix} I(y=1) \\ I(y=2) \\ .... \\ I(y=k) \end{pmatrix}$

3.2 Gradient Computation of hidden layer

对于隐含层，在做反向传播的时候loss对它的 post-Activation 部分的梯度是依赖于上一层的pre-Activation节点的。

为了求解第K层的梯度，会使用到链式求导方法。

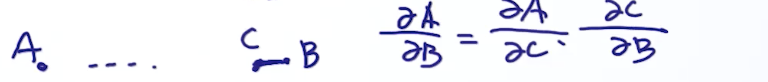
如果计算从A到B的梯度，只途径C点： $\frac{ \partial A }{ \partial B}= \frac{ \partial A }{ \partial C} \cdot \frac{ \partial C }{ \partial B}$

如归途径多个点（ $c_1,c_2,...,c_n$ ）. $\frac{ \partial A}{ \partial B } = \sum _{i=1}^{n} \frac{\partial A }{ \partial C_i} \cdot \frac{\partial C_i }{ \partial B}$

所以， $\frac{ \partial loss(f(x),y)}{ \partial h^{(k)}x_c} = \sum_i \frac{\partial loss(f(x),y) }{ \partial a^{(k+1)}(x)_i} \frac{ \partial a^{(k+1)}(x)_i }{ \partial h^{(k)}x_c }$

根据神经网络的定义： $a^{(k+1)}(x)_i = \sum_j w_{ij}^{(k+1)} \cdot h^{(k)}(x)_j$

= $\sum_i\frac{\partial -logf(x)_y }{ \partial a^{(k+1)}(x)_i} \cdot w_{ij}^{(k+1)}$ 后面的一项，这里当j=c,求导为1.只剩下 $w_{ij}^{(k+1)}$

= $(w_{.j}^{(k+1)} )^T \cdot \frac{\partial -logf(x)_y }{ \partial a^{(k+1)}(x) }$ 把i向量化展开。

上面是只考虑一个神经元的情况。同样对于

$\frac{ \partial loss(f(x),y)}{ \partial h^{(k)} x} = (w^{(k+1)} )^T \cdot \frac{\partial -log f(x)_y }{ \partial a^{(k+1)}x}$

我们再来看隐含层pre-Activation的梯度计算。在做反向传播的时候，它是依赖于post-Activation的。

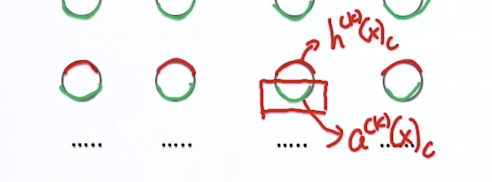
所以根据链式求导方法： $\frac{ \partial loss(f(x),y) }{\partial a^{(k)}(x)_c }= \frac{ \partial loss(f(x),y) }{ \partial h^{(k)}(x)_c}\cdot \frac{ \partial h^{(k)}(x)_c}{ \partial a^{(k)}(x)_c}$

= $\frac{ \partial loss(f(x),y) }{ \partial h^{(k)}(x)_c} \cdot g'(a^{(k)} (x)_c )$ 这里的 $h^{(k) }(x)_c= g(a^{(k)}(x)_c )$

所以

$\frac{ \partial loss(f(x),y) }{\partial a^{(k)}(x)}= (\frac{ \partial loss(f(x),y) }{ \partial h^{(k)}(x)_1}\cdot g'(a^{(k)}(x)_1 ) , \frac{ \partial loss(f(x),y) }{ \partial h^{(k)}(x)_2}\cdot g'(a^{(k)}(x)_2 ) ...)$

这里引入一个概念： $x=(x_1,x_2,x_3)$ , $y=(y_1,y_2,y_3)$ , $x\odot y=(x_1y_1,x_2y_2,x_3y_3)$

这是element-wise product 元素智能乘积。

$\frac{ \partial loss(f(x),y) }{\partial a^{(k)}(x)}= \frac{ \partial loss(f(x),y) }{ \partial h^{(k)}(x)} \odot g'(a^{(k)}(x) )$

3.3 Gradient Computation of parameter

损失函数

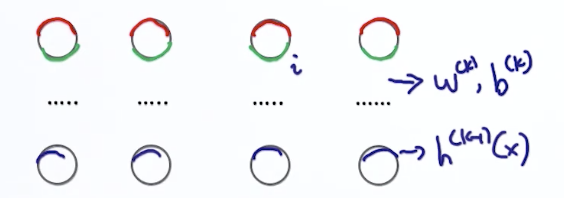
$\frac{ \partial loss(f(x),y) }{ \partial w_{ij}} = \frac{ \partial loss(f(x),y) }{ \partial a^{(k)}x_i } \frac{ \partial a^{(k)}x_i }{\partial w_{ij} }$

根据 pre-Activation 的方程可知 $a^{(k)}(x)_i = \sum_i w_{ij}^{(k)} \cdot h^{(k-1)}x_j$

$\frac{\partial loss(f(x),y) }{ \partial w_{ij}} = \frac{ \partial loss(f(x),y) }{ \partial a^{(k)}x_i } \cdot h^{(k-1)} (x)_j$

同样， $\frac{\partial loss(f(x),y) }{ \partial w} = \frac{ \partial -logf(x)_y }{ \partial a^{(k)}x } \cdot (h^{(k-1)} (x) )^T$

向量展开就是下图的样式

$\frac{ \partial loss(f(x),y) }{ \partial b_{i}^{(k)}} = \frac{ \partial loss(f(x),y) }{ \partial a^{(k)}x_i } \frac{ \partial a^{(k)}x_i }{\partial b_{i}^{(k)} }$

= $\frac{ \partial loss(f(x),y) }{ \partial a^{(k)}x_i }\cdot 1$ 因为b起到的是偏移量，对于求导=1

$\frac{ \partial loss(f(x),y) }{ \partial b^{(k)}} = \frac{ \partial loss(f(x),y) }{ \partial a^{(k)}x } = \frac{ \partial -logf(x)_y }{ \partial a^{(k)}x }$

意思就是BP神经网络中所有参数的梯度，主要是链式求导法则。接下来看怎么吧这些参数套用到BP算法之中。

3.4 BP算法参数更新过程

for training data (x,y)

1 compute output gradient

$\Delta a^{(k+1)}(x)-logf(x)_y= f(x)-e^{(y)}$ 采用独热向量编码编码,如果y=1, $e(y)=(1,0,0,...0)$

2 对于隐含层反向循环，就是从k=L+1 ->1

a. compute gradient of parameter

$\Delta w^{k}-logf(x)_y = (\Delta a^{(k)}x -logf(x)_y ) (h^{(k-1)}(x) )^T$

$\Delta b^{k}-logf(x)_y = (\Delta a^{(k)}x -logf(x)_y )$

b. compute gradient of hidden layer

$\Delta h^{(k-1)}(x)-logf(x)_y =(w^{(k)})^T \cdot ( \Delta a^{(k)}-logf(x)_y )$

$\Delta a^{(k-1)}(x)-logf(x)_y = ( \Delta h^{(k-1)}-logf(x)_y )\odot g'(a^{(k-1)}x)$

**************

如同网上的很多文章，对于BP算法的介绍，更倾向于列公式，尤其是数学不好跟我这种就晕了。有些背景知识就是神经元的分层，输入层、输出层、隐含层通常怎么处理。

权值矩阵w 行列的意义，行代表着这一层有多少个神经元，列代表上一层的输出向量的维度。矩阵好处是element-wise product方便。

再就是要理解BP算法的流程。不是上来就看反向传播，正向传播的流程也要理解,正向传播就是将一个样本 $x_n$ 输入到神经网络，从而获得输出值的过程，参见上面截图，目的是为了保存下各种中间变量 $a(x),h(x),f(x)$ (过程就是不断将输入做线性组合，再应用激活函数，转换成输出，再到下一层的输入，不断重复直到到达神经网络的最后一层）。

反向过程是先计算出out-put层的梯度，再逐层计算隐含层的参数，再计算隐含层的梯度。

最后才是BP算法的数学推导过程。

四 Gradient checking

由于在BP算法中网络比较复杂，参数比较多，如果写错参数经过多层网络会带来比较大影响。如果使用TensorFlow或者pytouch这种三方框架时，它们已经帮我们集成了这个技巧。我们自己手动实现时，通常会使用gradient checking来防止写错参数带来的影响。

利用导数（梯度）的定义：

$f'(x)= \frac{ \partial f(x)}{\partial x } = \frac{ f(x+ \epsilon )- f(x-\epsilon ) }{ 2\epsilon }$

当 $\epsilon$ 很小->0,如果我们用导数定义跟我们实际公式求出的差小于阈值时，我们就认为导数是正确的

bohu83

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
NLP学习笔记39-神经网络BP算法

一序本文属于贪心NLP训练营学习系列。上节课学习了神经网络的数学表达，本节学习数学表达式的参数w,b.二神经网络的损失函数假设模型有一个输入层，一个输出层以及L个隐含层。我们把softmax作为输出层的激活函数.我们把output层的pre-Activation部分写作，post-Activation 部分写作f(x).损失函数主要部分：, 其中参数损失函数包含两项是预测值，真实值。损失函数： ,后面可以看做是正则项，为了解决过拟合的问题。接下来是使用随机梯度下...
复制链接

扫一扫