多边缘至车载雾卸载协议

面向多边缘至多车载雾低成本卸载的去中心化配置协议

摘要

车载雾（VF）系统作为一种新兴平台，由具备计算资源的电动车组成，而这些资源大多未被充分利用。本文考虑一种双层联邦边缘与车载雾（EVF）系统，其中边缘系统可将部分用户流量卸载至附近的虚拟功能，以实现潜在的成本降低。卸载配置旨在确定卸载流量的比例和目标，以实现最大成本降低，本文将其建模为一个混合整数规划问题。我们首先提出一种去中心化卸载配置协议(DOCP)，使单个边缘计算节点ei能够建立自身的卸载配置。随后，我们提出一种多个边缘系统之间的匹配协议，以解决当多个系统同时向同一虚拟功能请求资源时产生的资源争用问题。仿真结果表明，所提出的方法能够利用边缘系统与虚拟功能之间在成本与容量上的异构性。该协议相较于贪婪方法性能最高提升达40%，且与基于粒子群优化的集中式离线方法相当。

索引术语

移动边缘计算，匹配，网络优化，卸载，车载雾。

I. 引言

COMPUTATION 卸载是将计算任务从一个平台转移到另一个平台。在云计算范式中，资源受限的电池供电移动设备可将计算密集型任务卸载到云数据中心，以加速计算、节省电池能量，并规避设备在计算能力和资源容量方面的限制 [1]。然而，云服务提供商可能会对移动设备使用的云资源进行收费。卸载本身也可能带来通信开销，例如额外延迟和能耗，当卸载流量通过无线信道传输时，这些问题可能成为主要关注点。

稿件于2020年8月9日收到；2020年11月10日修订；2020年12月5日接受。出版日期2020年12月23日；当前版本日期2021年2月12日。本工作部分由台湾科技部项目编号108‐2221‐E‐009‐048资助，部分由 H2020合作欧洲/台湾研究项目5G‐CORAL在项目编号761586下资助。

本文的审阅由Z. Fadlullah博士协调。（通讯作者：颜李兴）颜李兴、胡瑞忠和林英达均隶属于台湾新竹30010国立交通大学计算机学院计算机科学系（电子邮件：lhyen@cs.nctu.edu.tw； tony84822@gmail.com；ydlin@cs.nctu.edu.tw）。卡纳亚克·卡尔隶属于台湾台北10607台湾科技大学计算机科学与信息工程系（电子邮件：bkar@mail.ntust.edu.tw）。数字对象标识符 10.1109/TVT.2020.3046874

边缘计算，或更具体地说，多接入边缘计算（MEC），在无线网络边缘提供云服务[2]。与云计算相比，MEC显著降低了服务器与终端设备之间的通信延迟[3]。然而，MEC服务器通常比云数据中心的资源更少，因此单个MEC系统可能没有足够的容量来满足所有服务请求。这就需要在MEC服务器之间进行卸载（即横向卸载）以及在MEC服务器与云数据中心之间进行卸载（即纵向卸载）。

在纵向卸载中，MEC服务器仅在必要时将任务卸载到云，因为云中的任务执行通常会导致更高的端到端延迟。如何选择卸载任务以在满足延迟约束且MEC资源容量有限的情况下最小化总成本，是一个优化问题。

电动汽车和信息通信技术（ICT）的最新进展推动了车联网（IoV）[4]的发展。在车联网（IoV）中，车辆不仅用于交通运输，还作为通信与计算基础设施的一部分。车辆雾计算（VFC）[5]是一种新兴技术，可进一步将车辆转变为雾节点，使其自身及其他连接设备能够作为小规模云平台使用。车辆雾计算（VFC）适用于自动驾驶和导航等应用。然而，当车辆处于停车状态时，该平台通常会关闭，而这些资源本可以被其他云平台所利用。本文中，一个车辆雾（VF）由一个路侧单元（RSU）及其关联的所有车辆（作为VF节点）组成。路侧单元（RSU）作为VF管理器，负责聚合并调度空闲车辆的资源。

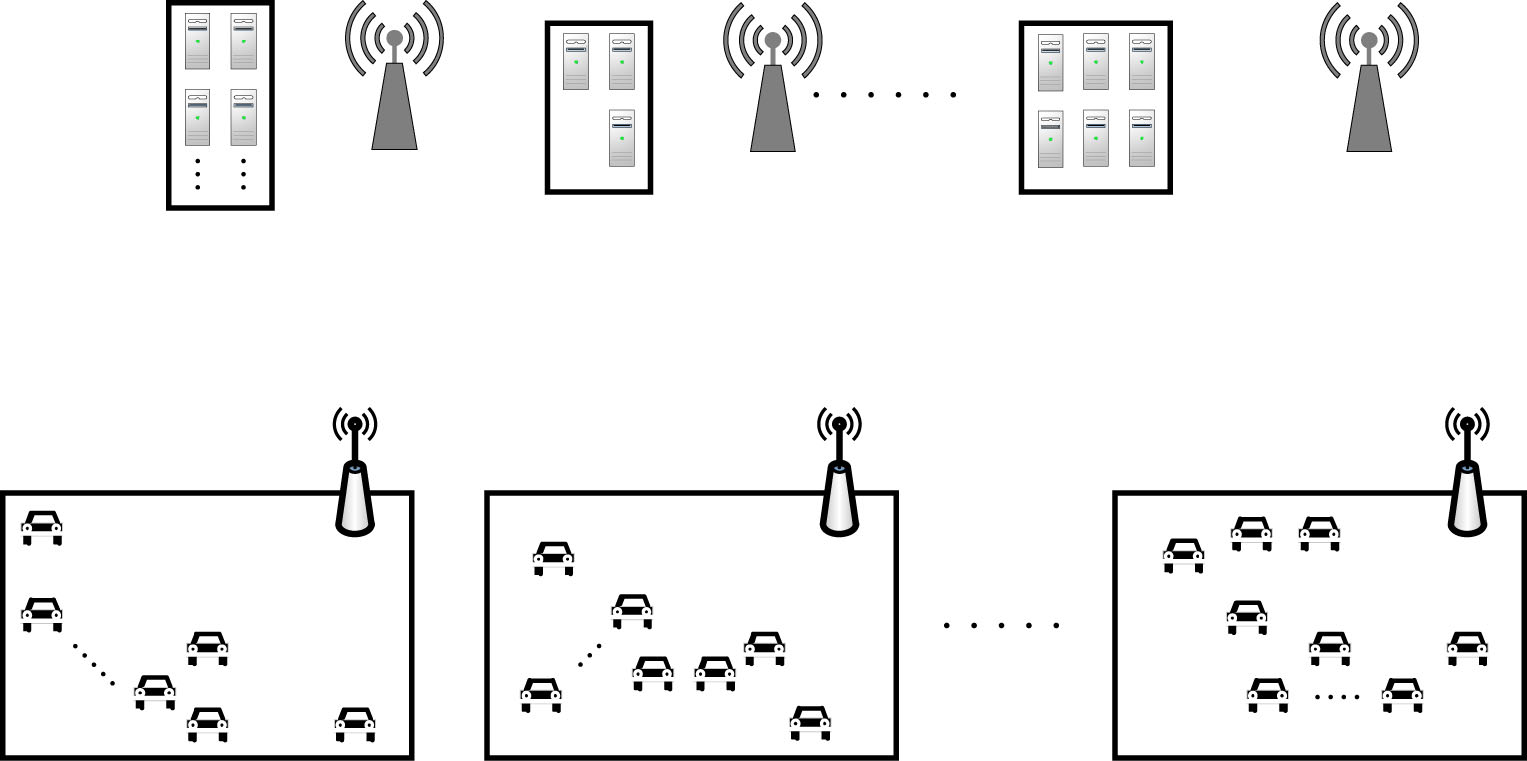
我们考虑将MEC与VF联合形成双层边缘与车辆雾（EVF）架构（图1）。在MEC‐车辆共存场景中，大多数关于计算卸载的研究均考虑将计算任务从车辆向MEC服务器[6],[7]进行卸载以节省能源或获得更强的计算能力。事实上，EVF还支持从MEC系统到VF的纵向卸载。已有研究利用车辆进行卸载，以在交通管理系统[8]中最小化系统响应时间。本研究的核心思想是聚合车辆上原本空闲的资源，分担专用边缘服务器的工作负载，其潜在优势有两方面：一方面，卸载减轻了MEC的资源需求，从而降低了多接入边缘计算系统的运营支出（ OPEX）；另一方面，通过更高效地利用车辆的空闲资源，车主可以获得额外收益。关键在于利用边缘系统与VF之间在成本与容量上的异构性，实现具有成本效益的从MEC到VF的计算卸载。然而，这一潜力尚未得到充分研究。据作者所知，本文的初步版本[9]是唯一研究从边缘系统向VF卸载的工作，但该工作仅考虑了一个边缘系统。本文将[9]扩展至考虑从多边缘向VF的卸载。

当MEC系统接收来自外部的用户请求时，必须决定一种卸载配置，即将用户请求调度到其自身的MEC服务器和选定的VF等执行平台。目标是在满足用户请求的延迟约束以及MEC和VF处理能力的前提下，最小化总成本。由于VF在成本与容量方面具有异构性，最优的卸载配置涉及将流量卸载到多个VF，每个VF承担不同数量的工作负载。通过使用排队模型进行容量和工作负载计算，我们将该优化问题建模为一个混合整数规划问题。然而，我们并不追求该问题的最优解，因为该问题是NP难的，且由于独立MEC服务提供商可能缺乏遵循全局最优结果的动机，全局最优解几乎无法实现。为此，我们提出了一种去中心化卸载配置协议(DOCP)，供各个MEC系统使用，以从每个VF收集容量和成本信息，并基于这些信息自主确定其卸载配置。

DOCP在单MEC EVF环境中表现良好。然而，当多个MEC系统并发执行DOCP以最小化各自成本时，它们的最优配置可能会相互冲突。这需要一种冲突解决机制。我们将无冲突配置集建模为MEC系统与VFs之间的多对多匹配，并在DOCP基础上提出一种去中心化冲突解决协议，该协议借鉴了延迟接受（DA）匹配算法[10],[11]。我们的方法有效地将总体成本最小化目标分解为局部追求收益的子目标。为此，我们为每个MEC系统和每个VF指定一个与收益相关的偏好函数，用以描述其对潜在匹配伙伴的偏好。随着每个参与者追求自身目标，总体成本通常能够得以降低。

我们进行了大量仿真以研究所提出方法的性能。结果表明，所提出的方法能够通过利用多接入边缘计算系统与虚拟功能之间在成本与容量上的异构性，有效降低总成本。与其他替代方案相比，所提出的方法匹配优于倾向于将卸载任务分配给拥有最多车辆数量或最低车辆成本的虚拟功能的贪婪方法。所提出的匹配协议的性能也与粒子群优化算法相当。

总之，本文的主要贡献总结如下。
- 已对电动汽车群系统中从多个多接入边缘计算系统向多个虚拟功能进行计算卸载的总成本最小化问题进行了建模。
- 提出了一种名为DOCP的去中心化卸载配置协议，用于在单个MEC系统中实现低成本卸载配置。
- 在DOCP基础上提出了一种匹配协议，使多个MEC系统能够解决其卸载配置之间的冲突。
- 该冲突解决匹配协议充当了卸载请求方与提供方之间的群体协商机制，确保没有任何请求方可以通过放弃其匹配结果而获得更优收益（这一性质称为个体理性）。

本文的其余部分组织如下。下一节回顾了相关工作，并介绍了EVF系统的计算与通信模型。第三节阐述了成本最小化问题的建模。在第四节中，我们详细介绍了针对单个MEC系统进行卸载配置的DOCP。第五节详细描述了多个MEC系统竞争VF资源的匹配协议。第六节展示了所提出的方法的性能评估以及与其他方案的比较。最后，第七节对本文进行了总结。

II. 背景

A. 相关工作

计算卸载是云计算中以用户为中心的应用场景。一些早期研究致力于用户在计算卸载上的决策 [12],[13]。对于移动边缘计算中的移动设备，用户的决策变量还可能包括计算速度 [14],[15],、信道或带宽接入 [16],[17],、传输功率 [12] 以及卸载流量的比例 [14]。计算卸载的其他问题包括计算资源的分配 [18] 和用户计算任务的调度 [19]。最近，研究人员尝试对卸载决策和资源分配进行联合优化 [20],[21]。

与移动设备类似，雾节点也具有有限的计算能力和资源。一些研究人员提出将计算任务从雾节点卸载到中心云，以减少雾节点的任务执行时间和能耗[22]。Huang等[23]提出了一种基于李雅普诺夫优化的动态卸载算法，在满足移动应用执行时间约束的同时为移动设备节省能耗。在 [24], Liu等中，建模了一个多目标优化问题，以最小化能耗、执行延迟和支付成本。他们提出了一种方法，为每个移动设备寻找最优的卸载概率和发射功率。

利用停车车辆的存储资源这一想法并不新鲜[25]。Hou et al.[5]首次提出将停放和移动的车辆用作雾节点。Wang et al.[8]研究了在车联网（IoV）系统中对实时交通管理工作负载进行卸载的问题。为此，城市被划分为多个区域。在每个区域内设置一个云点，并将附近的停放和移动车辆作为潜在的雾节点以协助卸载任务。在[26],移动设备上运行的时效性强且计算密集型的应用程序被卸载到附近的智能车辆上。当执行卸载任务的车辆由于移动性即将不可用时，该车辆需要将任务移交至另一辆车辆或返回至移动设备。问题在于找出合适的移交时机和目标，以在满足应用程序延迟约束的同时最小化能耗。

Zhou et al.[6]考虑了一种车辆工作负载卸载场景，其中多辆车辆处于单个RSU的覆盖范围内。每辆车的计算工作负载可选择在本地处理或卸载至与RSU共址的边缘服务器。卸载决策通常能为车辆用户带来更高的体验质量，但也会产生费用。对于边缘计算服务提供商而言，卸载带来了收入，但也增加了电力成本。Zhang etal.[27]同样研究了从多辆车辆向多个位于RSU处的车载边缘计算（ VEC）服务器进行卸载的问题。他们将其建模为一个斯塔克尔伯格博弈，并提出了一种分布式算法，以最大化车辆和VEC服务器双方的效用。

Lin et al.[9]提出了首个从边缘卸载到虚拟功能的研究。他们假设了与本文相同的系统模型，但仅考虑了一个边缘系统与多个虚拟功能的情况。在本文中，我们将[9]扩展至考虑从多边缘到多虚拟功能的卸载。

卸载方向	实体数量	研究
车辆→MEC	多车辆→单MEC	[6]
车辆→MEC	多车辆→多MEC	[7]
MEC→车辆	单MEC→多车辆	[9]
MEC→车辆	多MEC→多车辆	本文

表I 车载环境中近期的卸载研究

B. 系统模型

在VFC中有两种类型的虚拟功能。在静态虚拟功能中，车辆停放在大型停车场（例如位于机场或火车站的停车场）数小时甚至数天。尽管车辆仍可能动态加入或离开虚拟机资源池，但频率不高，因此虚拟机资源池的容量不会发生剧烈变化。因此，静态虚拟功能可用于托管区块链应用等计算密集型任务。

在动态虚拟机资源池中，车辆在临时停靠某些地点（例如高速公路休息区）时参与虚拟机资源池。由于动态变化

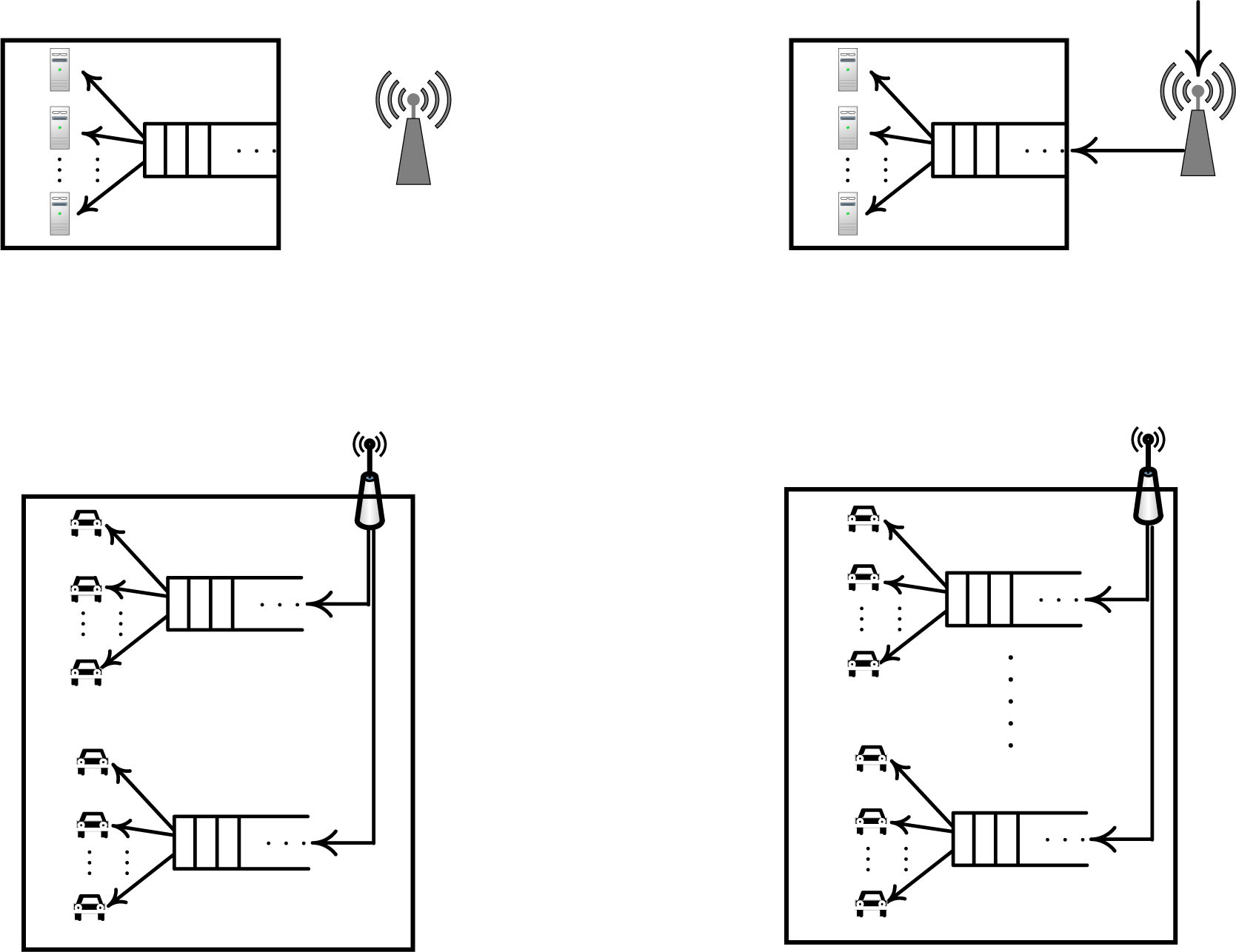
容量，动态虚拟机资源池可能仅托管易于实例化和终止的轻量级任务。在某些区域，动态虚拟机资源池的数量可能足够多，如果能够谨慎且明智地利用这些虚拟功能，我们可以从动态虚拟机资源池中获得可观的资源。

我们考虑如图2所示的从多个MEC系统到多个VF的卸载配置。在这个双层EVF架构中，由外部用户输入到MEC系统的计算工作负载可以部分由MEC系统的服务器处理，部分卸载到VF。同时，一个VF可以服务来自多个MEC系统的卸载请求。

我们假设有MEC系统集合 E={ei} |E| i=1。进入MEC系统 ei的用户请求形成一个泊松过程 Ri，其均值到达速率为 λin i。该工作负载带有延迟约束 Lmax i 。对于每个MEC系统，都有一个流量分流器，根据配置的工作负载分割比例将用户的流量在MEC和VF系统之间进行分配。

每个MEC系统 ei ∈ E拥有ˆmi个同构的MEC服务器。其中， mi ≤ˆmi台服务器将被分配用于处理用户的工作负载。单个MEC服务器在 ei中被建模为一个服务速率为 μi的M/M/1排队系统。因此，将 c台MEC服务器整体分配以先来先服务的方式处理工作负载，相当于构成一个M/M/c队列（如[6]所示）。

我们假设有一组虚拟功能集合 F={fj} |F| j =1，每个对应一个路侧或非路侧停车场。进入停车场的车辆动态被建模为一个 M/M/C[28],[29] 或 M/M/∞ 队列 [30]。我们假设车辆以速率为 aj 的泊松过程加入 VFfj 。车辆在 fj 中的停留时间被假定为均值为 1/dj 的独立同分布的指数随机变量。我们采用 M/M/∞ 模型，因此 fj 中车辆数量服从均值为 aj /dj 的泊松分布。为了利用驻留在虚拟功能中的车辆，我们还应考虑其剩余能量和功耗速率。设 pres j ,k 和 prate j ,k 分别为车辆 k 在虚拟功能 fj 中的剩余能量和功耗速率（均以百分比表示）。如果仅当车辆的剩余能量不低于 pth j ,k% 时才可被利用，则该车辆的最大使用时间为
$$
t_{j,k} = \frac{p_{res}^{j,k} - p_{th}^{j,k}}{p_{rate}^{j,k}} \quad (1)
$$

请注意，我们假设采用非线性能耗模型。是否应使用具有最大使用时间tj,k的VF fj中的车辆 k来分担来自MEC系统ei的卸载工作负载，取决于具体应用。某些应用仅需处理短无状态事务，此时较小的tj,k已足够。然而，其他一些应用可能需要较大的tj,k，以避免与有状态工作负载迁移相关的开销。设 Di为来自 ei的工作负载所要求的最小服务时间D。我们用 Vj表示在VF fj中几乎可以确定可用且满足tj,k ≥ Di的车辆集合。只有 Vj中的车辆才可被考虑用于处理卸载的请求，以维持一定水平的服务质量。

当多个MEC系统将请求卸载到一个共同的VF时，来自同一MEC的所有请求由独占分配的车辆集合共同处理。设vik,j为指示车辆 k ∈ Vj被分配以服务从 ei卸载的工作负载的变量。定义 V i j={k ∈ Vj | vik,j= 1}。对于任意两个MEC系统 ei和 ei′，我们有⋃i V i j ∩ V i′ j= ∅。

类似于MEC系统，VF中的每辆车也被建模为具有统一服务速率 μv的M/M/1队列。因此，分配给同一MEC系统以处理卸载请求的同一VF中的 c车辆组可被建模为 M/M/c队列。

不同的卸载配置会产生不同的分配成本。我们假设同一MEC系统中的所有MEC服务器 ei具有相同的计算成本 ci。因此，当激活ˆmi个MEC服务器中的 mi个时， ei的总计算成本为 mici。另一方面，我们假设车辆具有异构的分配成本。我们使用 ck j 表示分配车辆 k ∈ Vj的成本。设λi j 为从 ei卸载到 fj的请求速率。 ei本地处理的请求的平均速率为
$$
\lambda_e^i = \lambda_{in}^i - \sum_{j=1}^{|F|} \lambda_i^j \quad (2)
$$

在稳态下， λe i应小于 miμi，其中 mi表示在 ei中分配的 MEC服务器数量。当满足该条件时，由 ei服务的请求的计算时延是定义为 mi的函数
$$
l_e^i(m_i) = \frac{C(m_i, \lambda_e^i / \mu_i)}{m_i \mu_i - \lambda_e^i} + \frac{1}{\mu_i} \quad (3)
$$
其中，C(c, λ/μ) 是厄兰C公式 [31]，定义为
$$
C(c, \lambda/\mu) = \frac{1}{1+(1 - \rho)( c! / (c\rho)^c) \sum_{k=0}^{c-1} (c\rho)^k / k!} \quad (4)
$$
其中 λ是到达流量速率， μ是服务速率， ρ=λ/(cμ)。

设n i j = |V i j | 为 V i j 中的车辆数量，l f j ,i(n i j )为这些n i j 车辆相关的计算时延。与移动边缘计算情况类似，我们有
$$
l_f^{j,i}(n_{ij}) = \frac{C(n_{ij}, \lambda_i^j / \mu_v)}{n_{ij} \cdot \mu_v - \lambda_i^j} + \frac{1}{\mu_v} \quad (5)
$$

符号	定义
E	MEC系统集合
F	虚拟功能集合
λin i	进入MEC系统ei的用户请求到达率
Lmax i	用户请求的延迟约束
Di	工作负载的最小服务时间
mi	分配给MEC系统ei的服务器数量
vik,j	指示车辆k是否被分配给MEC系统ei的变量
λi j	从MEC系统ei卸载到虚拟功能fj的请求速率

表II 关键符号汇总

我们假设每个MEC系统都有一个到每个VF系统的专用信道。每个信道中的通信延迟由排队延迟、传输时间和传播延迟组成。排队延迟加上传输时间被建模为一个M/M/1队列，其均值服务速率为 μef。传播延迟等于di,j（ ei与 fj之间的距离）除以信号速度 s。形式上，
$$
l_{ef}^{i,j} = \frac{1}{\mu_{ef} - \lambda_i^j} + \frac{d_{i,j}}{s} \quad (6)
$$
其中λ i j < μef。这意味着卸载的流量不能超过信道容量。

在处理来自 ei的请求后， fj 需要将结果发送回 ei。回程流量应为请求流量的一部分。设 ε i为从fj 到 ei的回程流量速率与 λ i j 之比。设 μfe为从虚拟功能到移动边缘计算的信道的平均服务速率。回程流量的通信延迟l fe j ,i可估计为
$$
l_{fe}^{j,i} = \frac{1}{\mu_{fe} - \lambda_i^j \cdot \varepsilon_i} + \frac{d_{i,j}}{s} \quad (7)
$$
与λ i j · εi < μ fe。

表II 总结了我们问题表述中将使用的关键符号。

III. 问题建模

卸载配置旨在决定每个MEC系统中已分配的MEC服务器数量、每个MEC系统中每个虚拟功能（VF）对应的已分配车辆集合，以及从MEC系统到每个VF的卸载比率，以在满足每个用户请求的端到端延迟约束的同时最小化总成本。形式上，卸载配置的目标是
$$
\min_{{m_i} i,{v {k}^{i,j}} {k}^{i,j},{\lambda_i^j} {ij}} \sum_{i=1}^{|E|} \left( m_i c_i + \sum_{k \in V_j} v_{k}^{i,j} c_k^j \right) \quad (8)
$$
目标受限于以下约束条件。
$$
\lambda_{in}^i - \sum_{j=1}^{|F|} \lambda_i^j < m_i \cdot \mu_i, \forall i \quad (9)
$$
$$
\lambda_i^j < |V_i^j| \mu_v, \forall i, j \quad (10)
$$
$$
0 \le m_i \le \hat{m} i, \forall i \quad (11)
$$
$$
0 \le \sum {i=1}^{|E|} \sum_{k \in V_j} v_{k}^{i,j} \le |V_j|, \forall j \quad (12)
$$
$$
l_e^i(m_i) \le L_{max}^i, \forall i, m_i > 0 \quad (13)
$$
$$
l_e^i,f_j + l_f^{j,i}(|V_i^j|) + l_{fe}^{j,i} \le L_{max}^i, \forall i, j, \lambda_i^j > 0 \quad (14)
$$
$$
v_{k}^{i,j} = 1 \rightarrow t_{j,k} \ge D_i, \forall i, j, k \quad (15)
$$
$$
v_{k}^{i,j} \in {0, 1}, \forall i, j, k \quad (16)
$$
公式(9)和(10)确保：针对ei的请求，若由 ei本地服务或被卸载至 fj，其到达率应分别低于分配给 ei和 fj的服务速率。公式(11)表示分配的服务器数量不得超过 ei中可用服务器的数量。公式(12)确保分配用于服务卸载请求的 fj中的车辆总数不超过可分配车辆的数量。公式(13)指出，当请求 ei由 mi个MEC服务器本地服务时，其延迟( le i( mi))不应超过相应的延迟约束 Lmax i 。对于相同请求被卸载并由VF fj 处理的情况，总延迟（包括通信和计算延迟）也不应超过 Lmax i ，如(14)所示。公式(15)要求只有使用时间不小于最小服务时长的车辆才可被分配。公式(16)限制vk i, j为指示变量。

上述定义的成本最小化问题是一个混合整数规划问题，可证明为NP难[32]。因此，求解该问题的最优解计算代价高。此外，多接入边缘计算系统并不受单一个人或机构控制。事实上，我们假设存在独立MEC服务提供商，他们仅基于自身商业利益做出决策。因此，由于MEC服务提供商可能缺乏遵循最优结果的动机，全局最优解几乎无法实现。为此，我们提出一种面向独立MEC系统的去中心化方法。

IV. 去中心化卸载配置协议（DOCP）

本节介绍了每个MEC系统ei用于确定其卸载配置并向相应VF管理器请求车辆的去中心化卸载配置协议（ DOCP）。对于每个独立的MEC系统 ei，其局部目标是
$$
\min_{m_i,{\lambda_i^k}} c_i^{total} = m_i \cdot c_i + \sum_{k \in V_j} v_{k}^{i,j} c_k^j \quad (17)
$$
受相同的约束条件(9)至(16)限制。DOCP 还作为下一节中提出的冲突解决协议的基础。

A. 协议

DOCP 的总体行为如下：在 MEC 系统确定其卸载配置之前，会查询每个联邦虚拟车队的工作负载处理能力 以及 相关成本。在 MEC 系统确定其 卸载配置 后，它会向相应的 VF管理器 请求一定数量的 车辆。如果管理器批准该请求，则会将来自 MEC 的后续 流量 调度 至分配给该 MEC 的 车辆 集合。

当具有延迟约束 Lmax i和最小服务时间 Di的工作负载 λin 到达MEC ei时，算法1中提出的EVF贪婪方法尝试将 λin i分配给MEC ei和/或多个VF，以最小化总成本。该算法首先重置解集 S，并将候选集 U初始化为包含MEC ei和所有VF。待分配的处理负载Λ初始设置为 λin i。对于尚未被加入 S的每个元素 j ∈ U，算法计算其服务能力 λ j和相关成本 cj，这通过调用edge_alloci(Λ, Lmax i)或vfog_allocj(Λ, Lmax i, Di)实现，具体取决于 j是ei还是一个VF。在 U中的所有候选者中，算法选择单位成本下服务能力最高的 u ∈ U，将其加入 S，并从Λ中减去其容量 λu。只要Λ和 U均不为空，该选择过程就重复进行。选择过程完成后，算法将结果与零卸载方案进行比较，即对所有 j采用 λ i j = 0。如果零卸载可行且总成本更低，则选择零卸载方案。

设 λ e i = λ in i −∑j λ i j 为 ei本地处理的请求速率。如果对于某个满足 λ e i = λ in i 的mi ≤ ˆmi， l e i( m i) ≤ L max i 成立，则零卸载是可行的。由于MEC被建模为M/M/c队列，给定 λ e i 和 m i 后，我们可以很容易地计算出 l e i( m i)。图3展示了M/M/c中延迟（平均等待时间）与服务器数量之间的关系。给定工作负载 λ和延迟约束 L max后，算法2尝试在 e i 中分配最少数量的服务器以实现零卸载，并计算相关成本。如果零卸载不可行，算法2将通过二分法[33]（如算法3所示）确定 e i 在仍满足延迟约束的前提下所能处理的最大工作负载（请求到达率）。

算法4 详细描述了在虚拟功能 fj 中为处理具有延迟约束 L max 和服务持续时间 D 的工作负载 λ 所进行的车辆分配。车辆分配比

授权许可使用仅限于：卡尔顿大学。下载时间：2021年5月28日 23:24:54 UTC，来源：IEEE Xplore。适用限制。
授权许可使用仅限于：卡尔顿大学。下载时间：2021年5月28日 23:24:54 UTC，来源：IEEE Xplore。适用限制。

由于虚拟功能中存在异构车辆成本和使用时间， ei中的边缘服务器分配需要确定是否分配每个单独的车辆 k ∈ V j ，其分配成本为c k j ，使用时间为t j ,k，以满足相应的延迟约束 L max，同时最小化车辆分配成本。我们通过一种启发式方法构建 V i j ，该方法同时考虑了车辆的成本和使用时间。初始时，V i j 被设为空。所有在 V j 中使用时间不小于 D的车辆均有资格参与分配。该算法按照车辆使用时间 与成本比(U/C)或仅按使用时间的非递减顺序逐一进行合格车辆的分配。当满足以下条件时，分配停止

参数	MEC系统ei	VF f1	VF f2
ˆmi / μi / ci	5 / 200 / 200	-	-
aj / dj / μv	-	2 / 1 / 5	3 / 1 / 5
车辆k	-	1, 2	1, 2, 3
pres j,k / prate j,k / ck j	-	100/10/15, 100/10/15	100/10/25, 100/10/25, 100/10/25

表III 运行示例的系统参数

轮次	候选者	λj	cj	λj/cj	选择	Λ
(a) λin i = 20 rps
1	ei	20	200	0.10	f1	20
	f1	8.9	30	0.297
	f2	13.9	75	0.185
2	ei	11.1	200	0.056	f2	11.1
	f2	11.1	75	0.148
(b) λin i = 205 rps
1	ei	199	200	0.995	ei	205
	f1	8.9	30	0.297
	f2	13.9	75	0.185
2	f1	6	30	0.200	f2	6
	f2	6	25	0.240

表IV 算法执行

当与 V i j 相关的延迟已经小于 Lmax，或无法再分配更多车辆时。在后一种情况下，意味着 V i j 中的车辆无法处理 λ 以满足延迟约束，我们计算 V i j 中的车辆 collectively 能够处理的最大工作负载λmax，且其延迟等于或小于 Lmax。该值也可通过二分法求得。

算法3的时间复杂度为 O(log(λ))。相应地，算法2和算法4的时间复杂度分别为 O(mi+log(λ in i))和 O(|Vj|log(|Vj|) + log(λ in i))。算法1中的主循环最多包含 |F| 次迭代。循环中的第5行最多执行一次。对于第8行，每次迭代的时间复杂度为 O(|F|Vmax log(Vmax) +|F| log(λ in i))，其中 Vmax= max j |Vj |。因此，算法1的时间复杂度为 O( |F|2( |F| log(Vmax) +log(λ in i)) + mi)。

B. 运行示例

我们给出一个DOCP的简单运行示例如下。我们假设一个MEC系统 e i 和两个虚拟功能 f1 和 f2 ，其系统参数如表III所示。假设每秒有 λ in i = 20个请求（rps）和 L max i = 1秒。由于 l e i (ˆmi) = 1/(μ i − λ in i )= 0.0056不超过L max i ，零卸载是可行的，成本为 c i = 200。对于VF

授权许可使用仅限于：卡尔顿大学。下载时间：2021年5月28日 23:24:54 UTC，来源：IEEE Xplore。适用限制条款。

f1，由于 V1中的所有车辆的使用时间均大于 L max i ，因此可以利用其聚合服务速率 2μv= 10rps。在此服务速率下，若由 f1 单独处理 λ in i ，总延迟为 L′> L max i 。因此算法4计算 λ max = max_capacity1(20, 1, 2) = 8.9，即在延迟不超过 L max i 的前提下所能处理的最大工作负载f1。与此分配相关的成本为 ∑k c k 1 = 30。类似地， λ max = 13.9的成本为75，用于 f2。随后算法1从 e i 、 f1和f2中选择具有最高成本容量比的系统。如表IV(a)所示， f1 将首先被选中以处理λ in i 的一部分，剩余工作负载 λ= 20 −8.9= 11.1交由 e i 和 f2 处理。在第二轮中，由于 f2 具有更高的成本容量比，将被选中

比例。 f2中所有车辆的分配使得没有剩余工作负载需要处理。总成本为105。

如果我们将 λin i增加到205 rps， ei的成本容量比将高于 f1和 f2。因此，在第一轮中将选择容量为199 rps（经过取整后）的 ei（表IV(b)），剩余6 rps的工作负载待处理。注意，在第一轮中 f1的成本容量比高于 f2。然而，在第二轮中 f1相对于 f2的优势不再成立，因为两个虚拟功能都分配了两辆车来处理剩余工作负载，但与 f1相关的成本高于 f2。

V. 多MEC系统的匹配协议

接下来，我们提出一种基于请求‐响应范式的多MEC多 VF EVF架构的匹配协议。在该协议的一般框架中，每个 MEC系统独立选择一组虚拟功能以提交其卸载请求。由于一个虚拟功能可能同时收到来自多个MEC系统的卸载请求，因此它会临时批准其中一部分请求，而拒绝其余请求，且不与其他虚拟功能进行协调。对于被拒绝请求的MEC系统，可随后向其他虚拟功能重新提交请求。另一方面，一个虚拟功能只要能够通过拒绝获得更优结果，就可以后续拒绝之前已临时批准的请求。当所有MEC系统均无剩余请求需要提交时，协商过程结束。

在匹配理论的背景下，MEC系统集合E和虚拟功能集合 F是两组代理。匹配关系将MEC系统 ei映射到虚拟功能 ej，反之亦然，如果λi j > 0。该匹配关系是多对多[34]，因为一个MEC系统可以将其工作负载卸载到多个虚拟功能，而一个虚拟功能可以服务于来自多个MEC系统的卸载请求。

在所提出的方法中，每个 ei ∈ E根据定义在所有可能的虚拟功能集合上的偏好关系 e i 来决定提交请求的虚拟功能集合。对于任意两个虚拟功能集合 S, T ⊆ F，关系 S e i T 表示 ei比 T更偏好 S。同样，每个fj ∈ F根据定义在所有可能的MEC系统集合上的偏好关系f j 来决定授予的请求集合。对于任意两个MEC系统集合 S, T ⊆ E，关系 S f j T意味着fj 比 T更偏好 S。对于每个 ei ∈ E和 F′ ⊆ F,，我们定义C(F,′ e i) 为根据 ei的偏好关系 e i ， ei对 F′的最优先子集。类似地，对于每个 fj ∈ F和E′ ⊆ E,，我们定义 C(E,′ f j )为根据 fj 的偏好关系 f j ， fj 对 E′的最优先子集。

A. 协议

匹配协议按轮次进行。在每一轮中，每个MEC系统 e i 独立使用算法1来获得一个卸载配置，该配置指定了从每个虚拟功能 fj ∈ S请求的可能车辆集合(V i j ⊆ V)。如果 e i自身也处理用户的工作负载（即 e i ∈ S），则首先计算其容量λ e i ，并从总工作负载Λ中扣除。如果卸载配置中存在任何虚拟功能，则 e i 随后从 S中选择最优先的虚拟功能子集（即 C(S{ei} ,e i )）提交其资源请求。如果向某个 f j 发出的请求被接受，则计算要卸载到 f j , λ i j 的工作负载量，并从 Λ中减去。否则，如果 e i 收到一个

授权许可使用仅限于：卡尔顿大学。下载时间：2021年5月28日 23:24:54 UTC，来源：IEEE Xplore。适用限制条款。

算法5：每个 ei ∈ E 的过程。
1: Λ ← λin i
2: Ai ← ∅ 接受 ei请求的虚拟功能集合
3: (S, V, ctiotal) ←EVF_alloci(F,Λ, Lmax i, Di)
4:如果 ei ∈ S那么
5: (λe i, c e i)
6: Λ ←Λ − λe i
7:结束 if
8:当 V= ∅时执行 do
9: Pi ← C(S{ei},ei)
10:向每个 fj ∈ Pi 发送 req(|V i j |, mvi,j)
11:对于所有 决策从每个 fj执行 do
12:如果决策= ACCEPT则
13: Ai ← Ai ∪{fj}
14: λi j ← max_容量j(Λ, Lmax i, |V i j |)
15: Λ ←Λ − λi j
16:否则如果 decision=拒绝 且 fj ∈ Ai那么
17: Ai ← Ai{fj}
18: Λ ←Λ+ λi j
19：结束如果
20:结束循环
21: F ← F\ Pi
22: (S, V, ci total) ←EVF_alloci(F,Λ, Lmax i, Di)
23:结束循环

对应于先前已接受请求的拒绝，该请求对应的工作负载将重新加回到 Λ。此过程重复进行，直到不再需要或无法进行卸载请求为止。每个 ei的详细过程如算法5所示。

该过程的一个潜在问题是，结果可能对MEC系统而言不是个体理性的。也就是说，在此结果下，某些MEC系统通过取消与某些VF的匹配可以获得更好的收益。例如，假设 ei向 C(S{ei},e i) 中的每个VF发送一个请求，但只有 f2和f3接受 ei的请求。如果{f2, f3} ⊆ C(S{ei, f1},e i) ，那么当排除 f1的考虑时，ei可能会进一步向 C(S{ei, f1},e i) 中的所有VF发送请求以获得最理想的结果。然而，如果{f2, f3} ⊆ C(S{ei, f1},e i) ，则当VF f2或 f3（或两者，取决于该VF是否在 C(S{ei , f1},e i )中）拒绝其请求时， ei会更加满意。这种情况的发生是因为车辆具有异质性的分配成本。

为确保个体理性，我们定义 C(F,e i )为e i在 F（单元素 集合）中最偏好的虚拟功能。形式上，
$$
C(F,e_i) = {f_j \in F | {f_j} e_i {f’ j}, \forall f’_j \in F}, \quad (18)
$$
其中 {fj} e i {f′ j } 如果 fj = f′ j 或 {fj} e i {f′ j }。
对于MEC系统对虚拟功能集合的偏好，我们定义MEC ei对每个虚拟功能 f j ∈ F的偏好值为 P i(fj ) = |V i j |，即从 f j 分配的车辆数量。相应地，我们对每个 F ′ ⊆ F有如下定义：
$$
C(F’, e_i) = {f_j \in F’ | |V_i^j| \ge |V_i^{j’}|, \forall f {j’} \in F’}. \quad (19)
$$
我们在附录中证明了所有匹配结果对于所有MEC系统都是个体理性的另。另一方面，虚拟功能（VF）只要拥有充足的资源，就会批准所有收到的卸载请求。如果虚拟功能（VF）的资源不足以满足所有卸载请求，则会选择性地批准部分请求，同时拒绝其他请求。此处选择规则的关键在于尽可能最小化总成本。在所提出的方法中，虚拟功能（VF） fj的选择基于当 fj服务 ei时，每个 ei的总成本的减少量。令 ci total( F)表示当 ei以及 F中的所有虚拟功能（VFs）参与卸载配置时，由EVF_alloci(F, λin i, Lmax i, Di)（参见算法1）返回 的 ei的总成本。候选元素u fj相对于 ei的边际价值为
$$
mv_{i,j} = c_i^{total}(F\backslash{f_j}) - c_i^{total}(F). \quad (20)
$$
边际价值的概念基于社会福利最大化[35]。注意，fj相对于 ei的边际价值由 ei计算并告知。

虚拟功能在轮次中接收请求。设 E(k)为在第 k ≥ 1轮中向虚拟功能 fj发送请求的移动边缘计算系统集合。设 A(k) j 为在某一轮 k′< k中请求已被接受，且在第 k轮开始时尚未被 fj拒绝的所有移动边缘计算系统的集合。fj在第 k轮中考虑的移动边缘计算系统集合为 A(k) j ∪E(k)。理论上， fj应从该集合 E′中选择一个子集以批准请求，从而最大化 ∑ei∈E ′ mi,j（受限于 fj的资源约束）。形式上，给定一组移动边缘计算系统 E，令Ωj(E)表示 E的所有子集组成的集合，其总需求不超过 fj的供应量。根据(20)。
$$
C(E,f_j) = \arg \max_{E’ \in \Omega_j(E)} \sum_{e_i \in E’} mv_{i,j} \quad (21)
$$
不难看出，求解 C(E,fj) 正是0/1背包问题，这是一个 NP完全问题。我们采用贪心方法，按照请求的边际价值非递增的顺序逐个处理MEC系统的请求。在确定P j = C( A(k) j ∪E(k),f j )后，对于MEC系统在 P j\A(k) j 中的任何请求都应接受，而对于在 E(k)\Pj和 A(k) j \ Pj中的MEC系统的请求则应拒绝。详见算法6。

算法5的主循环最多执行|F| 次，其中第9行耗时 O( |F|)，第14行耗时O(log(λ in i))。因此，算法5的时间复杂度为 O(|F|3(Vmax log(Vmax) +log(λ in i)) + |F|mi)。对于算法 6，最大轮数为 |F|。在每一轮中，第5行耗时 O(|E|log( |E|))。因此，算法6的时间复杂度为 O(|F||E| log(|E|))。

B. 运行示例

我们使用两个示例来说明所提出的匹配协议的执行过程。我们假设有两个MEC系统和三个VF，其设置如表V所示。

参数	MEC e1	MEC e2	VF f1	VF f2	VF f3
ˆmi / μi / ci	5 / 200 / 200	5 / 200 / 200	-	-	-
aj / dj / μv	-	-	2 / 1 / 5	2 / 1 / 5	2 / 1 / 5
车辆k	-	-	1, 2	1, 2	1, 2
pres j,k / prate j,k / ck j	-	-	100/10/15, 100/10/15	100/10/15, 100/10/15	100/10/15, 100/10/15

表V 参数（案例1）

轮次	e1	e2	f1	f2	f3
1	请求f1	请求f3	接受e1	-	接受e2
2	请求f3	请求f3	-	-	拒绝e1, 接受e2
3	请求f2	-	-	接受e1	-

表VI 匹配协议执行过程（案例1）

它们之间存在冲突。第一轮结束后， e1和 e2均仍有剩余工作负载。在第二轮中，它们都争夺 f3中的车辆资源。由于 f3仅剩两辆车，无法同时满足两个请求。因为mv2,3 > mv1,3, f3接受e2的请求并拒绝 e1的请求。在第三轮中， e1是唯一一个因资源充足而被接受请求的请求者。请注意，在最后一轮中 mv1,2值较高。原因是如果没有 f2提供的资源， e1将不得不启动自身昂贵的服务器来处理剩余的工作负载。

我们使用第二个示例来展示虚拟功能对总成本的影响。除了 λ in i 和 μ v（表VII）之外，我们使用与前一个示例相同的设置。在第一轮中， e 1和 e 2都向 f1发送请求，而 f1需要拒绝其中一个请求，因为 f1 没有足够的车辆。如果 f1 的决策基于所提出的方法中的边际价值，它将接受e 1 的请求，同时拒绝 e 2 的请求，如表VIII所示。

参数	MEC e1	MEC e2	VF f1	VF f2	VF f3
ˆmi / μi / ci	5 / 200 / 200	5 / 200 / 200	-	-	-
λin i	100	100	-	-	-
aj / dj / μv	-	-	2 / 1 / 5	2 / 1 / 5	2 / 1 / 5
车辆k	-	-	1, 2	1, 2	1, 2
pres j,k / prate j,k / ck j	-	-	100/10/15, 100/10/15	100/10/25, 100/10/25	100/10/25, 100/10/25

表VII 参数（案例 2）

轮次	e1	e2	f1	f2	f3
1	请求f1	请求f1	接受e1, 拒绝e2	-	-
2	请求f2	请求f3	-	接受e1	接受e2
3	-	-	-	-	-

表VIII 匹配协议执行过程（案例2）

轮次	e1	e2	f1	f2	f3
1	请求f1	请求f1	拒绝e1, 接受e2	-	-
2	请求f2	-	-	接受e1	-
3	-	-	-	-	-

表IX 采用替代偏好的匹配协议执行过程（案例2）

参数	范围
(a) 单MEC系统
ˆmi	5
μi	200 rps
ci	$200
|F|	10
aj	[0, 20]
dj	[0, 20]
μv	5 rps
pres j,k / prate j,k / ck j	100%/10%/[0, 20]$
λin i	[0, 2000] rps
Lmax i	1 sec
Di	1 sec
(b) 多MEC系统
|E|	5
|F|	20
ˆmi	1, 2, or 4
μi	[100, 500] rps
ci	$1000
aj	[0, 20]
dj	[0, 20]
μv	5 rps
pres j,k / prate j,k / ck j	100%/10%/[0, 20]$
λin i	Normal(μ=[0,1000], σ=μ/4)
Lmax i	1 sec
Di	1 sec

表X 仿真参数

总成本为32美元，分配了三辆车。或者，如果决策基于请求的车辆数量，则 f1将拒绝 e1的请求，但接受 e2的请求， 如表IX所示。此时总成本变为36美元，分配了四辆车。在此示例中，以边际价值作为优先考虑优于另一种方案。

VI. 数值结果

我们进行了仿真以评估DOCP和所提出的匹配协议的性能。所有的仿真程序均使用Python编写。我们假设一个半径100公里的盘状覆盖区域，MEC系统和VF在此区域内随机分布。每个结果均为50次试验的平均值。

A. DOCP的性能

我们首先考虑了一个由一个MEC系统和10个VF组成的电动汽车群系统。其他参数列于表Xa中。

我们改变了平均用户流量速率 λ in i ，以研究其与总成本的关系。图4a显示了所提出的方法的结果。

授权许可使用仅限于：Carleton University。于2021年5月28日从IEEE Xplore下载，下载时间：23:24:54 UTC。适用限制。

ˆmi= 5, µi= 200 rps， ci=$200。(b) ˆmi= 1, µi= 1000 rps， ci=$100 0.)

λin = 100 rps。(b) λin = 1500 rps。)

我们观察到，当用户流量速率较低（例如 λin i< 500 rps）时，所提出的方法更倾向于将用户流量卸载到虚拟功能（VF），而不是由MEC服务器进行本地计算。原因是当用户流量远超单个 MEC服务器的容量时，将全部工作负载卸载到虚拟功能（VF） 是一种更具成本效益的解决方案。随着用户流量速率的增加，利用MEC服务器承担部分工作负载相比将全部工作负载卸载到虚拟功能（VF）更具成本效益。因此，DOCP找到的卸载配置是本地计算和卸载的混合方案。当用户流量速率增加到一定程度时，必须激活所有MEC服务器以首先处理用户流量，然后由虚拟功能（VF）处理所有剩余的工作负载。因此，当 λ in i >1000 rps时， 总成本仅因虚拟功能（VF）的贡献而增加。

我们采用了另一种设置以更清晰地观察该场景。我们使用了相同的配置，但将e i中的五个服务器替换为一个大型服务器。该大型服务器的服务速率和成本均为原始服务器的五倍。如图4 b所示，当 λ in i < 500或 λ in i > 1000 rps时，结果与之前相同。当 λ in i 设置为中间某个值时，总成本来自MEC服务器和VFs的混合使用。然而，总成本略高于之前的设置，这是因为之前的设置比此设置提供了更细粒度的计算资源。

接下来，我们改变了延迟约束 L max i 并测量了总成本。图5 a显示了在 λ in i = 100 rps下的结果。满足严格的延迟约束所需的资源量较大，因此，MEC服务器比车辆更具成本效益。当我们放宽延迟约束至 Lmax i> 0.2秒时，转而利用虚拟功能，因为此时车辆比MEC服务器更具成本效益。这样做可将总成本从200美元降低到约40美元。

图5 b展示了在高用户流量（λin i = 1500rps）下的结果。在此工作负载下，仅靠MEC服务器无法在满足延迟约束的同时处理所有用户流量，因此始终需要额外的车辆进行卸载。特别是当 Lmax i < 0.3 sec时，所有车辆都被使用。然而，随着延迟约束的放宽，用于卸载的车辆数量显著减少。这解释了总成本曲线急剧下降的原因。

B. 匹配协议的性能

我们考虑了一个包含五个多接入边缘计算系统和20个虚拟功能的场景。除了表Xb中列出的参数外，我们还假设每个虚拟功能 fj 的车辆到达率为 a j ，离开率为 d j 。 a j 和 d j 的值在范围[0,20]内随机确定。每辆车的服务速率为5 rps。同一MEC系统中的所有MEC服务器具有相同的服务速率，而不同MEC系统中的服务率则随机确定。

我们使用正态分布来设置每个 e i ∈ E的用户流量速率 λ in i 。我们将该分布的均值从0变化到1000 rps，标准差设为均值的四分之一

授权许可使用仅限于：Carleton University。于2021年5月28日23:24:54 UTC从IEEE Xplore下载。限制适用。

λin i= 0至200 rps。(b) λin i= 0至1000 rps.)

均值。图6 a展示了使用所提出的匹配协议的结果。合理的是，总成本随着用户流量的增加而增加。当 λin i的均值不超过40 rps时，所有工作负载仅由虚拟功能处理。当 λin i的均值大于40 rps时，引入MEC服务器以分担工作负载，从而最小化总成本。随着工作负载增加到某种程度，仅靠 MEC服务器无法处理全部用户流量，因此未满足的工作负载被卸载到虚拟功能。从该点开始，总成本与虚拟功能的成本成正比（图6b）。

我们还使用指数分布来生成用户流量，但未观察到显著差异。

接下来，我们研究了MEC服务速率的粒度是否会影响总成本。为此，我们通过改变每个MEC系统中的服务器数量，并将MEC系统的总服务速率平均分配给每个服务器来实现。图7展示了当每个MEC系统分别具有1、2或4个 MEC服务器时，总成本随用户流量速率增加的变化情况。结果表明，更细粒度的MEC服务速率通常会导致更低的总成本，这与我们在单个MEC系统中的结果一致。

我们研究了车辆成本对卸载比率以及总成本的影响。每辆车的成本从0美元变化到20美元。如图8所示，当每辆车的成本不超过4美元时，仅使用车辆，因此总成本仅由虚拟功能产生。当车辆成本高于4美元时，MEC服务器比车辆更具成本效益，因此优先使用MEC服务器。当所有 MEC服务器都被使用后仍需要虚拟功能进行卸载时，总成本随着车辆成本的增加而上升。

C. 与其他方法的比较

作为对比，我们考虑了三种替代方案来对比所提出的匹配算法。前两种方案，NumFirst和CostFirst，均为贪心且集中式的启发式方法。它们首先使用算法1确定每个MEC系统需要卸载的用户流量数量，然后以贪心方式将MEC系统与 VF进行匹配。这两种方法均选择剩余工作负载最多的MEC系统。对于该MEC系统与VF的匹配，NumFirst选择车辆数量最多的VF，而CostFirst选择成本最低的VF。此匹配过程重复进行，直到没有MEC系统存在可卸载的剩余工作负载为止。

第三种选择是粒子群优化（PSO）算法。作为一种元启发式方法，粒子群优化（PSO）最初在[36]中被提出，已被广泛应用于解决许多应用领域中复杂且困难的优化问题。PSO将优化问题的潜在解表示为一个粒子群或类似生物体的群体，其移动方式类似于鸟群。该算法通过在搜索空间中移动粒子来迭代地改进现有解，每个粒子的新位置由其自身的局部最优位置、移动速度以及所有粒子的全局最优位置共同决定。这一寻解过程本质上模拟了鸟类的 flocking 行为。一般来说，PSO所产生的解的质量取决于允许粒子移动的最大迭代次数。

我们首先固定车辆成本，并将所提出的匹配协议与 NumFirst和CostFirst进行比较。图9显示了结果。当用户流量速率较低时，所提出的方法优于NumFirst和CostFirst。性能

授权许可使用仅限于：卡尔顿大学。下载时间：2021年5月28日 23:24:54 UTC，来源：IEEE Xplore。适用限制条款。

λin i ∈[0200]. (b) λin i ∈[0600].)

λin ∈[0200]。(b) λin ∈[0600]。)

λ in i ∈[0200].(b) λ in i ∈[0600]。)

NumFirst 在用户流量速率较低时与 CostFirst 相似，但在用户流量速率较高时优于 CostFirst。CostFirst 表现不佳是因为在此设置中车辆成本是同质的。

接下来，我们在表Xb中指定的车辆成本随机确定的情况下进行了实验。结果如图10所示。所提出的方法在所有用户流量速率设置下再次表现出最低的成本。在高用户流量速率下，我们方法的优势尤为显著（成本降低约40%）。在此情况下，CostFirst的表现优于NumFirst，这可以通过本实验中车辆成本具有异质性来解释。

图11比较了所提出的匹配方法与粒子群优化（PSO）在两种不同最大迭代次数设置下的成本（maxiter）。所提出的匹配方法比使用maxiter= 50的粒子群优化（PSO）表现好得多，且略逊于使用maxiter= 500的粒子群优化（PSO），这并不令人意外。尽管如此，我们强调，粒子群优化（PSO）是一种集中式离线方法，不适合作为在动态环境中执行的协议使用。所提出的匹配方法本质上是分布式的，可作为在所提出的EVF环境中实际可行的解决方案。

VII. 结论

我们提出了一种双层EVF架构，用于实现从多接入边缘计算系统到虚拟功能的计算卸载。该最优卸载问题以最小化总成本为目标，已被建模为一个混合整数规划问题。作为

授权许可使用仅限于：卡尔顿大学。2021年5月28日从IEEE Xplore UTC时间23:24:54下载。适用限制。