
论文链接:https://www.aaai.org/ojs/index.php/AAAI/article/view/4471/4349
代码链接:https://github.com/ydzhang-stormstout/HHNE
会议:AAAI 2019
文章目录
1 摘要
复杂网络的结构可能有着双曲的几何特征,因为双曲结构可以天然地反映出复杂网络的一些属性,比如hierarchical(层级)结构和power-law(幂律)结构。本文是第一个在双曲空间中研究HIN嵌入问题的。
文章分析了两个真实的HIN,并发现了其存在power-law distribution等属性,因此提出了双曲的异质信息网络嵌入模型。
文章使用了meta-path指导的随机游走采样得到训练数据,利用了节点在双曲空间中的距离作为相似度度量。双曲距离符合三角不等式,且可以很好地保留HIN中的传递信息。作者还进一步推导出迭代更新双曲嵌入的有效优化策略。
在网络重构(network reconstruction)和链接预测(link prediction)任务中表现出了优于state-of-the-art的效果。通过可视化,也表现出了捕获HIN层级结构的能力。
2 介绍
关注的根本问题为HIN的嵌入学习问题。
2.1 现有的方法
现有的方法大致可以分为:基于随机游走的方法;基于网络分割的方法;基于深度神经网络的方法。
这些方法都聚焦于如何有效地捕获HIN的结构和语义信息,然而还有一个基本的问题:HIN的适合的或内在的等轴空间(isometric spaces)是什么?
也有一些研究将网络嵌入到低维的双曲空间中,但是它们都只是对同质网络的节点进行表示学习,没有考虑异质的复杂信息网络。
HIN嵌入方法有Metapath2vec(Dong, Chawla, and Swami 2017)、HIN2vec(Fu, Lee, and Lei 2017)、PTE(Tang, Qu, and Mei 2015)、EOE(Xu et al. 2017)、HNE(Chang et al. 2015)、SHINE(Wang et al. 2018)。这些方法都是将HIN建模在了低维的欧式空间中,然而欧式空间是否是最合适的选择还有待研究。
2.2 动机
欧式空间已成为当前HIN嵌入方法的主流选择,但是越来越多的研究表明,许多复杂的数据(如:社交网络),有着高度非欧几里得的潜在信息。
这引发了作者的思考:1)现有的HIN嵌入模型常用的低维空间(欧式空间)是否是合适的?2)是否有其他可行的非欧空间?
2.3 双曲空间
双曲空间是常负曲率空间,它比欧式空间扩张速度快(文章中有举例),所以更易于对有着低维嵌入表示的复杂数据建模。
Krioukov(2010)等人将双曲空间作为复杂网络的基础,并且发现了有幂律(power-law)结构的数据适合于在双曲空间中建模。Dhingra(2018)等人将文本表示在了双曲空间中,(Nickel and Kiela 2017)和 (Ganea, Becigneul, and Hofmann 2018) 在双曲空间中学习到了同质网络的嵌入表示。
2.4 作者提出
作者提出HHNE模型(hyperbolic heterogeneous information network embedding ),在双曲空间中获得网络的结构和语义信息。
使用元路径指导的随机游走,获取HIN中的结构信息和语义关联信息。
节点在双曲空间中的距离,作为节点间相似度的衡量标准,距离符合三角不等式,且可以很好地保留HIN中的传递信息。
模型实现了最大化邻域节点间的相似度,最小化负采样节点间的相似度。作者还进一步推导出迭代更新双曲嵌入的有效优化策略。
2.5 贡献
(1)第一个在双曲空间进行HIN的嵌入学习;
(2)提出HHNE模型,解决上述问题;
(3)进行实验验证了HHNE的表示能力,效果优于state-of-the-art。
3 Embedding HIN in Hyperbolic Spaces
3.1 问题定义
(1)HIN(异质信息网络)
定义图为 G = ( V , E , T , ϕ , ψ ) G=(V,E,T,\phi,\psi) G=(V,E,T,ϕ,ψ), V V V和 E E E分别是节点集合和边集合。 ϕ ( v ) : V → T V , ψ ( e ) : E → T E \phi(v):V\rightarrow T_V, \psi(e):E\rightarrow T_E ϕ(v):V→TV,ψ(e):E→TE且 ∣ T V ∣ + ∣ T E ∣ > 2 |T_V|+|T_E|>2 ∣TV∣+∣TE∣>2。
(2)元路径
元路径 P P P是不同类型的边连接起来的不同节点类型的序列。
(3)HIN embedding
输入 G = ( V , E , T , ϕ , ψ ) G=(V,E,T,\phi,\psi) G=(V,E,T,ϕ,ψ),将节点映射到潜在的低维表示空间,同时保留原始的网络结构信息以及语义关联。
作者使用两个真实的HIN检测节点的power-law分布是否也存在不同的元路径。
节点分布计算过程如下:给定元路径 P P P和节点 v v v,首先计算从节点 v v v出发,按照元路径 P P P的模式,能生成多少条元路径。然后计算有多少节点有相同的结果。上述两步操作的结果分别作为横纵坐标值,分布在空间中。例如,对于DBLP和MovieLens 数据集,有如下分布:

从图中可以看出,这些分布是幂律分布。表明了双曲空间可能是HIN嵌入的合适的空间。
HIN中有许多元路径,有些元路径也许不具有幂律分布,但是在本文后续的实验中可以看出,实验结果仍然是有竞争力的。今后的研究还需要对元路径有更细粒度的分析。
幂律分布通俗解释:数据波动非常地大,少数点的数值特别高,大多数的点数值都很低,最大和最小的点之间,可能相差好几个数量级。
这和网络的生长方式有关:网络生长的方式不是随机发生的,而是优先连接。当新的节点加入网络,或者网络中有新的连接产生时,连接度高的节点会比连接度低的节点更有可能得到新连接,这就是所谓的优先连接。
3.2 Hyperbolic Geometry and Embedding
双曲几何是非欧几里德几何,它是通过取代欧几里德第五几何公设(平行公设)而得到的。
双曲空间H的一个关键性质是它们比欧几里得空间扩张得更快,因为欧几里得空间R多项式地扩张,而双曲空间H指数地扩张。

在图4(a)中,每个瓦片在双曲空间中的面积是相等的,但是在欧式空间中随着向边界处扩展,面积逐渐减小为0。
由于这个性质,双曲空间可以考虑为连续树。如图4(b)所示,对于分支系数为b的树,第 l l l层的节点数为 ( b + 1 ) b l − 1 (b+1)b^{l-1} (b+1)bl−1;从根节点出发跳数不超过 l l l的节点数为 [ ( b + 1 ) b l − 2 ] / ( b − 1 ) [(b+1)b^l-2]/(b-1) [(b+1)bl−2]/(b−1)。
节点的数量,随着节点到根节点距离的增加而指数增长,这和双曲空间是很相似的,都是指数型增长。在双曲空间中,树结构类型的数据可以被天然地嵌入到2维双曲空间中。
给定第 l l l层的一个节点,它可以被表示在双曲空间距离源点 d H ∝ l d^H\propto l dH∝l的球面上,分支系数 b b b可用双曲空间中的常曲率 K = − l n 2 b K=-ln^2b K=−ln2b表示。
如上所述,节点的数量随着节点到根节点距离的增加而指数增长,树中节点的分布也就服从幂律分布。呈幂律分布的数据,适合于建模在双曲空间中(Krioukov et al. 2010)。
双曲空间不能等距同构到欧式空间,很难做。有学者提出了一些双曲空间的等价模型,例如Poincar´ e disk (ball) model,Poincar´ e half-plane model, Beltrami-Klein model, hyperboloid model 。作者使用了Poincar´ e ball model,因为该模型可适用于基于梯度更新的优化。
设 D d = { x ∈ R d : ∣ ∣ x ∣ ∣ < 1 } D^d={\{x \in R_d:||x||<1\}} Dd={x∈Rd:∣∣x∣∣<1}为开放的 d d d维单位球。Poincar´ e ball模型用多个 D d D^d Dd和如下所示的黎曼度量张量(Riemannian metric tensor) g x D g^D_x gxD表示:
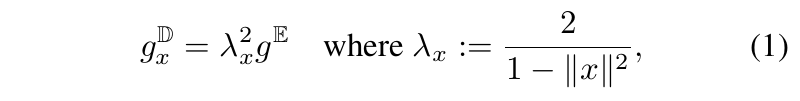
其中 x ∈ D d , g E = I x\in D^d, g^E=\bold I x∈Dd,gE=I表示欧几里得度量张量。Poincar´ e模型是保角的,也就是说,模型中两个双曲线之间的欧几里得夹角和它们之间的双曲夹角相等,因此可用于基于梯度的优化方法。
3.3 HHNE模型
给定异质图 G = ( V , E , T , ϕ , ψ ) , ∣ T V ∣ > 1 G=(V,E,T,\phi,\psi), |T_V|>1 G=(V,E,T,ϕ,ψ),∣TV∣>1,目的是学习到节点表示 Θ = { θ i } i = 1 ∣ V ∣ , θ i ∈ D d \Theta={\{\theta_i\}^{|V|}_{i=1}}, \theta_i\in D^d Θ={θi}i=1∣V∣,θi∈Dd。通过促进节点 v v v和其邻居 c t ∈ C t ( v ) c_t\in C_t(v) ct∈Ct(v)的相似性(t为类型),实现对网络结构的保留。
使用元路径指导的随机游走,为每个节点获得异质邻域。给定元路径模式 P P P,在第 i i i步的转移概率计算如下:
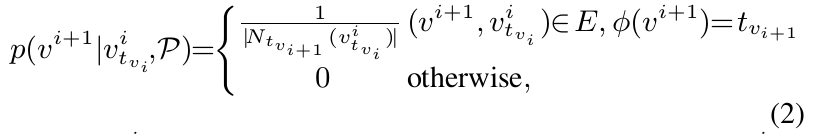
其中 v t v i i v^i_{t_{v_i}} vtvii是类型为 t v i t_{v_i} tvi的节点, N t v i + 1 ( v t v i i ) N_{t_{v_{i+1}}}(v^i_{t_{v_i}}) Ntvi+1(vtvii)是节点 v t v i i v^i_{t_{v_i}} vtvii的类型为 t v i + 1 t_{v_{i+1}} tvi+1的邻居节点。
使用节点在Poincar´ e ball 模型中的距离,来衡量节点间的相似度。给定节点嵌入表示 θ i , θ j ∈ D d \theta_i, \theta_j\in D^d θi,θj∈Dd,距离计算如下:
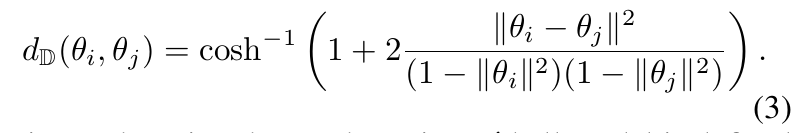
使用概率模型,衡量节点 c t c_t ct是节点 v v v的邻居的概率:
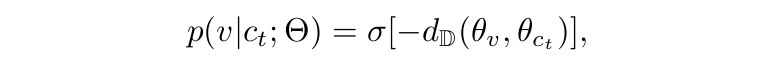
其中 σ ( x ) = 1 1 + e x p ( − x ) \sigma(x)=\frac{1}{1+exp(-x)} σ(x)=1+exp(−x)1。模型的目标函数就是最大化下面的概率:
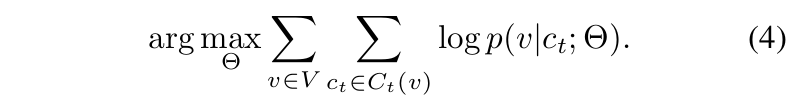
作者还利用负采样技术,以实现更有效的优化。在HHNE模型中,对于给定的节点 v v v,我们希望最大化 v v v和邻居节点 c t c_t ct的相似度,同时最小化 v v v和负采样节点 n n n的相似度。因此,(4)式被重写为下式:
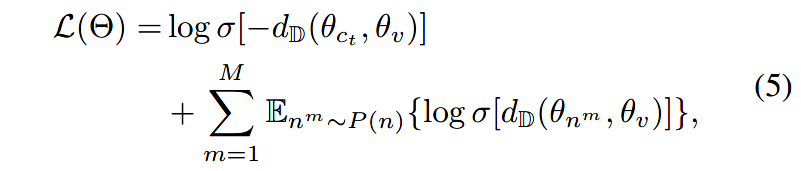
3.4 优化
由于Poincar´ e ball 模型有着Riemannian manifold structure,所以反向传播的梯度是黎曼梯度。也就是说,基于欧几里得的梯度优化,例如: θ i ← θ i + η ∇ θ i E L ( Θ ) \theta_i \leftarrow \theta_i+\eta\nabla^E_{\theta_i}L(\Theta) θi←θi+η∇θiEL(Θ),是无效的优化。
所以,(5)式需要通过黎曼随机梯度下降(RSGD)来优化。 T θ i D d \Tau_{\theta_i}D^d TθiDd为节点嵌入 θ i ∈ D d \theta_i\in D^d θi∈Dd的切面空间。然后就可以计算 L ( Θ ) L(\Theta) L(Θ)的黎曼梯度 ∇ θ i R L ( Θ ) ∈ T θ i D d \nabla^R_{\theta_i}L(\Theta) \in \Tau_{\theta_i}D^d ∇θiRL(Θ)∈TθiDd。使用RSGD,(5)式中的参数按照如下的方式更新:
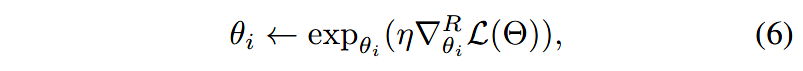
给定 θ i ∈ D d , s = η ∇ θ i R L ( Θ ) \theta_i\in D^d, s=\eta\nabla^R_{\theta_i}L(\Theta) θi∈Dd,s=η∇θiRL(Θ),指数映射函数 e x p θ i ( ⋅ ) exp_{\theta_i}(\cdot) expθi(⋅)表示如下

因为Poincar´ e ball模型是双曲空间中的保角模型,所以黎曼梯度 ∇ R \nabla^R ∇R可以通过,对欧几里得梯度 ∇ E \nabla^E ∇E进行尺度变换得到:
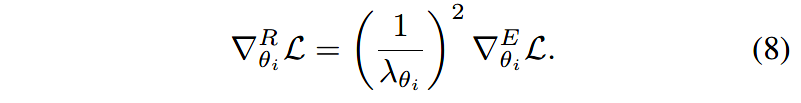
对(5)式求导的结果如下,迭代地使用(9)(10)式更新模型参数:


其中
α
=
1
−
∣
∣
θ
c
t
∣
∣
2
,
β
=
1
−
∣
∣
θ
u
m
∣
∣
2
,
γ
=
1
+
2
α
β
∣
∣
θ
c
t
−
θ
u
m
∣
∣
2
\alpha=1-||\theta_{c_t}||^2, \beta=1-||\theta_{u^m}||^2, \gamma=1+\frac{2}{\alpha\beta}||\theta_{c_t}-\theta_{u^m}||^2
α=1−∣∣θct∣∣2,β=1−∣∣θum∣∣2,γ=1+αβ2∣∣θct−θum∣∣2;
m
=
0
m=0
m=0时,
u
0
=
v
u^0=v
u0=v;
I
v
[
u
]
I_v[u]
Iv[u]是指示函数,表示
u
u
u是否为
v
v
v。
4 实验
数据集:DBLP、MovieLens。
实验任务:网络重构;链接预测;可视化。
对比方法:
(1)同质网络嵌入方法:DeepWalk、LINE、node2vec
(2)异质信息网络嵌入方法:metapath2vec
(3)双曲同质网络嵌入方法:Poincar´ eEmb
实验结果:
(1)网络重构实验结果:

(2)链接预测实验结果:

(3)DBLP数据集可视化结果如下:

5 总结
本文在双曲空间中研究了HIN的嵌入学习问题,提出了HHNE模型,是第一个进行此项研究的文章。
文章使用了节点在双曲空间中的距离,作为相似度度量。既满足三角不等式,又保留了HIN中的传递信息。并使用了黎曼随机梯度下降方法优化模型。
实验表明了HHNE超越了state-of-the-art,并且证明了该模型能发现HIN中的隐含层级信息。尤其是在MoiveLens上的网络重构的实验结果,居然有的高达99%多。
而且当嵌入表示的维度很小的情况下,HHNE模型也能表现出很好的效果。这说明了当空间维度小时,双曲空间有着很强的建模能力。
这篇文章的研究前提是,定义的元路径在HIN中是呈幂律分布的。少量的不满足幂律分布的元路径的存在,并不会对结果产生较大影响。今后的研究还需要对元路径有更细粒度的分析。

























 8273
8273











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








