用矩阵来解最小二乘法,借助MATLAB求解方程。
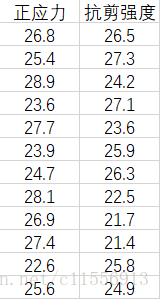
材料的抗剪强度与材料承受的正应力有关。对某种材料试验的数据如下:
假设正应力的数值是精确的。
设一元线性回归方程为y=kx+b。
建立矩阵:
y =
26.5000
27.3000
24.2000
27.1000
23.6000
25.9000
26.3000
22.5000
21.7000
21.4000
25.8000
24.9000>>X=[x,ones(12,1)]
X =
26.8000 1.0000
25.4000 1.0000
28.9000 1.0000
23.6000 1.0000
27.7000 1.0000
23.9000 1.0000
24.7000 1.0000
28.1000 1.0000
26.9000 1.0000
27.4000 1.0000
22.6000 1.0000
25.6000 1.0000
根据公式算出系数k, b。
MATLAB计算程序:
clear
clc
a=xlsread('D:\CSDN\MATLAB\shuju1.xlsx');
x=a(:,1); %正应力数据
y=a(:,2); %抗剪强度数据
C=[x,ones(12,1)]'*[x,ones(12,1)]; %计算C
B=(C^-1)*[x,ones(12,1)]'*y; %计算B
k=B(1,1) %取出k
b=B(2,1) %取出b结果:
k =-0.6861
b =42.5818
这就是一元线性回归方程k, b的最佳估计值,现再求出上述估计量的标准差。
将最佳估计值代入误差方程
>>v=y-(k*x+b)
v =
2.3051
2.1446
1.4458
0.7096
0.0225
-0.2846
0.6643
-0.8030
-2.4263
-2.3833
-1.2765
-0.1182
因为是等精度测量,测得数据y1,y2,…,yn的标准差相同,为
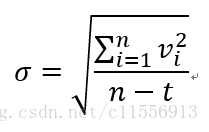
t 为估计量个数。
>>q=sqrt((sum(v.^2))/(12-2)) %计算标准差
q =1.6397
为求出估计量k, b的标准差,首先需要求出不定乘数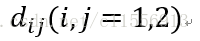
可得估计量的标准差为
>>c1=(C^-1)
>>qk=q*sqrt(c1(1,1))
qk =0.2499
>>qb=q*sqrt(c1(2,2))
qb =6.5065
MATLAB的全部代码:
clear
clc
a=xlsread('D:\CSDN\MATLAB\shuju1.xlsx');
x=a(:,1); %正应力数据
y=a(:,2); %抗剪强度数据
C=[x,ones(12,1)]'*[x,ones(12,1)]; %计算C
B=(C^-1)*[x,ones(12,1)]'*y; %计算B
k=B(1,1) %取出k
b=B(2,1) %取出b
v=y-(k*x+b);
q=sqrt((sum(v.^2))/(12-2)) %计算标准差
c1=(C^-1);
qk=q*sqrt(c1(1,1)) %计算k的标准差
qb=q*sqrt(c1(2,2)) %计算b的标准差结果:
k =-0.6861
b =42.5818
q =1.6397
qk =0.2499
qb =6.5065








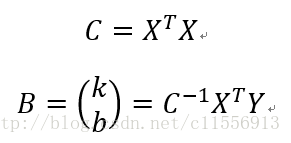

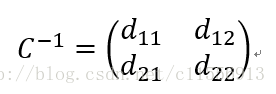















 4647
4647

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








