KDD 2024 | 从几何的视角理解自监督学习中的冗余消除

©PaperWeekly 原创 · 作者 | 张逸飞

单位 | 香港中文大学

研究方向 | 图数据挖掘

本文算是自己博士期间在 Self-supervised learning（SSL）方向上的又一次探索，作为一个 2020 年入学的 Ph.D., 见证了 SSL 由辉煌的时刻（SimCLR，BalowTwin，MoCo，MAE）逐渐转向了 LLM。这次的工作也为博士生涯划上一个圆满的记号了。

非常荣幸的是，在文章 online 的当天，我们这篇自监督学习的文章得到了来自 Balow Twin 作者的邮件（Yann LeCun 也是作者之一），在邮件中，Stephane 赞许了我们的贡献，并建议了一种基于我们方法的新自监督学方式，并邀请一起合作探讨。

Stephane 建议的这个形式，实际上与我的合作者 Hao Zhu 的发表在 NeurIPS 2022 文章基本一致，感兴趣的可以看这里：

https://zhuanlan.zhihu.com/p/570195261

虽然方法一致，但是文章聚焦于图数据，这里不经感叹领域差距还是有点大，而没有收到广泛关注。

背景与动机

为了方便大家的理解，我一般做科普文章，不太纠结于技术细节，希望尽可能把复杂的事情给简单化。我会着重强调动机与为什么方法可以有效的解决。在意细节的朋友们，欢迎阅读论文。

1.1 自监督学习基本范式

在了解我们要解决什么问题，和如何解决之前，我们先看一下自监督学习的一个基本范式，绝大多数自监督学习包括（SimCLR，MoCo，Balow Twin，MAE）其实都是这个损失函数框架下的特例。通常 SSL 的损失函数包含下面两项

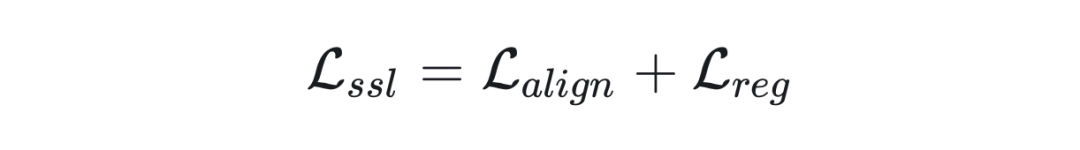
这里第一项我们称之为对齐项（Alignment）。这项是干什么呢？这一项的作用实际上为了帮助 SSL 能够学习到有用的而设计的。在大多数模型中我们使用欧式距离。

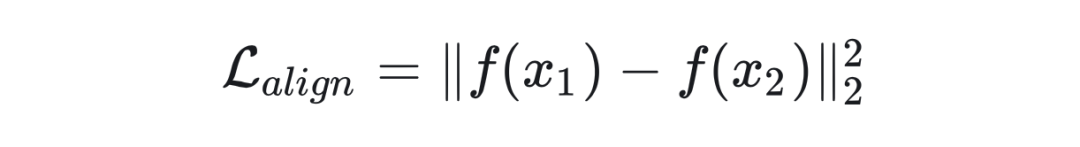
那么为什么说这个损失函数能够让模型学习到有用的特征呢？我又要使用下面这张图了

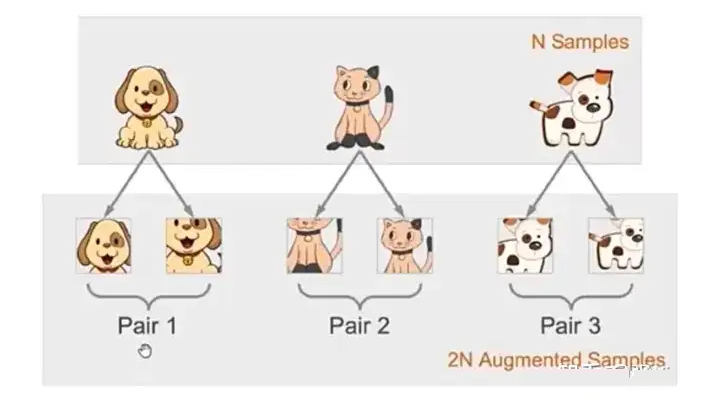
▲ 图0

如上图 1 所示, 我们通过添加扰动的方式对原始的数据进行随机的数据增强, 得到的图片并不影响人识别出来（e.g., 我们总是能认出这是只猫或狗）。这就意味着存在所谓的不变性知识（Invariant Knowlege）或者说是人察觉到本质特征。

而 Alignment Loss，实际上就是优化数据之间的距离来，来强迫模型认为来自同一样本的不同数据增强是一样的，进而提取所谓公共的部分或者是说是本质特征。

这就好比俗话说的：透过现象看本质，当你能摒弃冗余，看到本质，你就学会知识了。这就如同人类自我感知世界的时候：通过观察各种各样的事物来逐渐归纳提取出相同点。

那么一个问题来了，那么在自监督学习，我们只要 Alignment 好不好？这肯定不行了，为什么呢？？

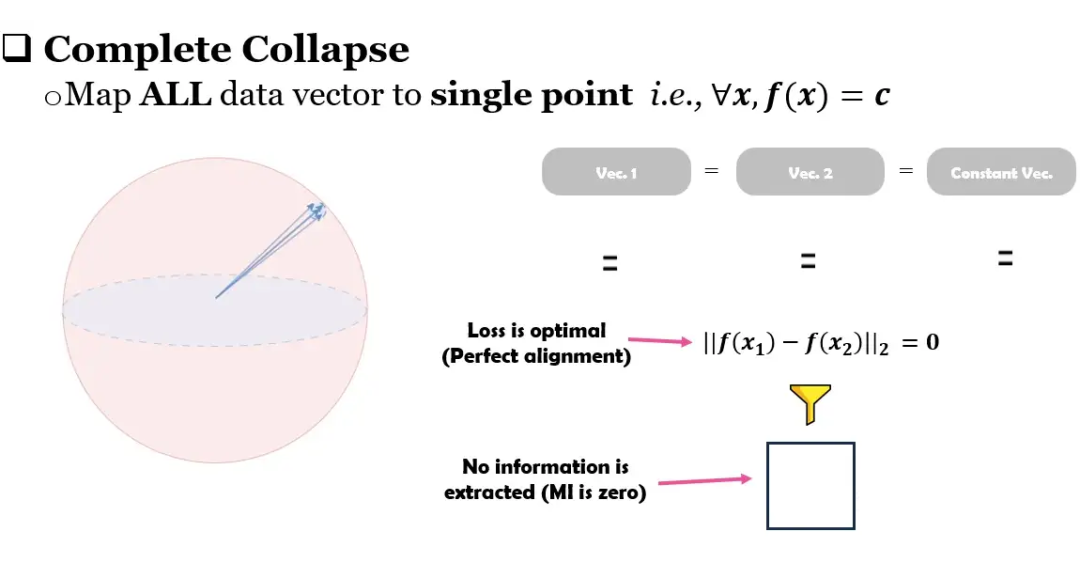
▲ 图1

这里借用我毕业论文中的一张图来说明，一句话概况就是只有 Alignment 会让模型收敛到平凡解。

什么是平凡解呢，一个最简单的例子就是，不管模型的输入是什么，或者说对于所有的输入，模型的输出都是一个常数向量（i.e.,），这样的话 alignment 就一直是最优，一样的常数的距离是 0（完美对齐）。但是没有任何可用的信息被保留。

另外一种情况平凡解不那么平凡，我不塌陷到一个点上，我塌陷到某个子空间内。虽然没有完全的坍塌，但是这也使得区别不同嵌入变的困难，因为多一个维度会让空间变的更加的稀疏，向量之间并不拥挤，更容易让下游任务的分类器来区分不同的嵌入从而获得更好的泛化性。

用个更通俗易懂的例子就是，假如想造楼房，老板给你拨款了 1000 万预算去建房子，你小子贪污偷懒，就花了 1w 块，这尼玛建出来的不是豆腐渣工程么？

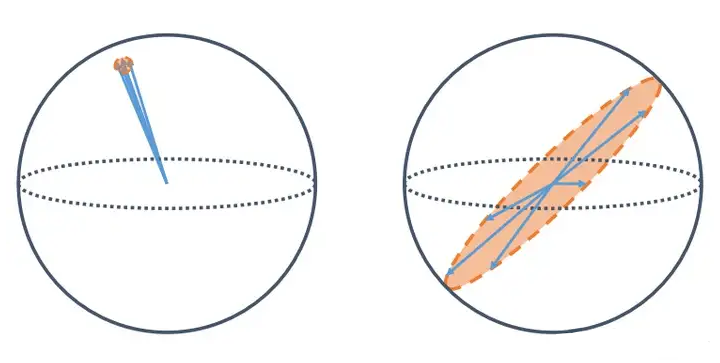
▲ 图2

所以为了避免这些情况，所以在 Alignment 的基础上，各种方法们，都不约而同的，无论有意无意的，设计了另外的 Loss 来防止这种事情发生。这就是我们说的正则项 Loss 

总结来说，一个自监督学习的基本范式实际上干了这么两件事：

• 提取有用特征

• 避免平凡解，也就是我们说的维度塌陷（Dimensional Collapse）

方法论

在介绍我们的 Idea 之前，我们先看看现有的工作是怎么搞的。首先我们看看 SimCLR。

2.1 SimCLR

SimCLR 实际上说的是一系列对比学习工作，他们的共同点就是利用所谓的 InfoNCE 损失函数：

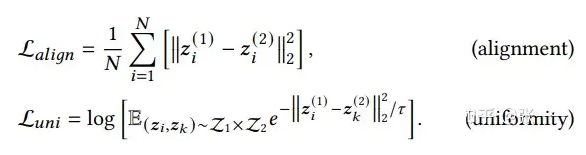
那这个损失函数是如何避平凡解或者说维度塌陷呢？InfoNEC 实际起到了下面的作用。

本质上，维度塌陷就是所有的点都聚集在一起。为了避免这一点，除了让同一个数据的不同 Augmentation 尽可能的接近（也就是我们所说的正样本），我们额外的我让不同数据之间越来越远不就行了？这样数据不就散开了。

所以 InfoNCE 的正则 loss 就是让任意两点之间的距离越来越远避免维度塌陷。

但是不知道大家有没有发现，虽然可以有效避免塌陷在一个点的这个情况，这个做法其实不能避免图 2 中的情况，我们还是会塌陷在一个子空间。不难看出不同数据之间也散的挺开的呀。

这就引出了另一个解决方案，也就是 balow Twin 所要干的事情。

2.2 Balow Twin

上面说了 SimCLR，不能避免图 2 中的情况，那怎么办呢？

我们知道一个特征矩阵所处的空间的维度，实际上是由他的矩阵的秩（Rank）所决定。或者说是这个矩阵非零的特征值所决定。而在这个空间中特征散的开不开或者说均匀不均匀是由特征值的大小决定。所以就有图 3

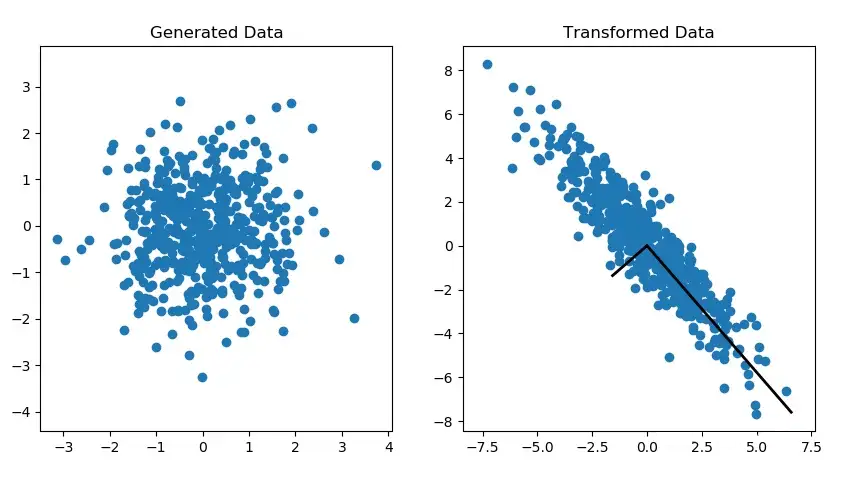
▲ 图3

图 3 中的第一幅图，其实就是 2 个方向上的特征值差不多（平衡），而第二幅图，有一个特征值比较小（不平衡）。

因此为了让特征尽可能的充满整个空间，实际上我们追求的特征值分布是 Isotropic 和 Full Rank 的特性。也就是下图中情况 1

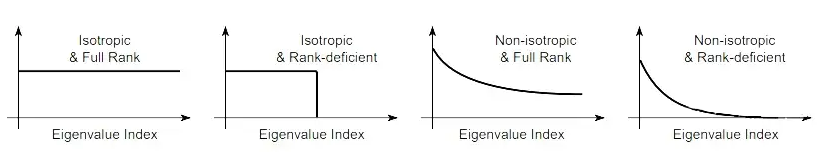
▲ 图4

Isotropic 就是非 0 特征值要均匀分布（uniform distribution）

Full Rank 就是不要有 0 特征值（特征不在某个子空间）

所以基于这样假设的自监督学习实际上就是下面这个有约束的优化问题。

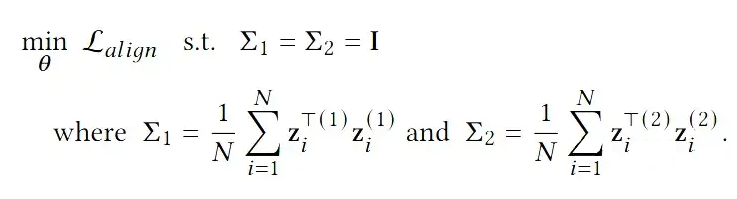
▲ 公式1

通俗的解释是，在满足协方差矩阵是 Identity Matrix 的同时，最小化 Alignment Loss。通常这个问题不是很好解。一般会转化成他的无约束等价形式

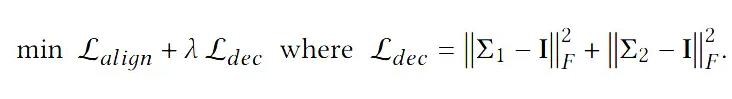
▲ 公式2

这样就变成了 BalowTwin 的形式，也就是我们文中所提到的 Soft Decorrelation的形式。

这里需要注意的是，公式 2 是公式 1 在最优解上是等价的。

但是由于我们使用的梯度下降的方式进行优化，在我们结束训练的时候，我们是无法保证正则项的 Loss 是 0，也就是说我们实际上没有达到 ，也就是 Full Rank 和 Isotropic，他可能是图 4 中的任意一种。

这就说明了利用梯度下降的优化过程中, 约束是不等价的, 也就是叫 Soft Decorrelation 的原因。

那么问题来了，我们怎么能尽可能的保证等价呢？这就引出了本篇文章的重点，从 Geometry 的角度看待这个问题。

Geometry角度来看待Soft Decorrelation

首先，我们的目的是让协方差矩阵尽可能的接近单位矩阵，因此我们需要某种“距离”这个度量协方差矩阵与单位矩阵的远近。

我们观察到公式 2 中的正则项实际是基于某种几何度量来实现的，也就是我们常用的 Frobenius Norm。这时候我猜有朋友会问了，这不是个 Matrix Norm 么？？这咋是距离啊？我读书少你别骗我啊。

没错，这确实是 Matrix Norm，不过 Frobenius Norm 也确实是个距离函数。这里就要提到本论文的核心 Bregman Divergence。

3.1 Bregman Divergence

定义我就直接贴论文原图了：

▲ Bregman Divergence

想深入了解的可以看看这个问题下的回答：

https://www.zhihu.com/question/22426561

这里你只需知道，BMD 是一个度量正定矩阵之间距离的 Divergence，定义 4.1 是他的一般形式，他的具体形式是由一个任意一个严格的凸函数 所决定。不同的 会产生不同 BMD，性质也是由 所决定。

Frobenius Norm 实际上就是 BMD 的特例，其凸函数 ，不信的朋友们可以自己推一下试试。

当 ，BMD就变成著名的 KL Divergence 了（不过这是 Matrix 版本的 KL 我们也叫他 Von Divergence，大家常用的是 Vector 版的 KL，Vector 版的 KL 可以给由 Bregman vector divergence 导出），还是不信的朋友可以自己试试。

理解到这，我相信大家都有点猜出来了，既然 Frobenius Norm 性质不够好，他不是 Bregman Divergence 么，咱给他换个性质好的凸函数 不就完事儿了！！

只能说英雄所见略同，我就是这么干的，虽然文章中我吹的神乎其神，实际我就找了一个性质好的凸函数 ，下面就请出今天的主角 LogDet Divergence！

3.2 LogDet Divergence

我先抛出 LogDet Divergence 的形式，后面我会着重强调，为什么这个 BMD 的性质会好，更适合 SSL。

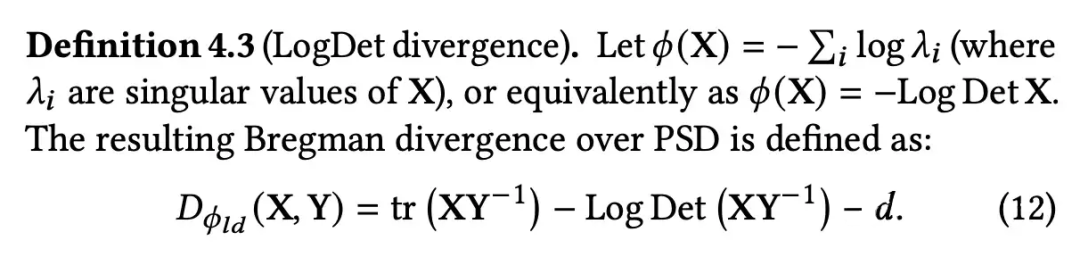
▲ LogDet Divergence

首先我们看定义，在 LogDet Divergence 中， 

既然是 Geometry View，为了比较不同 BMD 之间的性质，我们可视化并比较与每个距离的几何形状（球）。由于 BMD 测量任意正半定（PSD）矩阵与单位矩阵之间的距离，因此我们以单位矩阵为中心描绘每球。关于球的定义如下：

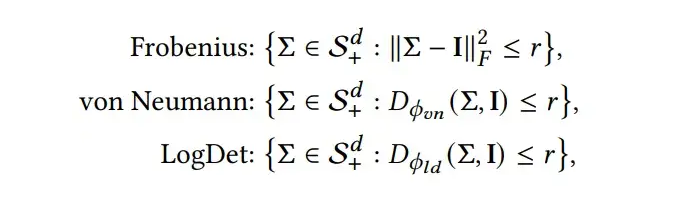
为了方便可视化，我们定义 是只有对角线上有值的半正定矩阵，由于这种矩阵的对角线上的值，实际上就是矩阵的特征值，因此 ， 而不同球的样子如下图所示。

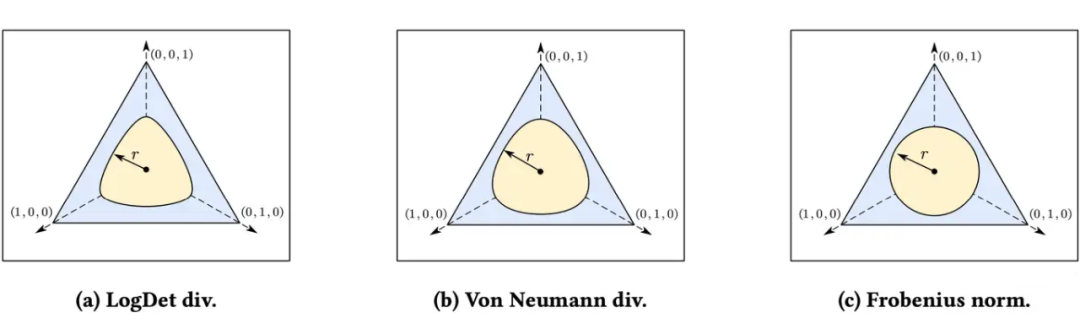
有朋友会问了，看上去确实长得不一样，但有啥优势与好处呢？

观察到 LogDet 和 Von Nemann 点到中心的距离不是固定的，点越靠近坐标轴，比如（0, 0，1）这种点的时候，他的距离值就越大。而 Frobenius 的距离保持一致。

这说明什么呢？实际上这就告诉我们了，如果我们利用 LogDet 来做距离度量的时候，他会在靠近（0, 0，1）的地方产生更大的惩罚梯度（因为你把距离当 loss 优化，距离大 loss 就大，产生的梯度就大）。

这就意味着这在模型训练的时候，有一个无形的推手，来推着你的解远离坐标轴上的点，实际上就是某些维度为 0 的解。

细心的朋友不难发现，这不是就是避免了所说的维度塌陷嘛！！这种远离 0 的解，不就是保住了 Full Rank 嘛！！

可能有又有朋友问，那为啥不用 Von Nemann 呢，原因也很简单，计算 Von Nemann 的开销太大了。LogDet 可以被快速计算，且梯度稳定，Von Nemann 不行，具体感兴趣的朋友，欢迎来看 paper。里面有解释。

讲到着，我猜还有朋友不能理解，为啥 LogDet 就能保证 Full Rank 呢？？我们直接看公式：

我们主要看 Eigenvalue form，简单来说，主要是因为 LogDet 的数学表达式中有 的存在，相比起只含有 的 Frob Norm 来说，当 的时候，LogDet Div。就会无穷大，而 Frob Norm 不会，他还是会按照特征值的大小来分配梯度，大的特征值越大，小的越小。

因此，这就说明了，当我们利用 logDet 来松弛公式 1 中的原问题，我们保证 Full Rank 的约束是一直存在的！

为什么？因为一旦出现 0 的特征值，惩罚梯度就会无限大，

这就好比，一旦出现或者快要出现特征值 0 这个逆子解，LogDet 爸爸就会一巴掌把他扇回正轨。

讲到这里，基本上方法与逻辑就全部结束了。

细心的朋友会发现，等等等，Full Rank 保住了，那 Isotropic 呢？？？你不是要图 4 的 1 么，你怎么把 Isotropic 吃了。公式 1 虽然难解，但是还是可以解的啊，大不了老子不用 SGD 去优化。

这是个好问题，但朋友肯定不是老粉。

相信读过我上一篇 SFA 科普文的朋友，都知道追求完美的 Isotropic 是不明智的，因为信号中有噪声，完美的 Isotropic 是会放大噪声的！！所以追求图 4 中 3 就好了，具体可以了解这篇文章 （如果感觉有帮助记得 cite 我们哦）。

实验

一些实验结果我就放在下面，我在科普文中一向淡化实验部分，不然就有点像写实验报告了，我这里放个 Image 的实验。

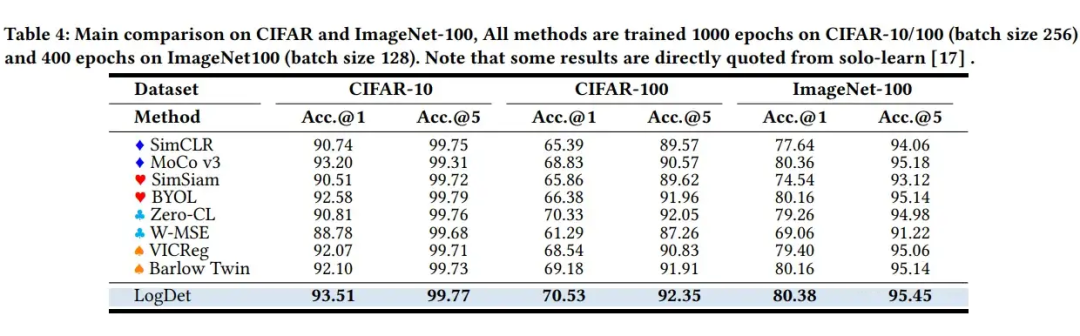
更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·

·