神经网络基础

神经网络基础（王木头学科学）

通过多种指标建立函数模型

需要的变量很多，每一个维度代表一个变量

函数值y的大小就是我们判断是否值得购买的依据，每一个变量的系数w1,w2,w3…wn,（权重系数）都决定了这个维度的数据对最后函数值的贡献程度,b则决定了这个阈值的偏移程度（偏置系数）

支持向量机

对于一个新来的数据，我们就可以针对他在分界线的那一边判断他属于哪一类，如果把这个交给程序，程序要将这个数据带入到函数中，计算出它的函数值，大于零为一类，小于零为另一类。这个过程在机器学习里面叫做决策或者是预测。
机器学习中最难的是要找到最好的分界线，找这个分界线就是一个训练学习的过程。和贪心算法动态规划法不同，不需要每次来了新的数据都需要进行同样复杂度的计算，而是先进行异常复杂的训练和学习，然后再面对新数据时，只需要进行简单的运算就可以达到目标。

需要一个分界线好坏的判断标准。

只是对已知的数据来说是最好的分界线，但不一定对未来其他数据预测都准确。
要引入额外的公设，作为选择判断的标准，来选择最好的分界线：

1、间隔最大最好

分界线到数据的间隔越大越好，可以为新数据带来更多的容错空间
距离表示为：函数值的绝对值除以权重系数的L2范数（将函数值进行L2范数的修饰——SVM）。
这里的权重系数没有偏置系数b。
L2范数可以理解为勾股定理在更高维度上的扩展，也就是对向量里的每个分量进行平方在开放的运算。

这里的间隔指的是所有变量到分界线距离中的最小距离，这里的最小距离就代表了分界线到数据的间隔，M（W）就代表间隔函数，输入不同的系数时，找到不同的间隔值，我们需要找的是让函数M（W）最大的那一组系数w1.w2,w3…wn。

2、概率最大最好

通过sigmoid函数将函数值缩放到0~1之间，将修饰后的函数值看成一个概率值，表示在给定系数W条件下（这一组系数就是我们需要求的那个最好的分界线的系数），随机变量等于某一个数据时的概率，这两个概率就分别代表了某一个数据是当前属于这两类的可能性

一类的函数值大于零，直接带入sigmoid函数得到的就是当前类的分类概率；一类的函数值小于零，要先对函数值取负数，再进行sigmoid操作，然后得到的就是另一类的分类概率。概率值越大，表示这个数据是当前分类的可能性越大。
让所有的数据对应的概率值同时最大最好（更准确的说法是似然值最大，这里变动的不是随机变量X，而是条件W）概率值同时最大应该是相乘的关系，我们要找的就是上图红框里面的表达式取最大时系数W的取值。（可以用log将它变成相加的模式）

3.方差最小最好

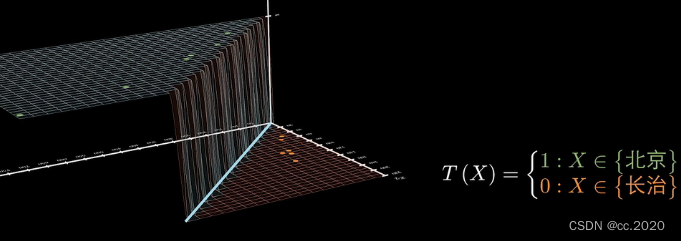
上面是理想状态下的分类情况，实际上会有白噪声和误差会对函数造成影响，我们用ε来表示T函数叠加了一个噪声，他的输出值仍然是会接近0和1，不再是完美的非0即1了，

这时候我们将1+ε和0+ε替代为sigmoid函数，用它来表示受到噪声干扰后的T（x）函数

这时候sigmoid函数值与他们在T（x）函数中取值的偏差，就是叠加噪声后的误差ε，最好的分界线就是这个误差越小越好。换另外一种表达是就是方差越小越好。

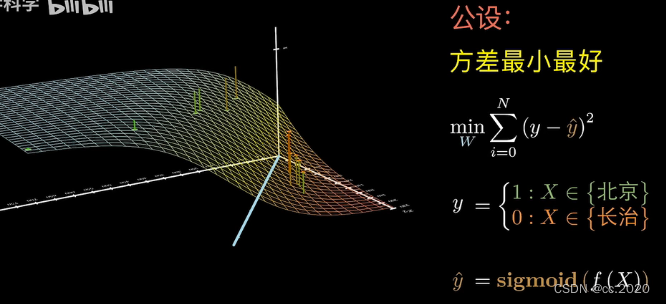
最后是将所有数据的方差都加起来让它取值最小的那组系数表现最好，y就是绝对正确的打的标签。

公设不同，最后的分界线的结果也不相同。

哪一种公设最好具体问题具体分析。

计算最好分界线下对应的系数

几乎不可能直接求出解析解，找到什么样的算法，能更快更好的找到判断标准的数值解（算法几乎就是在指梯度下降法）

把x的四次项增加进来，就会有三个弯

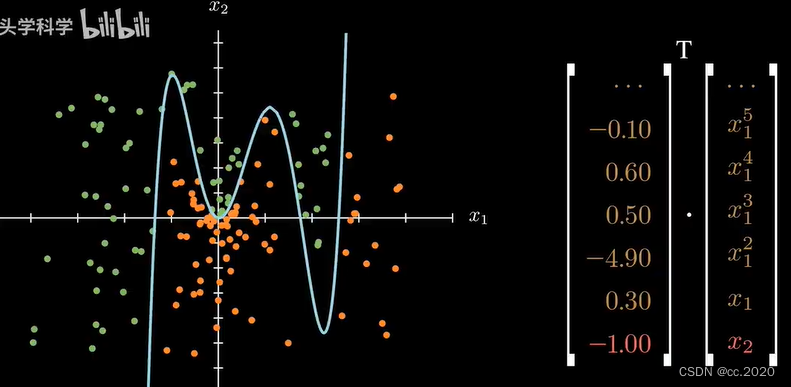
把x的五次项增加进来，就会有四个弯
随着次数增加，模型的复杂程度会大大提高。

这样的曲线可以是分类问题，也可以还是回归问题拟合问题（这里拟合和回归差不多，拟合或者回归出这样一条曲线，那么给定任何一个x1数据，都可以预测出对应的x2的数值，同样的模型就在完成预测的工作，而不是分类的工作）
这里只考虑分类的问题。

神经网络就是提高模型复杂程度的一个方法。

全连接神经网络

神经网络任意一个神经元都会和上一层下一层所有节点相连

这个结构本来就是一个线性方程（如下）

结果z还要进行一次函数运算（激活函数），才会输出到下一层（下图中的sigmoid函数只是负荷要求的函数之一）

激活的过程并不会在神经网络的图示中表示出来，而是用神经元统一表示。

先讨论二维数据的情况。神经元的数量在不断增加，模型的复杂程度也会变大。
输出结果的曲面上图所示。
分界线（x1,x2平面上的红色直线）

上图是没有激活函数的情况，输出结果的曲面只会是一个平面。
中括号的上标来表示它是神经元的第几层，输入层是0层。第一层的输出结果会作为第二层的输入。增加了一层神经元之后，图像并不会有特别大的变化。
两个输入、两个神经元时，输出结果变成了向量，有多少个神经元，就有多少个分量。激活函数的变量也就变成了用向量进行表示了。表示变量里的每一个分量都要进行一次sigmoid计算，第二层的输入也会相应的变成两个（可以看到分界线已经发生了弯曲）

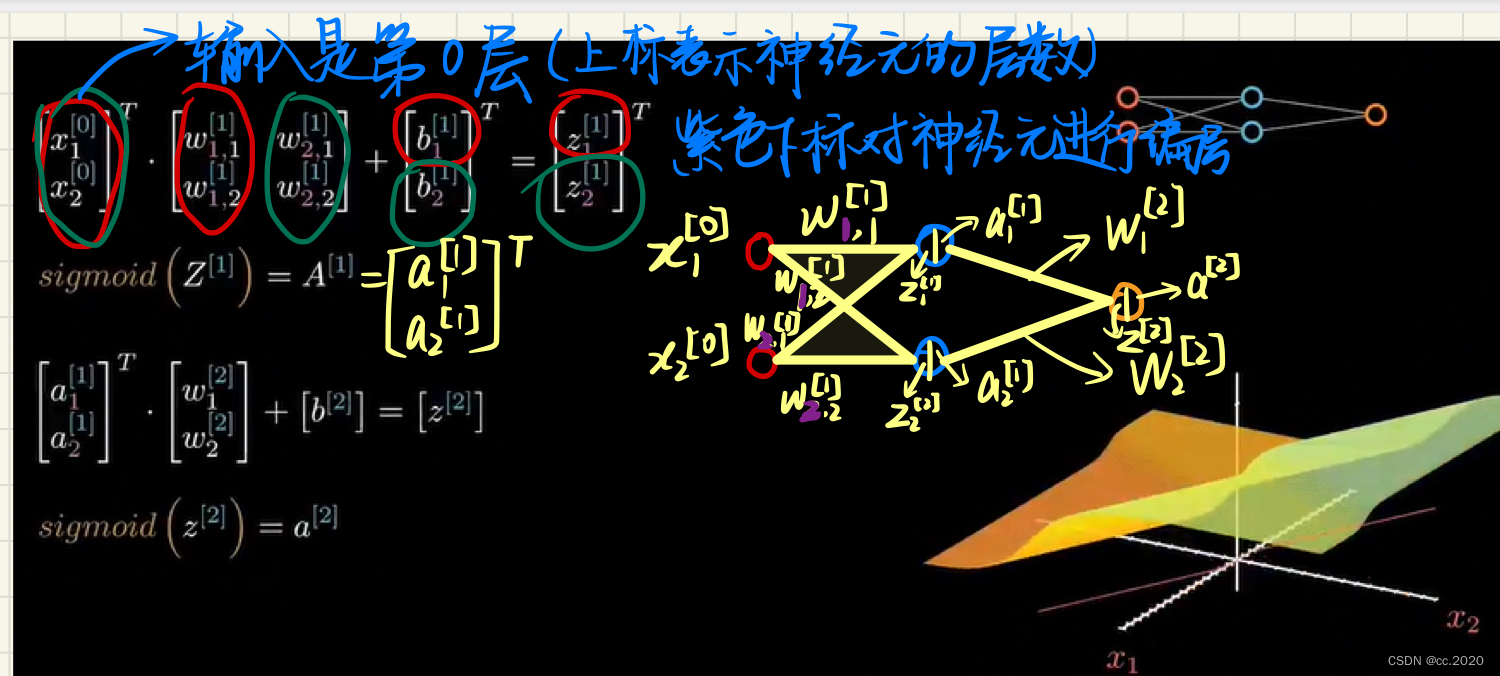
将神经元增加到四个：

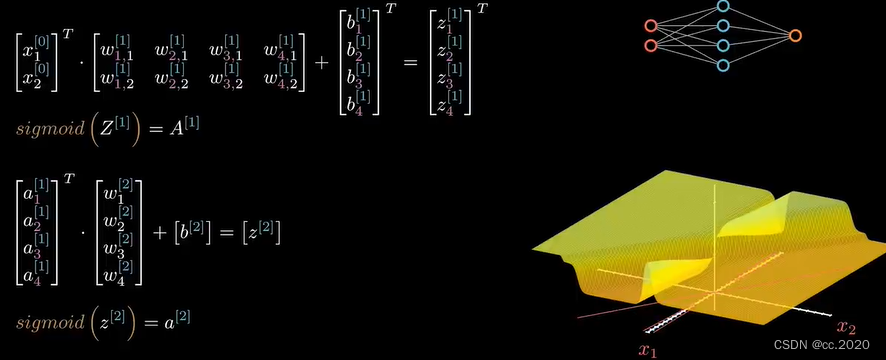
没有激活函数，再多的神经元也没有办法增加模型的复杂性，只会是一个超平面（神经网络的复杂性来自激活函数）。常用的激活函数：

数据是二维的，互相掺杂在一起，很难用直线进行划分，但是如果把他们升维，在更高的维度中，即便用更简单的模型也可以把他们分开。（如下图所示，矩阵操作相当于对向量的一个升维操作，有多少个神经元，就会将数据升到多少维。只要维度够高，就会找到这样一个超平面对数据完成划分）

神经网络不仅可以解决二分类问题，还能够解决多分类问题，每一个节点都是在进行一个二分类判断，是或者不是。激活函数用的是softmax函数。

每一个像素都是数据的一个维度，对上一层即隐藏层（像素维度）进行了抽象，抽象成最后判断的特征。



模型：隐藏层决定
策略：输出层决定
输入层需要对数据进行数据预处理
神经网络的算法就是反向传播，反向传播的关键就是梯度下降法。

上面在已知W,b这两个参数的情况下，输入X，给出Y，这个是正向传播。反向传播就是把正向传播反过来，如果是在训练一个神经网络（即要求得最好的参数W），用来训练的数据是已知的输入输出数据，参数W是我们需要求解的，这就是反向传播。

下面是反向传播：
我们的目的就是找到曲面的最高点，即使得yhat最大的那个W。W就是在系数平面上的投影（黄点）。

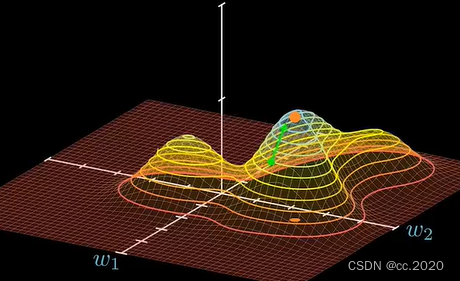
寻找方法：任意一个点都可以求出一个向量，这个向量总是指向上升最快的方向，这个向量在参数平面上的投影叫做梯度。（若是求最大的问题，我们加一个负号转变成求最小的问题）

所有的参数都按照梯度的分量进行调整，调整后的W就代表了参数最好的选择。

η是学习率，属于超参数，不能有神经网络学习训练得到，需要手动进行配置。学习率过小，移动步长短；学习率过大，虽然会很快接近最值点，但是
会在最后反复横跳，无法收敛。
每一个变量的值都要求偏导，得到的结果就是梯度在这个维度上对应的分量。
梯度下降就是把计算出来的梯度（学习率乘以偏导）反向传播到神经网络里面，让所有的W进行更新和修改。

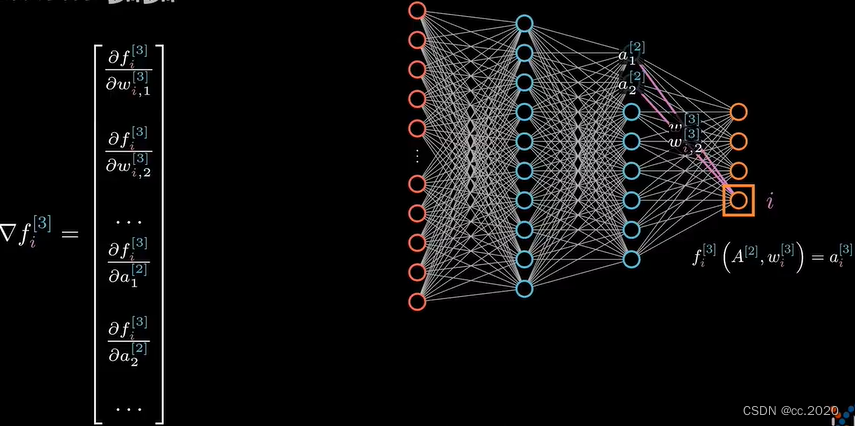
梯度就是对所有的输入变量的维度求偏导，上一层的输出结果a也是输入变量，也要对a求偏导。
对梯度的修改：
1、用梯度的分量可以直接对系数W进行修改。
2、并不能直接对上一层的输出结果A进行修改，只能对更前面的系数进行修改，才能间接达到修改输出结果的目的。

下图是对梯度的修改：

首先是对输出层的系数W[3]修改：
用梯度的分量可以直接对系数W进行修改。修改后的系数如下（对A的修改只能由下面的系数算出之后再对梯度进行修改）：

对隐藏层的系数W[2]修改：
要对前面的系数进行修改，就传到了前一层，对于隐藏层的节点，不是直接求梯度，因为改进自己的系数需要受到输出层的影响；输出层的四个神经元都会对这个节点产生影响，把所有的影响都加起来，如下：
上面对a求偏导，a也是上一层的函数，将a用f来替代（如下图）再乘以用梯度的分量直接对系数W进行修改。（隐藏层的系数W[2]最终结果如下）

对隐藏层的系数W[1]修改：

1、系数W[1]的修改还是会受到第二层W[2]所有神经元的影响。总的影响如下：
/2、用自身梯度的分量直接对系数W进行修改如下：

综合1、2两种影响如下：

最后，他的输入是数据本身，是已知参数，不是变量，所以不需要进行修改。不再需要向前传递，只需要对自己的系数做出相应的修改。

反向传播的越深，学习率的次幂就越高。因为学习率往往是小于1的，所以很可能出现这种情况：神经网络的深度很深，那么低层次的神经元，虽然梯度很可能到最后虽然有梯度传到了这里，但是与学习率相乘以后，会得到一个非常小的数值，可能对系数的修改不会有很多的调整。这就是梯度消失问题