
对比原型网络与原型增强用于小样本分类
引用:Jiang, Mengjuan, et al. “Contrastive prototype network with prototype augmentation for few-shot classification.” Information Sciences 686 (2025): 121372.
论文地址:下载地址
Abstract
近年来,基于度量的元学习方法因其在解决小样本分类问题上的有效性而受到广泛关注。然而,数据的稀缺性常常导致次优的嵌入,从而造成预期类别原型与从支持集中得到的原型之间的差异。这些问题严重限制了此类方法的泛化能力,因此需要进一步发展小样本学习(Few-Shot Learning, FSL)。在本研究中,我们提出了一种对比原型网络(Contrastive Prototype Network, CPN),其由三个部分组成:(1) 提出了对比学习作为辅助路径,用于缩小同质样本之间的距离并放大异质样本之间的差异,从而增强嵌入的有效性和质量;(2) 提出了伪原型策略来解决原型中的偏差问题,通过使用查询集样本生成的伪原型与初始原型结合,获得更具代表性的原型;(3) 引入了一种新的数据增强技术,mixupPatch,以缓解数据样本不足的问题,通过将不同样本的图像和标签进行混合生成增强图像,以增加样本数量。在五个数据集上进行的大量实验和消融研究表明,CPN在与最新解决方案的对比中取得了稳健的结果。
1. Introduction
深度学习1已广泛应用于众多领域,如智能驾驶1和医学诊断2,并受益于数据量的增长和计算性能的提升,从而在某些场景下超越了人类的表现3。然而,由于深度学习是一种对数据需求较高的方法4,其成功受限于标记样本的数量,只有在拥有大量标记样本的支持下,才能超越人类的表现。然而,在获取大量标记样本方面存在一定困难,例如在医疗领域,出于保护患者隐私和安全的需要,很难获得足够的标记样本;此外,标记大量样本既劳动密集又耗时昂贵。以上种种困境导致了深度学习发展的瓶颈。
人类可以通过少量样本快速识别新事物。例如,一个小孩通过媒体只看到一次“大象”的图像,随后便能在大量图片中轻松识别出“大象”。这种人类能力,即学者们所称的小样本学习(Few-Shot Learning,FSL)5,是深度学习所不具备的,这一差距再次激发了对FSL的研究热情。FSL要求模型在有限的标记样本下快速学习并泛化到新类别。因此,模型必须具备快速学习的能力。
元学习3利用先前获得的知识来促进新任务的学习,因此自然适用于FSL5。使用元学习进行小样本分类的方法包括基于数据增强的方法6 7,基于度量的方法3 8 9,以及基于优化的方法10 11。基于度量的元学习因其高效性而受到研究者的广泛关注12。具体来说,这些方法将所有样本映射到一个特征空间中,然后使用相似性度量来计算查询样本与所有原型之间的相似性,以确定查询样本的类别。因此,获得的嵌入函数的质量至关重要。一个好的嵌入函数可以最大化或最小化相似样本或异质样本之间的相似性9。然而,由于数据不足,小样本学习中很难学习到高质量的嵌入。数据不足还会导致预期原型与实际得到的原型之间的偏差,即使用支持集计算的类别原型不够具有代表性3。例如,Vinyals等人提出的Matching Networks (MN)是一种小样本学习中的经典方法8,依赖于支持集和查询集之间的注意力机制进行分类。其工作原理包括使用CNN和LSTM网络提取样本特征,并通过注意力机制计算查询样本与支持样本之间的相似性。然而,Matching Networks需要支持集中有大量样本,因为更多的样本可以生成更准确的相似性匹配。在数据稀缺或样本噪声高的情况下,模型性能可能会受到影响。Few-shot Embedding Adaptation with Transformer (FEAT)提出了一种基于集合到集合函数的嵌入自适应方法,该方法通过学习自适应嵌入函数将小样本数据转化为更鲁棒的表示13。尽管FEAT在嵌入自适应方面有所改进,且可以更好地处理小样本数据,其有效性仍然依赖于支持集样本的质量和数量。当数据稀缺时,嵌入质量可能会受到影响,导致模型无法有效泛化到新类别。Deep Subspace Networks (DSN)14通过子空间来表示类别,更多的样本可以更准确地定义每个类别的子空间,从而提高分类性能。因此,支持集中样本越多,生成的子空间就越准确,模型性能越好。然而,这也意味着在数据稀缺的情况下,DSN的有效性可能会受到限制。
对比学习15的目标是学习一个编码器,使得相似数据的编码结果尽可能相同,不同数据的编码结果尽可能不同。该思想类似于基于度量的小样本学习,其中相似样本在表示空间中的表示更接近,而异质样本的表示在表示空间中更远,从而实现类似的聚类效果。对比学习在计算机视觉中取得了显著成功。MOmentum COntrast (MoCo) 15和简单的视觉表示对比学习框架 (SimCLR) 16在无监督图像特征学习中表现出了强大的性能。因此,本研究通过对比学习和元学习实现小样本学习。
了解决上述难题,本研究提出了一种新的基于度量的元学习技术,称为CPN。CPN主要包含两条互补路径:以原型网络为主路径的对比学习模块作为补充角色。对比学习模块首先以特定形式构建正/负样本对,然后通过最大化/最小化正/负样本对的相似性来增强模型的特征提取能力。对于偏置原型的问题,受Mao等人17的启发,我们为主分支提出了伪原型策略,通过从查询集中选择一些高置信度的查询样本来生成伪原型,并将其与从支持集中提取的初始原型结合,以生成更具代表性的类别原型。对于辅助分支,我们提出了基于数据增强的mixupPatch策略,通过混合不同样本的图像和标签来扩充训练样本的数量,从而缓解数据不足的问题。CPN在五个公开的小样本数据集上进行了评估,结果显示,CPN在域内和跨域场景中都具有很强的竞争力。例如,CPN的准确性比任务依赖自适应度量(TADAM)12高出近10%。
本研究的主要贡献如下:
-
提出了一种互补路径网络结构以实现小样本分类。考虑到对比学习与基于度量的元学习的目标相似,且自监督对比学习不需要引入任何额外数据,因此利用对比学习作为一种无负担的辅助任务来提升分类的有效性。
-
提出了用于原型校正的伪原型策略。该策略选择性地利用查询集中的高置信度样本来生成伪原型,以参与类别原型的校准,使得到的新原型更接近于预期的原型。
-
提出了mixupPatch策略。该策略通过混合不同样本的图像和标签来扩充样本并丰富样本的多样性,不仅在一定程度上消除了基础类别中数据偏差对模型学习新类别的负面影响,而且在面对受损输入时增强了模型的鲁棒性。
-
在五个数据集(miniImageNet、tieredImageNet、FC100、CUB200和Cars)上进行了全面实验,结果显示了CPN的强大性能。
本文其余部分组织如下:第2节回顾了相关工作。第3节介绍了问题设定、整体框架及提出的三个组成部分。第4节介绍了数据集和实验设置。第5节讨论了实验结果及分析。第6节描述了理论与实际意义。最后,第7节对全文进行总结并展望未来工作。
2. Related work
2.1. Few-shot learning
小样本学习旨在从极少的标记样本(通常只有一个或少数几个)中学习,以分类从未见过的样本10。从少量样本中学习的能力是区分人类智能和人工智能的关键。到目前为止,小样本学习已应用于计算机视觉、强化学习等领域,展示了巨大的发展潜力。
基于优化的方法致力于使模型具有强泛化的初始化参数,使其在遇到新任务时能够快速适应。典型方法是模型无关的元学习(MAML)10。该方法旨在通过在多个任务上训练模型,优化初始参数,使其能够通过少量的梯度更新快速适应新任务。具体来说,MAML在元训练阶段进行多任务训练,并通过反向传播优化初始参数。元训练后,模型仅需少量梯度更新即可适应每个新任务。MAML的主要贡献在于其通用性和快速适应能力。由于其模型无关的特性,MAML可应用于回归、分类和强化学习等多种任务。通过优化初始参数,MAML显著提升了模型在新任务中的学习效率,能够在有限数据和少量训练步骤下表现良好。Sun等人提出的元迁移学习(MTL)11,结合了元学习和迁移学习的优势,以提高小样本学习的有效性。MTL首先在大规模数据集上对模型进行预训练,然后在小样本学习任务上进行元训练,调整模型参数以适应新任务。其主要贡献在于高效的迁移和适应能力。通过在大规模数据集上预训练,MTL利用了丰富的先验知识,使模型能够快速适应并在小样本学习任务中取得优异表现。Jia等人提出了一种混合优化的元学习方法Mix-MAML18,旨在提高元学习中的泛化性能。该方法结合了三种技术:数据增强、初始化衰减和分辨率提升。具体来说,数据增强通过随机擦除增加样本多样性,以解决过拟合问题。初始化衰减基于任务梯度生成特定初始化参数,增强模型对新任务的适应能力。分辨率提升则通过提高图像分辨率来捕捉更多特征信息。Mix-MAML方法在不同的网络结构和分辨率上均表现出优异性能。
基于数据增强的方法通过缩放、裁剪和数据生成等手段来增加样本数量,以缓解数据不足问题。Chen等人提出了创新的图像变形元网络(IDeMe-Net)6,解决了1-shot学习问题。该方法结合了变形子网络和嵌入子网络。变形子网络通过融合探测图像和图库图像生成多样化的变形图像,尽管这些图像在视觉上可能不真实,但它们保留了关键语义信息,有助于形成分类器的决策边界。嵌入子网络将图像映射到特征空间并执行1-shot分类。整个网络通过端到端元学习进行优化,使模型能够从极少的样本中学习新的视觉概念。IDeMe-Net的贡献在于其新颖的图像变形框架,能够有效利用图像的变形模式来扩充和多样化训练数据,从而显著提高1-shot学习任务的性能。Zhang等人提出了一种简单而灵活的框架MetaGAN,用于解决小样本学习问题7。该方法通过集成条件生成对抗网络(GAN)增强了现有的小样本学习模型,从而提高了区分真实和虚假数据的能力。该方法通过对抗性训练优化分类器的决策边界,从而增强模型的泛化性。MetaGAN通过利用标记和未标记的数据实现有监督和半监督学习,其有效性通过在各种小样本图像分类基准上的广泛实验得到验证,表现出显著的性能提升。该方法的独特之处在于能够在样本和任务级别有效利用未标记数据,从而为实际应用提供了稳健的解决方案。
基于度量的方法包括三个重要组成部分:用于从样本中提取特征的嵌入函数、代表性的类别原型和用于度量样本间相似性的度量。常见的度量包括欧几里得距离3、余弦相似度8、关系模块9和任务自适应度量12。原型网络(PN)3将所有样本嵌入到特征空间,然后使用支持集样本的平均嵌入向量作为类别原型,最后计算查询样本与每个类别原型之间的距离进行分类。PN使用原型表示,使得分类过程直观且计算效率高。这种简单而有效的方法显著提高了小样本分类性能。关系网络(RN)9引入了关系模块来计算样本和类别原型之间的关系分数。模型首先通过神经网络提取样本特征,然后使用关系模块计算查询样本与支持集样本之间的相似性分数进行分类。RN方法通过关系模块增强了模型的灵活性,使其能够处理更为多样的特征表示。TADAM12是一种创新的小样本学习方法。它引入了任务依赖自适应度量机制,能够在任务层面动态调整度量空间以满足不同任务的需求。具体而言,TADAM使用元学习框架在多个任务上训练模型,并学习适应每个特定任务的度量调整参数。这使得模型能够根据新任务的特性自适应地调整其度量空间,从而提高分类性能。TADAM的主要贡献在于其灵活性和适应性。通过任务依赖的度量调整,TADAM在多样化任务中表现出色,从而显著增强了模型的泛化性和鲁棒性。此外,TADAM不仅在标准的小样本学习任务中表现优异,还在具有显著任务差异的场景中保持高效。因此,TADAM是一种强大且多功能的小样本学习方法,为实际小样本学习问题提供了新的见解和解决方案。Mao等人提出了双原型网络(DPNet)17,其主要包含循环比较模块,用于选择可靠的前景特征,多尺度融合模块,用于捕捉上下文信息,以及原型交互模块,用于将原型与伪原型进行融合。通过这种双原型机制,DPNet能够更准确地表示每个类别,从而提高分类准确性。
2.2. Contrastive learning
对比学习是一种无监督学习策略,其主要目标是从未标记数据中学习有意义的特征表示。对比学习通过最大化正样本对(相似样本之间)的相似性并最小化负样本对(不同样本之间)的相似性来区分类别样本。对比学习的关键组成部分包括正负样本对的构建方式、从样本中提取特征表示的特征提取器、度量样本对相似性的度量方法以及损失函数。常用的相似性度量是余弦相似度,而对比损失函数包括InfoNCE和三元组损失。典型的对比学习方法包括MoCo和SimCLR。
MoCo15是Facebook AI研究团队提出的一种创新对比学习方法,专用于无监督的视觉表示学习。MoCo的核心创新是动态字典和动量更新机制,这些机制提供了更丰富和多样的负样本。具体而言,MoCo构建了一个动态更新的字典,用于存储对比学习所需的负样本。该字典由一个动量编码器生成,并通过编码器参数的指数移动平均进行更新,以确保特征表示的稳定性和一致性。在训练过程中,MoCo采用对比学习策略,最大化同一图像不同增强视图(正样本)的相似性,同时最小化不同图像视图(负样本)之间的相似性。这一设计使MoCo能够从大量未标记数据中学习有用的特征表示,而不依赖于标记数据。实验结果表明,MoCo在多项无监督学习基准上取得了显著的性能提升,尤其是在图像分类和目标检测等下游任务中。MoCo不仅有效解决了对比学习中的关键挑战,而且在无监督学习中具有巨大的潜力。通过引入动量更新机制和动态字典,MoCo显著增强了无监督视觉表示学习的效果,标志着该领域的重要突破。SimCLR是一种高效且简单的对比学习框架,专用于无监督视觉表示学习16。SimCLR通过数据增强(如随机裁剪、颜色失真和旋转)生成图像的不同视图,并使用对比损失函数来训练模型。该方法在特征空间中将同一图像的不同视图拉近,同时将不同图像的视图推远。为提高对比学习的效果,SimCLR在基础编码器(如ResNet)之后添加了一个非线性投影头,将特征映射到对比学习的特征空间。通过在大规模数据集上训练并使用大量负样本,SimCLR在各种无监督学习基准上实现了显著的性能提升,尤其是在图像分类等下游任务中表现优异。SimCLR通过其简单的设计和稳健的性能推动了无监督视觉表示学习的发展。
3. Methodology
3.1. Problem definition
考虑数据集 D total = { ( x i , y i ) , y i ∈ C total } \mathcal{D}_{\text{total}} = \{(x_i, y_i), y_i \in \mathcal{C}_{\text{total}}\} Dtotal={(xi,yi),yi∈Ctotal},其中 x i x_i xi 为样本图像, y i y_i yi 为与 x i x_i xi 对应的标签, C total \mathcal{C}_{\text{total}} Ctotal 为所有类别的集合。表1提供了其他符号及其定义,概述了本研究中相关的关键符号。小样本学习(FSL)将数据集 D total \mathcal{D}_{\text{total}} Dtotal 分为三个不相交的集合:训练集 D train = { ( x train i , y train i ) , y train i ∈ C train } \mathcal{D}_{\text{train}} = \{(x_{\text{train}~i}, y_{\text{train}~i}), y_{\text{train}~i} \in \mathcal{C}_{\text{train}}\} Dtrain={(xtrain i,ytrain i),ytrain i∈Ctrain},验证集 D val = { ( x val i , y val i ) , y val i ∈ C val } \mathcal{D}_{\text{val}} = \{(x_{\text{val}~i}, y_{\text{val}~i}), y_{\text{val}~i} \in \mathcal{C}_{\text{val}}\} Dval={(xval i,yval i),yval i∈Cval},以及测试集 D test = { ( x test i , y test i ) , y test i ∈ C test } \mathcal{D}_{\text{test}} = \{(x_{\text{test}~i}, y_{\text{test}~i}), y_{\text{test}~i} \in \mathcal{C}_{\text{test}}\} Dtest={(xtest i,ytest i),ytest i∈Ctest}。训练、验证和测试集的类别分别为 C train \mathcal{C}_{\text{train}} Ctrain、 C val \mathcal{C}_{\text{val}} Cval 和 C test \mathcal{C}_{\text{test}} Ctest。此外, C train ∪ C val ∪ C test = C total \mathcal{C}_{\text{train}} \cup \mathcal{C}_{\text{val}} \cup \mathcal{C}_{\text{test}} = \mathcal{C}_{\text{total}} Ctrain∪Cval∪Ctest=Ctotal, C train ∩ C val = ∅ \mathcal{C}_{\text{train}} \cap \mathcal{C}_{\text{val}} = \emptyset Ctrain∩Cval=∅, C val ∩ C test = ∅ \mathcal{C}_{\text{val}} \cap \mathcal{C}_{\text{test}} = \emptyset Cval∩Ctest=∅, C train ∩ C test = ∅ \mathcal{C}_{\text{train}} \cap \mathcal{C}_{\text{test}} = \emptyset Ctrain∩Ctest=∅。
表1:本文中使用的符号和含义。
| 符号 | 含义 |
|---|---|
| x i , y i x_i, y_i xi,yi | 第 i i i个样本的图像和真实标签 |
| C \mathcal{C} C | 类别集合 |
| D \mathcal{D} D | 数据集 |
| S \mathcal{S} S | 支持集 |
| Q \mathcal{Q} Q | 查询集 |
| T \mathcal{T} T | 任务/回合 |
| f θ f_\theta fθ | 由 θ \theta θ参数化的嵌入函数 |
| P i \mathcal{P}_i Pi | 类别 i i i的支持集原型 |
| P q i \mathcal{P}_q^i Pqi | 类别 i i i的查询集原型 |
| p i p_i pi | 样本属于类别 i i i的概率 |
| α , β , λ , μ , κ , τ \alpha, \beta, \lambda, \mu, \kappa, \tau α,β,λ,μ,κ,τ | 加权因子 |
| ( P os , N eg ) (P_{\text{os}}, N_{\text{eg}}) (Pos,Neg) | 正样本和负样本对 |
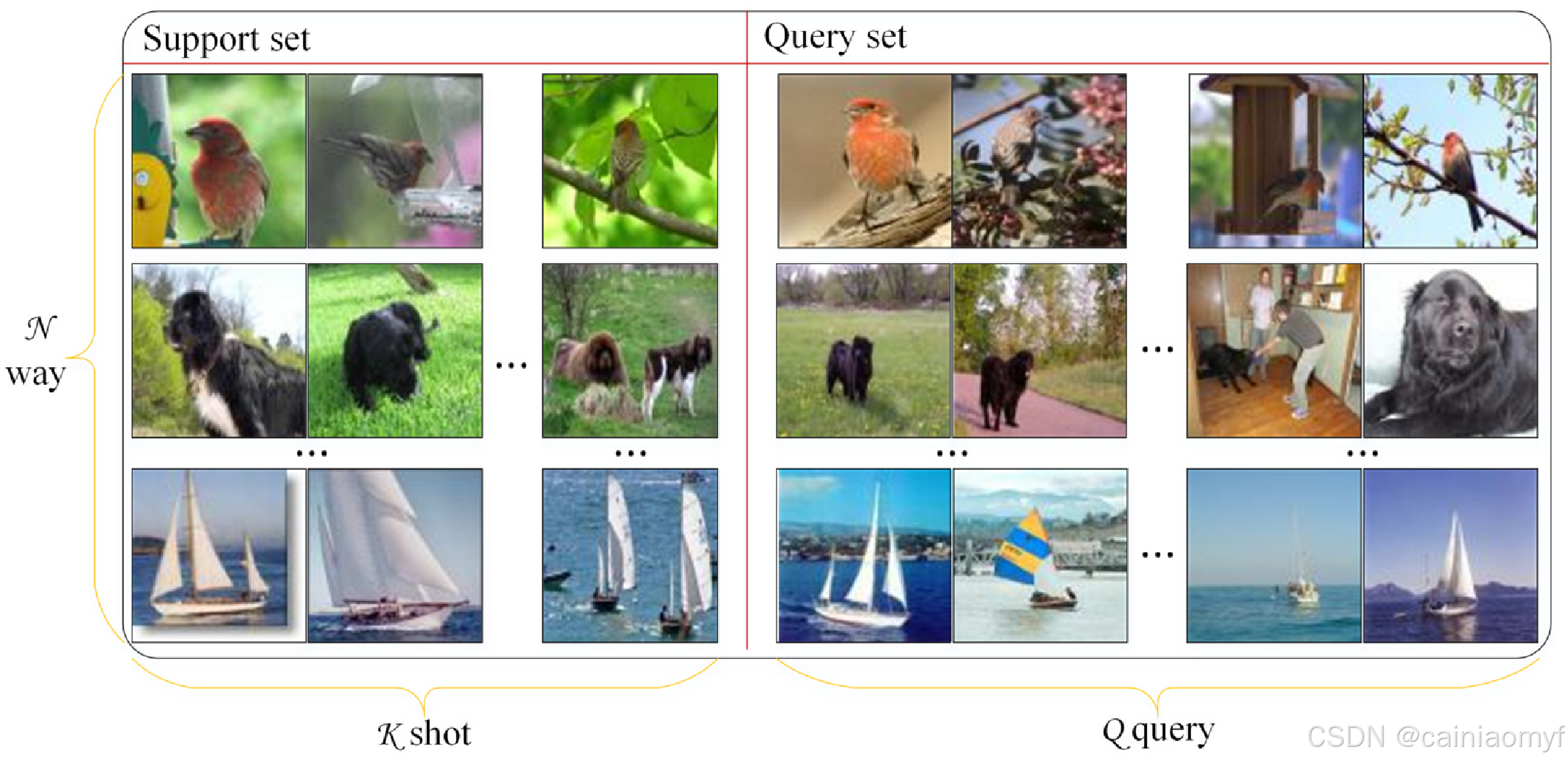
图1:回合/任务
T
\mathcal{T}
T的结构图。
采用了一种情境化的训练范式来实现小样本分类3。具体而言,从分布 P ( T ) \mathcal{P}(\mathcal{T}) P(T) 中采样情境/任务 T \mathcal{T} T,如图1所示。每个情境遵循传统的 N N N-way K K K-shot Q Q Q-query 格式,包含两个部分:支持集 S = { ( x i , y i ) } i = 1 N × K \mathcal{S} = \{(x_i, y_i)\}_{i=1}^{N \times K} S={(xi,yi)}i=1N×K 和查询集 Q = { ( x i , y i ) } i = 1 N × Q \mathcal{Q} = \{(x_i, y_i)\}_{i=1}^{N \times Q} Q={(xi,yi)}i=1N×Q,其中 S ∩ Q = ∅ \mathcal{S} \cap \mathcal{Q} = \emptyset S∩Q=∅。通常, N N N 设为 5, K K K 为 1 或 5, Q Q Q 为 15。支持集包含来自 D train / D test \mathcal{D}_{\text{train}} / \mathcal{D}_{\text{test}} Dtrain/Dtest 的 N N N 个类别中每个类别的 K K K 个样本。同样,查询集由这 N N N 个类别中的每个类别的 Q Q Q 个样本组成。
3.2. Overview
本研究提出了对比原型网络(CPN)来解决小样本分类问题。CPN的训练过程包含两个阶段:预训练阶段和元训练阶段。预训练过程相对简单,具体来说,编码器在训练数据集
D
train
\mathcal{D}_{\text{train}}
Dtrain 上以完全监督的方式通过交叉熵损失进行训练,类似于文献19。以miniImageNet数据集为例,网络在训练集中64个类别的样本上进行训练。训练完成后,将预训练模型的权重保存以用于元训练阶段。在预训练过程中生成的强嵌入特征为元训练阶段提供了重要支持。在元训练阶段,CPN主要由三个组件组成:伪原型(PP)、MixupPatch(MP)策略和对比学习方法。CPN基于原型网络进行改进。图2展示了CPN与原型网络(基准模型)之间的差异。如图所示,与基准模型相比,CPN包含两条互补路径:以原型网络为主任务,对比学习为辅助任务。在原型网络路径中,提出的PP策略使用查询样本的子集为每个类别生成伪原型,从而获得具有强表征能力的新类别原型。该方法解决了仅使用支持集样本构建的原型可能存在偏差的问题,无法充分表示预期的原型。为了进一步增强特征提取能力和模型的泛化性能,CPN引入了一条对比学习路径。在此路径中,首先利用提出的MP策略生成多样化的合成样本,然后进行对比学习。这使得模型能够聚焦于目标的最显著特征。这些改进使CPN在不同数据集上展现出强大的鲁棒性和优越的性能。图3详细展示了CPN的整体框架和方法,有助于更好地理解其工作原理和方法。这些算法在算法1、2和3中描述。

图 2. cpn 的简要结构以及基线和 cpn 之间的比较。

图 3. cpn 的详细结构。
CPN的决策过程包括以下步骤:
-
特征提取:将一个情境中的图像输入到深度卷积神经网络中,以提取高维特征表示。每张图像的特征被映射到嵌入空间,以便进行比较和分类。
-
生成伪原型:利用从支持集中获得的原型,通过距离测量对查询集中的样本进行分类,并基于概率值选择部分查询集样本生成伪原型。
-
获得新的强判别力原型:利用伪原型和初始原型,为每个类别生成具有更强判别性的新的原型。
-
分类决策:计算查询样本与每个类别的新原型之间的距离,将查询样本分配到对应于最近原型的类别以实现分类。
在元测试阶段,首先加载在元训练阶段训练的模型。该模型已学习如何将输入数据映射到嵌入空间,并将相似样本拉近,不同样本推远。随后,从 D test \mathcal{D}_{\text{test}} Dtest 中随机抽取若干情境,并使用该模型将 ( S , Q ) (\mathcal{S}, \mathcal{Q}) (S,Q) 中的样本映射到嵌入空间。基于 S \mathcal{S} S 中样本的特征计算每个类别的原型。最后,通过计算 Q \mathcal{Q} Q 中每个样本与各个原型的距离来预测其类别,如算法4所示。




3.3. Complementary path network structure
CPN利用由原型分类路径和对比学习路径组成的互补路径来训练网络。双路径使模型能够从不同的视角进行学习。原型网络路径计算类别中心,使模型能够从全局视角理解类别分布。相比之下,对比学习路径直接比较样本之间的相似性,从局部视角提供详细信息。原型网络和对比学习路径利用了不同类型的信息,能够相互补充。这种信息的互补使用帮助模型形成更全面的特征表示,从而增强了模型性能。
在原型分类路径中,首先使用 f θ f_{\theta} fθ 来获得 S \mathcal{S} S 中每个图像的嵌入表示。之后,使用公式 (1) 来确定每个类别的原型 P i \mathcal{P}_i Pi ( i = 1 , … , N i = 1, \dots, N i=1,…,N):
P i = 1 K ∑ k = 1 K f θ ( x s i , k ) (1) \mathcal{P}_i = \frac{1}{K} \sum_{k=1}^K f_{\theta}(x_{s_{i,k}}) \tag{1} Pi=K1k=1∑Kfθ(xsi,k)(1)
其中, f θ f_{\theta} fθ 表示特征嵌入函数/编码器, P i \mathcal{P}_i Pi 表示类别 i i i 的原型, x s i x_{s_{i}} xsi 表示支持集样本。
随后,使用编码器 f θ f_{\theta} fθ 对查询集图像进行编码,以获得查询集样本的嵌入向量表示。然后利用此嵌入表示与类别原型 P i \mathcal{P}_i Pi ( i = 1 , … , N i = 1, \dots, N i=1,…,N)计算相似性(如公式 (2)),以预测查询集样本的类别:
p i ( x q ) = p ( y = i ∣ x q ) = exp ( − μ ⋅ d ( f θ ( x q ) , P i ) ) ∑ j = 1 N exp ( − μ ⋅ d ( f θ ( x q ) , P j ) ) = exp ( − μ ⋅ ∥ f θ ( x q ) − P i ∥ 2 2 ) ∑ j = 1 N exp ( − μ ⋅ ∥ f θ ( x q ) − P j ∥ 2 2 ) (2) p_i(x_q) = p(y = i | x_q) = \frac{\exp(-\mu \cdot d(f_{\theta}(x_q), \mathcal{P}_i))}{\sum_{j=1}^N \exp(-\mu \cdot d(f_{\theta}(x_q), \mathcal{P}_j))} = \frac{\exp(-\mu \cdot \|f_{\theta}(x_q) - \mathcal{P}_i\|_2^2)}{\sum_{j=1}^N \exp(-\mu \cdot \|f_{\theta}(x_q) - \mathcal{P}_j\|_2^2)} \tag{2} pi(xq)=p(y=i∣xq)=∑j=1Nexp(−μ⋅d(fθ(xq),Pj))exp(−μ⋅d(fθ(xq),Pi))=∑j=1Nexp(−μ⋅∥fθ(xq)−Pj∥22)exp(−μ⋅∥fθ(xq)−Pi∥22)(2)
其中, p i ( x q ) p_i(x_q) pi(xq) 是 x q x_q xq 属于类别 i i i 的概率, d ( ⋅ , ⋅ ) d(\cdot, \cdot) d(⋅,⋅) 是距离度量,这里使用欧几里得距离, μ \mu μ 是一个标量。
最后,使用情境中所有查询样本的负对数概率作为分类损失(公式 (3))来更新网络参数:
L meta = − 1 ∣ Q ∣ ∑ x q ∈ Q log p ( x q ) (3) \mathcal{L}_{\text{meta}} = -\frac{1}{|\mathcal{Q}|} \sum_{x_q \in \mathcal{Q}} \log p(x_q) \tag{3} Lmeta=−∣Q∣1xq∈Q∑logp(xq)(3)
在支持集中样本数量有限的情况下,可能无法获得最佳类别原型,即得到的类别原型可能不是与所有相似样本距离最短的最佳原型。为解决此问题,我们提出了伪原型策略,以获得更具代表性的类别原型(第3.4节中介绍)。
对比学习具有多个优势。首先,它鼓励模型在特征空间中将相似样本拉近,同时将不同样本推远,使模型能够更准确地区分类别,尤其是在类别间存在细微差异时,从而显著增强模型的判别力。其次,对比学习方法相对简单且计算效率高。最后,在小样本学习场景中,对比学习能够通过有效提取和对比稀缺数据中的特征来充分利用有限样本,即使数据有限也能实现高效学习。因此,我们采用对比学习作为辅助路径以增强模型性能。此外,在对比学习路径中,我们提出了MixupPatch策略(第3.5节中介绍)。通过引入MixupPatch策略,对比学习可以利用增强的样本进行训练。该方法不仅增加了训练数据的多样性,还增强了模型在应对复杂和多变场景时的鲁棒性。
在起辅助作用的对比学习路径中,首先需要构建 ( Pos , Neg ) (\text{Pos}, \text{Neg}) (Pos,Neg)。本文中的 ( Pos , Neg ) (\text{Pos}, \text{Neg}) (Pos,Neg) 构建方式不同于传统对比学习方法。传统方法通常需要对每张图像进行两次随机数据增强。然而,基于FSL情境的特性3,我们首先计算每个情境中 N N N 个类别的原型,然后在每个类别的支持集中找到距离原型最近的样本,从而得到 N N N 个样本。这些 N N N 个样本用于为查询集构建正样本和负样本。具体而言,与查询样本属于同一类别的样本被视为正样本,而不属于同一类别的样本被视为负样本。如图2中的“构建 $(\text{Pos}, \text{Neg})”所示,紫色标记的圆圈代表查询样本,实紫色线指示的支持样本为正样本,虚黑线指示的支持样本为负样本。通过这种方式,对比学习路径可以与原型网络共享数据。然后使用相似度度量来测量两个样本嵌入之间的相似性。对比学习中常用的相似度度量为余弦相似度(公式 (4)):
sim ( v 1 , v 2 ) = v 1 ⋅ v 2 ∥ v 1 ∥ ∥ v 2 ∥ (4) \text{sim}(v_1, v_2) = \frac{v_1 \cdot v_2}{\|v_1\|\|v_2\|} \tag{4} sim(v1,v2)=∥v1∥∥v2∥v1⋅v2(4)
对比学习损失的计算
最后,计算对比学习损失。这样,同类样本在嵌入空间中更紧凑,而不同类样本则彼此远离,如图2的“嵌入空间”所示。对比学习利用噪声对比估计(NCE)函数来判断两个样本的嵌入是否相似20,如公式 (5):
L NCE = − log exp ( sim ( x q , x s + ) / τ ) exp ( sim ( x q , x s + ) / τ ) + exp ( sim ( x q , x s − ) / τ ) (5) \mathcal{L}_{\text{NCE}} = -\log \frac{\exp(\text{sim}(x_q, x_s^+)/\tau)}{\exp(\text{sim}(x_q, x_s^+)/\tau) + \exp(\text{sim}(x_q, x_s^-)/\tau)} \tag{5} LNCE=−logexp(sim(xq,xs+)/τ)+exp(sim(xq,xs−)/τ)exp(sim(xq,xs+)/τ)(5)
其中, x s + / x s − x_s^+/x_s^- xs+/xs− 为查询样本 x q x_q xq 的正样本/负样本, τ \tau τ 为温度系数。
由于基于情境构建的负样本数量较大,NCE不适用。因此,本研究使用NCE的变体InfoNCE21:
L InfoNCE = − log exp ( sim ( x q , x s + ) / τ ) exp ( sim ( x q , x s + ) / τ ) + ∑ x s − ∈ S exp ( sim ( x q , x s − ) / τ ) (6) \mathcal{L}_{\text{InfoNCE}} = -\log \frac{\exp(\text{sim}(x_q, x_s^+)/\tau)}{\exp(\text{sim}(x_q, x_s^+)/\tau) + \sum_{x_s^- \in \mathcal{S}} \exp(\text{sim}(x_q, x_s^-)/\tau)} \tag{6} LInfoNCE=−logexp(sim(xq,xs+)/τ)+∑xs−∈Sexp(sim(xq,xs−)/τ)exp(sim(xq,xs+)/τ)(6)
获得对比损失和元损失后,将它们结合生成混合损失。随后,嵌入模块 f θ f_{\theta} fθ 的参数 θ \theta θ 按公式 (7) 和 (8) 进行更新,其中 α \alpha α 为学习率:
L total = L meta + β L InfoNCE (7) \mathcal{L}_{\text{total}} = \mathcal{L}_{\text{meta}} + \beta \mathcal{L}_{\text{InfoNCE}} \tag{7} Ltotal=Lmeta+βLInfoNCE(7)
θ = θ − α ∇ θ L total (8) \theta = \theta - \alpha \nabla_{\theta} \mathcal{L}_{\text{total}} \tag{8} θ=θ−α∇θLtotal(8)
3.4. Pseudo-prototype strategy
仅使用支持集样本生成的类别原型(如原型网络PN)由于数据不足的困境,往往偏离预期原型,使得难以显著提升模型性能。基于FSL中的情境特征,我们知道查询集样本的类别必须与支持集样本的类别相同。因此,本研究提出伪原型策略,使用部分查询集样本生成伪原型,并将其与支持集样本生成的初始类别原型融合,以生成更准确的类别原型。新获得的原型与同类中的所有样本距离最近,而与其他类别中的所有样本距离最远。
如图3所示,首先使用公式 (1) 生成每个类别的初始原型。其次,使用公式 (2) 计算 N Q NQ NQ 个查询样本 x q x_q xq 属于每个类别的概率 p i ( x q ) p_i(x_q) pi(xq)( i = 1 , … , N i = 1, \dots, N i=1,…,N)。因此,每个查询样本 x q x_q xq 有 N N N 个概率值,表示该样本属于 N N N 个类别的可能性。如公式 (9) 所示,第一行表示每个类别的 Q Q Q 个查询集样本的索引, p i ( x q j ) p_i(x_{q_j}) pi(xqj) 表示第 j j j 个样本属于第 i i i 个类别的概率。对于第一个类别的查询样本, p 1 ( x q j ) p_1(x_{q_j}) p1(xqj)( j = 1 , … , Q j = 1, \dots, Q j=1,…,Q)的值一定高于其他类别的概率,依此类推。
p i ( x q j ) = p ( y = i ∣ x q j ) ( i = 1 , … , N ; j = 1 , … , Q ) (9) p_i(x_{q_j}) = p(y = i | x_{q_j}) \quad (i = 1, \dots, N; \, j = 1, \dots, Q) \tag{9} pi(xqj)=p(y=i∣xqj)(i=1,…,N;j=1,…,Q)(9)
首先,如图3的虚线箭头所示,对于每一类别的查询样本,根据概率值选择属于当前类别的前 H \mathcal{H} H 个样本。随后,利用这些 H \mathcal{H} H 个查询样本计算伪原型,如公式 (10) 所示。注意,这些 H \mathcal{H} H 个样本的特征并不是简单地取平均值,而是基于其概率进行加权求和,然后再进行平均操作。
查询样本的概率矩阵如下所示:
( 1 2 3 … Q p 1 ( x q 1 ) p 1 ( x q 2 ) p 1 ( x q 3 ) … p 1 ( x q Q ) p 2 ( x q 1 ) p 2 ( x q 2 ) p 2 ( x q 3 ) … p 2 ( x q Q ) ⋮ ⋮ ⋮ ⋱ ⋮ p N ( x q 1 ) p N ( x q 2 ) p N ( x q 3 ) … p N ( x q Q ) ) (9) \begin{pmatrix} 1 & 2 & 3 & \dots & Q \\ p_1(x_{q_1}) & p_1(x_{q_2}) & p_1(x_{q_3}) & \dots & p_1(x_{q_Q}) \\ p_2(x_{q_1}) & p_2(x_{q_2}) & p_2(x_{q_3}) & \dots & p_2(x_{q_Q}) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ p_N(x_{q_1}) & p_N(x_{q_2}) & p_N(x_{q_3}) & \dots & p_N(x_{q_Q}) \\ \end{pmatrix} \tag{9} 1p1(xq1)p2(xq1)⋮pN(xq1)2p1(xq2)p2(xq2)⋮pN(xq2)3p1(xq3)p2(xq3)⋮pN(xq3)………⋱…Qp1(xqQ)p2(xqQ)⋮pN(xqQ) (9)
伪原型的计算公式为:
P q i = 1 ∑ h = 1 H p i ( x q h ) ∑ h = 1 H f θ ( x q h ) ⋅ p i ( x q h ) (10) \mathcal{P}_q^i = \frac{1}{\sum_{h=1}^{\mathcal{H}} p_i(x_{q_h})} \sum_{h=1}^{\mathcal{H}} f_{\theta}(x_{q_h}) \cdot p_i(x_{q_h}) \tag{10} Pqi=∑h=1Hpi(xqh)1h=1∑Hfθ(xqh)⋅pi(xqh)(10)
其中, P q i \mathcal{P}_q^i Pqi 表示类别 i i i 的伪原型, x q h x_{q_h} xqh 表示第 h h h 个查询集样本, p i ( x q h ) p_i(x_{q_h}) pi(xqh) 表示第 h h h 个查询样本属于类别 i i i 的概率, f θ ( x q h ) f_{\theta}(x_{q_h}) fθ(xqh) 表示第 h h h 个查询样本的嵌入特征。
最后,通过公式 (11) 将初始原型和伪原型融合生成新的类别原型:
P i = λ P i + ( 1 − λ ) P q i (11) \mathcal{P}_i = \lambda \mathcal{P}_i + (1 - \lambda) \mathcal{P}_q^i \tag{11} Pi=λPi+(1−λ)Pqi(11)
3.5. MixupPatch strategy
深度神经网络(DNNs)在许多对人类而言困难的任务中展现了非凡的能力;然而,DNNs 依赖于大量的标记数据。因此,越来越多的策略被提出,以增加训练样本数量,解决标记样本不足的困境。常见的数据增强技术包括图像的颜色增强、缩放、裁剪、翻转和旋转。近年来,许多学者提出了不再增强整个图像的数据增强方法,而是以图像的某一部分为起点,通过修改该区域的图像或标签来实现数据增强。例如,mixup22 通过一定比例混合两个不同样本,Cutout23 随机将一些像素值设为0,而 Cutmix24 则结合了两者的特点,随机剪切和交换两个图像的部分矩形区域来合成新的图像。图4展示了这些方法之间的差异。

图4。各种数据增强方法的比较。
然而,上述方法仍然存在一些缺点。例如,mixup获得的样本局部上往往较为模糊且不自然,这容易使模型产生混淆。Cutout 会降低图像的利用率,因为一些像素被设为零或填充为随机噪声。尽管 Cutmix 生成的样本比 mixup 更具挑战性,有效提高了模型的泛化性能,但其实现对参数有较高的要求,若未正确选择参数,可能会产生负面效果。
因此,本文提出了mixupPatch策略,不仅在一定程度上避免了上述问题,还减轻了基础类别样本中数据偏差带来的影响。如图3和图4所示,首先,从一个情境的查询集中随机选择两个样本 x a x_a xa 和 x b x_b xb。然后,采用Cutmix的裁剪区域方法分别从这两张图像中裁剪出区域。裁剪区域表示为 R R R,而剩余区域表示为 R ′ R' R′。第三步,将 x a x_a xa 中的区域 R R R 与 x b x_b xb 中的区域 R R R 按一定比例混合,该部分的标签也按相同比例混合,而 R ′ R' R′ 部分的图像和标签保持不变(见公式 (12)-(15))。
x R a = κ x R a + ( 1 − κ ) x R b (12) x_R^a = \kappa x_R^a + (1 - \kappa)x_R^b \tag{12} xRa=κxRa+(1−κ)xRb(12)
y R a = κ y R a + ( 1 − κ ) y R b (13) y_R^a = \kappa y_R^a + (1 - \kappa)y_R^b \tag{13} yRa=κyRa+(1−κ)yRb(13)
x R ′ a = x R ′ a (14) x_{R'}^a = x_{R'}^a \tag{14} xR′a=xR′a(14)
y R ′ a = y a (15) y_{R'}^a = y_a \tag{15} yR′a=ya(15)
其中, x R a x_R^a xRa 和 x R b x_R^b xRb 分别表示 x a x_a xa 和 x b x_b xb 中的区域 R R R, y R a y_R^a yRa 和 y R b y_R^b yRb 分别表示 x a x_a xa 和 x b x_b xb 中区域 R R R 的标签。 κ \kappa κ 服从均匀分布 ( 0 , 1 ) (0, 1) (0,1)。
4. Experiments
4.1. Datasets
我们在5个数据集上进行实验。其中,miniImageNet、tieredImageNet 和 Fewshot CIFAR100 (FC100) 数据集用于标准的小样本图像分类,而 CUB200 和 Standard Cars (Cars) 数据集用于跨域小样本图像分类,如表2和图5所示。这些数据集具有很强的代表性,类别和样本数量相对较多,被广泛用于小样本学习研究,能够对 CPN 的可扩展性进行稳健评估。特别是,tieredImageNet、CUB200 和 Cars 数据集具有以下特点。tieredImageNet 以其大规模数据、复杂的层次结构和多种现实场景的覆盖而著称,因为这些图像来源于 ImageNet。CUB200 专注于鸟类物种,包含200类真实世界的鸟类照片,背景复杂多样,类别间视觉差异非常细微。Cars 数据集包含16,185张196种汽车类型的图像,涵盖了不同品牌、具体车型和年份。
-
miniImageNet: miniImageNet8 是 ILSVRC-201225 的子集,包含属于100个类别的60,000个样本,每个类别有600个样本。该数据集可作为 ImageNet 的替代品,用于模型验证、性能评估、小数据集训练等。一般而言,miniImageNet 的训练集、验证集和测试集分别包含64、16和20个类别。
-
tieredImageNet: tieredImageNet26 也是 ILSVRC-2012 的子集。tieredImageNet 包含779,165张属于34个大类的图像,可以进一步细分为608个类,每个大类包含10-30个类。tieredImageNet 考虑了 ImageNet 的层次结构,划分为20个大类(351个类)作为训练集,6个大类(97个类)作为验证集,以及8个大类(160个类)作为测试集。
-
FC100: FC10012 由100个类组成,每个类包含600张32x32的彩色图像。它源自 CIFAR-10027,包含100个类,每个类由600张32x32的彩色图像组成。FC100 依据大类而非具体类进行分类28。FC100 的训练集、验证集和测试集分别从20个大类(100个类)中创建。训练集包含12个大类(60个类),验证集包含4个大类(20个类),测试集包含4个大类(20个类)。
-
CUB200: CUB20029 是当前用于细粒度分类的基准数据集之一,包含来自200个类别的11,788张鸟类图像。每张图像提供类别和边界框等信息。该数据集划分为互不重叠的训练集、验证集和测试集,分别包含100、50和50个类别。
-
Cars: Cars 数据集30 包含来自196种不同品牌、年份和车型的车辆图像数据,共计16,185张图像。同样,该数据集划分为互不重叠的训练集、验证集和测试集,分别包含98、49和49个类别。
表2.本文使用的数据集
| Dataset | Apply | Class Number | Instances Number |
|---|---|---|---|
| miniImageNet | Train Val Test | 64 16 20 | 38400 9600 12000 |
| tieredImageNet | Train Val Test | 351(20) 97(6) 160(8) | 448695 124261 206209 |
| FC100 | Train Val Test | 60(12) 20(4) 20(4) | 36000 12000 12000 |
| CUB200 | Train Val Test | 100 50 50 | 5889 2942 2957 |
| Cars | Train Val Test | 98 49 49 | 8163 3993 4030 |
4.2. Research questions
为评估 CPN 的性能,我们关注以下研究问题:
- (RQ1) CPN 能否优于最先进的基准模型?
- (RQ2) CPN 在跨域场景中是否具有竞争力?
- (RQ3) CPN 中的哪个组件对分类的贡献更大?
- (RQ4) 选择的伪样本数量如何影响 CPN 的性能?
- (RQ5) λ \lambda λ 值对 CPN 性能有何影响?
4.3. Implementation details
实验中使用的网络主干为 ResNet-12。与文献19中的训练策略相似,我们首先进行100轮的预训练,并每10轮记录一次预训练权重。每轮的批量大小设为128。优化器使用带有0.9动量的随机梯度下降法(SGD),初始学习率为0.1,在第30轮和第60轮衰减20%。
在元训练阶段,使用欧几里得距离作为度量,并添加一个初始值为0.1的缩放系数。优化器仍然使用带有0.9动量的SGD,权重衰减为0.0005,初始学习率为0.0002。在mixupPatch策略中,混合系数 κ \kappa κ 服从均匀分布 ( 0 , 1 ) (0, 1) (0,1)。在伪原型策略中,选择的伪样本数量 H \mathcal{H} H 为8/9,融合新旧原型的融合系数 λ \lambda λ 为1/3或1/2。训练过程包括40轮,每轮由500个情境组成。报告的性能为10000个随机独立情境的平均准确率,置信区间为95%。
置信区间计算公式如下:
confidence
=
1.96
×
sta_deviation
×
epi_num
−
1
2
(16)
\text{confidence} = 1.96 \times \text{sta\_deviation} \times \text{epi\_num}^{- \frac{1}{2}} \tag{16}
confidence=1.96×sta_deviation×epi_num−21(16)
其中,
confidence
\text{confidence}
confidence 表示
epi_num
\text{epi\_num}
epi_num 测试任务上的标准差。
4.4. Comparison methods
为充分验证 CPN 的有效性,我们选择了多种具有竞争力的方法进行比较,包括基于优化的 MTL11;基于度量的 TADAM12 和 FEAT13,以及深度子空间网络-均值精化 (DSN-MR)14,Rethinking Few-Shot (RFS)31,Curvature Generation (CG)32,Meta-Navigator (Meta-NVG)33,使用重加权嵌入相似度的 Transformer 小样本分类 (FewTURE)34 和持续元学习算法 (CMLA)28。其中部分方法简述如下:
-
FEAT13: FEAT 是一种基于集合到集合函数的嵌入自适应方法,用于解决小样本学习问题。该方法通过学习自适应的嵌入函数,将少量样本数据转换为更鲁棒的表示,从而在小样本情况下实现分类任务。
-
CG32: CG 是一种在神经网络特征空间中生成曲率的方法,使得不同类别之间的泛化性和判别能力更强。通过引入曲率,模型可以学习更复杂的决策边界并捕捉数据的内在几何结构。
-
CMLA28: CMLA 是一种持续元学习算法。通过利用先前学习任务的知识和经验,模型在学习新任务时能够更快速地适应和迁移已有知识,从而提高机器学习的效率和泛化能力。
5. Result and discussion
5.1. Overall performance
我们在三个小样本数据集上针对RQ1进行了实验,如表3-5所示。
miniImageNet上的实验结果
实验结果如表3所示。CPN与最近的一些具有竞争力的方法进行了比较,包括 TADAM、MTL、ConstellationNet 和 DAM。如表所示,无论任务形式是1-shot还是5-shot,CPN都产生了最佳结果。对于1-shot和5-shot,CPN的准确率分别为67.30%和82.19%。通过观察各方法在1-shot和5-shot上的性能,可以发现5-shot的性能总是优于1-shot,其原因在于5-shot提供了更多的支持样本。
当主干网络为 ResNet-12 时,CPN的性能在1-shot和5-shot上分别比基于度量的 TADAM 高出8.8%和5.49%。这种性能提升当然离不开伪原型的贡献,伪原型参与了原型的校准过程,使得新原型更接近预期原型。相比基于优化的 MTL,CPN的性能分别高出6.1%和6.69%,这是因为带有对比学习的 CPN 学习到了更好的嵌入特征,并增强了特征提取器的能力。
此外,在1-shot任务中,CPN的性能分别比 ConstellationNet、CMM、DSN-MR 和 DAM 高出2.41%、7.57%、2.7% 和6.91%;在5-shot任务中,CPN的性能分别比 ConstellationNet、CMM、DSN-MR 和 DAM 高出2.24%、10.12%、2.68% 和8.35%。从表3中也可以明显看出,CPN的性能优于使用更深层网络的方法。例如,在1-shot和5-shot任务中,CPN的准确率均高于 Simple Siamese (SimSiam) 和带有均匀性正则化的 SimSiam (UniSiam)。
| Method | Backbone | miniImageNet 1-shot | miniImageNet 5-shot |
|---|---|---|---|
| DSN-MR ([14]) | ResNet-12 | 64.60 ± 0.72 | 79.51 ± 0.50 |
| TADAM ([12]) | ResNet-12 | 58.50 ± 0.30 | 76.70 ± 0.30 |
| ConstellationNet([36]) | ResNet-12 | 64.89 ± 0.23 | 79.95 ± 0.17 |
| Adaptive Meta-Transfer (A-MET) ([37]) | ResNet-12 | 64.61 ± 0.47 | 80.06 ± 0.32 |
| Multi-task learning ([38]) | ResNet-12 | 59.84 ± 0.22 | 77.72 ± 0.09 |
| FEAT ([13]) | ResNet-12 | 66.78 ± 0.20 | 82.05 ± 0.14 |
| Complex Metric Module (CMM)([39]) | ResNet-12 | 59.73 | 72.07 |
| Learn to Forget (L2F) ([40]) | ResNet-12 | 59.71 ± 0.49 | 77.04 ± 0.42 |
| MTL ([11]) | ResNet-12 | 61.20 ± 1.80 | 75.50 ± 0.80 |
| Deep Attentive Metric (DAM) ([41]) | ResNet-12 | 60.39 ± 0.21 | 73.84 ± 0.16 |
| SimSiam † ([42]) | ResNet-18 | 62.80 ± 0.37 | 79.85 ± 0.27 |
| UniSiam ([35]) | ResNet-18 | 63.26 ± 0.36 | 81.13 ± 0.26 |
| CPN (Ours) | ResNet-12 | 67.30 ± 0.30 | 82.19 ± 0.40 |
tieredImageNet上的实验结果
同样地,CPN在tieredImageNet上优于其他方法,如表4所示。CPN在1-shot和5-shot情境中的准确率分别达到了74.2%和85.63%。
在1-shot情境中,CPN分别比RFS、DSN-MR、CMM和DAM高出4.46%、6.81%、15.67%和10.11%。在5-shot情境中,CPN分别比RFS、DSN-MR、CMM和DAM提高了1.22%、2.78%、11.78%和7.24%。
与miniImageNet数据集相比,CPN在tieredImageNet数据集上的准确率更高,训练时间也相应增加。这可能是由于tieredImageNet数据集包含更多的样本。
| Method | Backbone | tieredImageNet 1-shot | tieredImageNet 5-shot |
|---|---|---|---|
| FEAT ([13]) | ResNet-12 | 70.80 ± 0.23 | 84.79 ± 0.16 |
| RFS ([31]) | ResNet-12 | 69.74 ± 0.72 | 84.41 ± 0.55 |
| CG ([32]) | ResNet-12 | 71.66 ± 0.23 | 85.50 ± 0.15 |
| DSN-MR ([14]) | ResNet-12 | 67.39 ± 0.82 | 82.85 ± 0.56 |
| Multi-task learning ([38]) | ResNet-12 | 67.11 ± 0.12 | 83.69 ± 0.02 |
| CMM ([39]) | ResNet-12 | 58.53 | 73.85 |
| L2F ([40]) | ResNet-12 | 64.04 ± 0.48 | 81.13 ± 0.39 |
| A-MET ([37]) | ResNet-12 | 69.39 ± 0.57 | 81.11 ± 0.39 |
| DAM ([41]) | ResNet-12 | 64.09 ± 0.23 | 78.39 ± 0.18 |
| UniSiam ([35]) | ResNet-18 | 65.18 ± 0.39 | 82.28 ± 0.29 |
| SimSiam† ([42]) | ResNet-18 | 64.05 ± 0.40 | 81.40 ± 0.30 |
| CPN (Ours) | ResNet-12 | 74.20 ± 0.20 | 85.63 ± 0.30 |
FC100上的实验结果
表5显示了CPN与其他方法在FC100上的准确率。如所示,CPN实现了最佳分类性能。CPN所使用的主干网络为ResNet-12。与同样使用ResNet-12作为主干的TADAM、MTL、Meta-NVG、FewTURE和L2F相比,CPN在1-shot情境中的分类准确率分别高出9.96%、4.96%、3.66%、2.38%和8.17%。即使CMLA和LGCMLA采用了更深的主干网络,CPN的性能仍优于它们。
由于FC100数据集的图像分辨率较低,相较于前两个数据集,FC100上的准确率不如其他数据集,但其训练时间显著较短。与其他方法相比,基于度量的方法以其高效性著称。由于CPN是一种基于度量的方法,并在基准PN上进行了改进,我们在算法复杂性方面对CPN和PN进行了比较。
从复杂性来看,PN作为基准方法,其计算复杂性主要集中在每个类别原型的计算 O ( N K ) O(NK) O(NK) 和每个查询样本与原型的距离计算 O ( N Q ) O(N\mathcal{Q}) O(NQ)。在许多实际情况下,支持样本数量 K K K 和查询样本数量 Q Q Q 为常数,因此复杂性可以进一步简化为 O ( N ) O(N) O(N),其中 N N N 是类别数。相比之下,CPN的计算复杂性并不高,如算法2和3的伪代码所示。CPN的计算复杂性主要来源于以下部分:伪原型生成、MixupPatch数据增强和对比学习路径。
在伪原型生成过程中,计算每个类别的初始原型的复杂性为
O
(
N
K
)
O(NK)
O(NK),将每个查询样本与每个类别原型进行比较的复杂性为
O
(
N
Q
)
O(N\mathcal{Q})
O(NQ),选择和更新伪原型的复杂性为
O
(
N
Q
log
Q
+
N
H
)
O(N\mathcal{Q}\log\mathcal{Q} + N\mathcal{H})
O(NQlogQ+NH)。在MixupPatch数据增强过程中,通过增强查询样本生成新样本,这部分复杂性可以忽略。在对比学习路径中,将每个查询样本与每个类别原型进行比较的复杂性为
O
(
N
Q
)
O(N\mathcal{Q})
O(NQ)。因此,CPN的总复杂性为
O
(
N
K
+
2
N
Q
+
N
Q
log
Q
+
N
H
)
O(NK + 2N\mathcal{Q} + N\mathcal{Q}\log\mathcal{Q} + N\mathcal{H})
O(NK+2NQ+NQlogQ+NH)。由于选择的样本数量
H
\mathcal{H}
H 为常数,复杂性可以进一步简化为
O
(
N
)
O(N)
O(N)。这表明,随着类别数的增加,CPN的计算需求呈线性增长,在相对低的计算复杂度下实现了高计算效率和更好的性能,详见图6。

图6。训练每个数据集所需的时间。
| Method | CUB200 1-shot | CUB200 5-shot | Cars 1-shot | Cars 5-shot |
|---|---|---|---|---|
| MNet ([46]) | 35.89 ± 0.51 | 51.37 ± 0.77 | 30.77 ± 0.47 | 38.99 ± 0.64 |
| MNet+FT ([46]) | 36.61 ± 0.53 | 55.23 ± 0.83 | 29.82 ± 0.44 | 41.24 ± 0.65 |
| RelationNet ([46]) | 42.44 ± 0.77 | 57.77 ± 0.69 | 29.11 ± 0.60 | 37.33 ± 0.68 |
| RelationNet+FT ([46]) | 44.07 ± 0.77 | 59.46 ± 0.71 | 28.63 ± 0.59 | 39.91 ± 0.69 |
| RelationNet+LRP ([47]) | 41.57 ± 0.40 | 57.70 ± 0.40 | 30.48 ± 0.30 | 41.21 ± 0.40 |
| RelationNet+ATA ([48]) | 43.02 ± 0.40 | 59.36 ± 0.40 | 31.79 ± 0.30 | 42.95 ± 0.40 |
| GNN ([46]) | 45.69 ± 0.68 | 62.25 ± 0.65 | 31.79 ± 0.51 | 44.28 ± 0.63 |
| GNN+FT ([46]) | 47.47 ± 0.75 | 66.98 ± 0.68 | 31.61 ± 0.53 | 44.90 ± 0.64 |
| GNN+LRP ([47]) | 43.89 ± 0.50 | 62.86 ± 0.50 | 31.46 ± 0.40 | 46.07 ± 0.40 |
| GNN+ATA ([48]) | 45.00 ± 0.50 | 66.22 ± 0.50 | 33.61 ± 0.40 | 49.14 ± 0.40 |
| Baseline (PN) | 45.16 ± 0.10 | 62.48 ± 0.15 | 33.04 ± 0.10 | 46.81 ± 0.05 |
| CPN | 47.58 ± 0.20 | 63.45 ± 0.30 | 34.58 ± 0.20 | 47.14 ± 0.15 |
5.2. Cross-domain few-shot classification
为回答RQ2,我们使用了两个细粒度数据集进行跨域研究。模型首先在 miniImageNet 训练集上进行训练,并在验证集上选择效果最佳的模型参数。然后,在 CUB200 和 Cars 测试集上评估模型的泛化能力。这两个数据集上的模型性能如表6所示。
与第5.1节中的结果类似,在 CUB200 和 Cars 数据集上,5-shot 的性能始终优于 1-shot,表明增加支持样本在跨域情况下也能对模型产生积极影响。然而,相对于第5.1节中的单域数据集性能,CPN 在跨域情境中的性能有所下降,因为跨域情境更加具有挑战性。此外,相比于对 CUB200 的泛化性能,CPN 在迁移至 Cars 数据集时的表现更差。这是因为 CUB200 与 miniImageNet 相似,而 Cars 与 miniImageNet 的差异更为明显。
在表6中,1-shot 情境下,CPN 在两个数据集上均优于现有方法。然而,在 5-shot 情境中,其分类准确率不及图神经网络 (GNN)+FT(FT 表示特征转换层固定)和 GNN+ATA(对抗任务增强)。尽管如此,GNN+FT 涉及一个包含图神经网络和特征转换的复杂模型,可能需要更长的训练时间和更多的计算资源。此外,选择合适的超参数对于 GNN+FT 至关重要,错误的选择可能显著降低模型性能。GNN+ATA 除了需要大量资源和调参外,还面临模型过度关注对抗特征的风险。然而,提出的 CPN 在资源需求和调参需求方面更加宽容。
与基准方法 PN3 相比,CPN 的分类准确率更高。在 1-shot 设置下,CPN 在 CUB200 和 Cars 数据集上的准确率分别比基准方法高出 2.42% 和 1.54%。
5.3. Ablation study
为回答RQ3,通过消融实验研究了CPN中三个不同组件对各数据集分类准确率的影响。CPN的三个关键组件为:对比学习(CL)、mixupPatch(MP)和伪原型(PP)。表7展示了测试这三个组件的结果。可以看出,每个组件对分类准确率的提升都有不同程度的贡献,且当三个组件组合时提升效果最大。通过比较(1)和(4)的结果可以发现,当将CPN应用于三个数据集时,分类准确率显著提升,尤其是在1-shot情境下。这是因为与5-shot相比,1-shot在计算初始原型时样本更少,添加伪原型后得到的新类别原型更接近预期原型。
对比学习的消融分析
表7展示了在miniImageNet、tieredImageNet和FC100上5-way 1/5-shot情境下的消融实验结果。通过比较(1)和(2)可以看出,对比学习对分类准确率的提升有积极影响。例如,在1-shot情境下,使用对比学习的准确率在miniImageNet上提升了1.74%,在tieredImageNet上提升了2.24%,在FC100上提升了1.54%,表明添加对比损失后的混合损失更有利于模型学习到良好的嵌入。在图7-8中也可以看到对比学习对每个数据集的准确率提升效果。基准准确率趋势用青色线表示,而加入对比学习后的准确率趋势用黄色线表示。显然,加入对比学习后准确率有效提高,提升速度更快,使用时间更短。
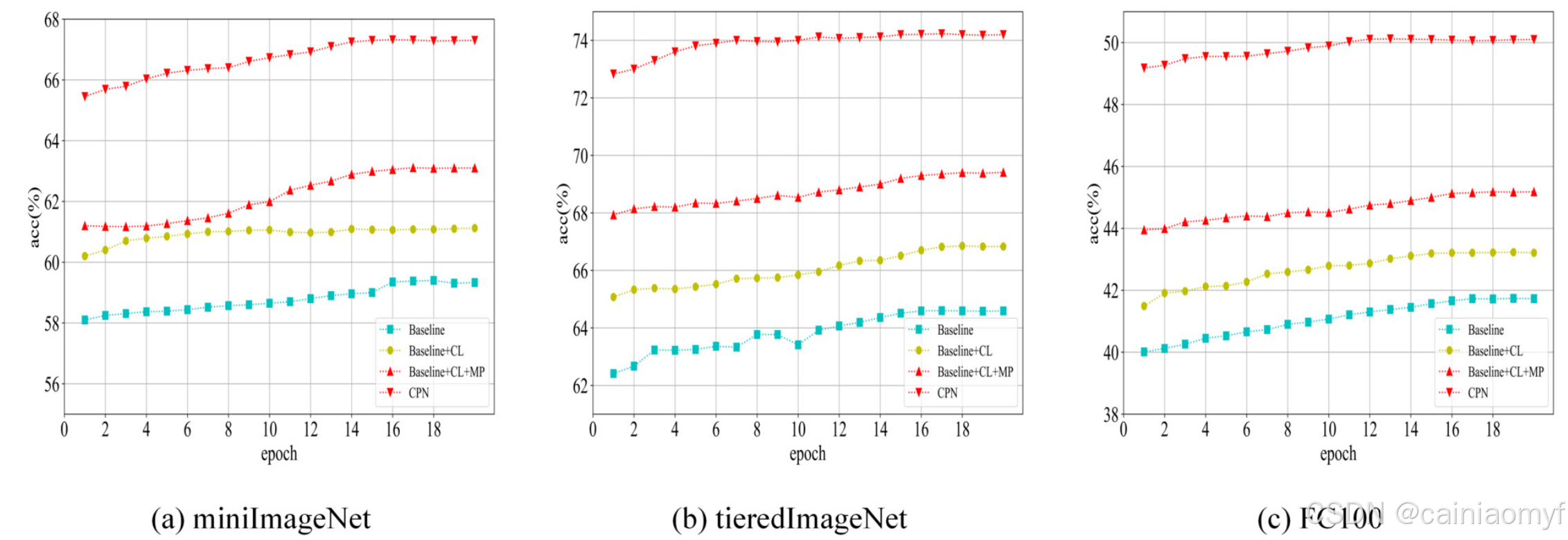
图 7. 5 way 1 shot设置下消融

图 8. 5 way 5 shot设置下消融。
mixupPatch的消融分析
表7中(2)和(3)的结果差异反映了mixupPatch对分类的影响。mixupPatch在三个数据集上的1/5-shot情境中显示出显著的提升,特别是在1-shot情境下,tieredImageNet数据集的准确率提高了2.58%。这是因为mixupPatch的加入不仅增加了样本多样性,还增强了模型的定位和泛化能力,消除了基础类别带来的归纳偏差,并引导模型关注目标最具区分性的部分。此外,我们将mixupPatch与CutMix进行了比较,结果如表8所示。尽管mixupPatch和CutMix均提升了分类准确率,但mixupPatch的提升幅度明显更大。例如,在1-shot情境下,mixupPatch在三个数据集上的精度分别比CutMix高出0.94%、1.34%和0.98%。这可能是因为CutMix直接混合了两个样本的标签,引入了较高的标签噪声,使得学习过程更加复杂。
表8:mixuppatch和cutmix效果的比较。
| Method | miniImageNet (1-shot) | miniImageNet (5-shot) | tieredImageNet (1-shot) | tieredImageNet (5-shot) | FC100 (1-shot) | FC100 (5-shot) |
|---|---|---|---|---|---|---|
| CutMix | 62.15 | 79.35 | 68.07 | 82.66 | 44.15 | 62.91 |
| MixupPatch | 63.09 | 79.90 | 69.41 | 83.40 | 45.13 | 63.20 |
伪原型的消融分析
通过表7中(3)和(4)的结果比较,在1-shot情境下,伪原型策略使miniImageNet数据集的分类性能提升了4.21%,使tieredImageNet数据集的准确率提升了4.79%,伪原型策略利用部分查询集样本生成伪原型。由于该策略以另一种方式扩展了支持集,伪原型衍生出的类别原型比初始类别原型更接近预期类别原型。
表 7 消融研究每个组件的效果。基线:原型网络; cl:对比学习模块; mp:mixuppatch 模块;pp:伪原型模块('⋆':with;'-':没有)。

5.4. H \mathcal{H} H的影响
为回答RQ4,我们进一步实验了不同的 H \mathcal{H} H值。由于每个情境中每类的查询集样本数量为15,我们将 H \mathcal{H} H设置在0到15的范围内,观察到当 H \mathcal{H} H为15时,CPN的性能最佳。
如图9所示,在5-way 1/5-shot条件下,当 H \mathcal{H} H小于8/9时,随着样本数量 H \mathcal{H} H的增加,准确率提高。这是因为该策略在一定程度上缓解了数据不足的问题。随后,准确率保持稳定。然而,随着 H \mathcal{H} H进一步增加,准确率开始下降,因为用于计算伪原型的低置信度查询集样本的真实标签与支持集样本的标签不同。

图 9. 伪样本数量的影响
5.5. λ \lambda λ的影响
为回答RQ5,对在混合原型和伪原型时使用的 λ \lambda λ值进行了实验,以选择最优的 λ \lambda λ值。
表 9 λ \lambda λ对分类精度的影响。
| Method | miniImageNet (1-shot) | miniImageNet (5-shot) | tieredImageNet (1-shot) | tieredImageNet (5-shot) | FC100 (1-shot) | FC100 (5-shot) |
|---|---|---|---|---|---|---|
| λ \lambda λ= 1/3 | 67.30 ± 0.30 | 81.95 ± 0.10 | 74.20 ± 0.20 | 84.07 ± 0.30 | 50.06 ± 0.40 | 65.10 ± 0.30 |
| λ \lambda λ= 1/2 | 66.96 ± 0.40 | 82.19 ± 0.40 | 73.16 ± 0.50 | 85.63 ± 0.30 | 49.10 ± 0.30 | 65.74 ± 0.10 |
| λ \lambda λ= 2/3 | 65.10 ± 0.50 | 81.71 ± 0.11 | 71.25 ± 0.40 | 84.49 ± 0.50 | 47.39 ± 0.50 | 65.46 ± 0.20 |
| λ \lambda λ= 1 | 63.09 ± 0.20 | 79.90 ± 0.15 | 69.41 ± 0.48 | 83.40 ± 0.15 | 45.13 ± 0.56 | 63.20 ± 0.10 |
如表9和图10所示,在1-shot情境下,当 λ \lambda λ为1/3时,三个数据集上的准确率最高。在5-shot情境下,当 λ \lambda λ为1/2时,三个数据集上的准确率最高。因为在1-shot情境中,每个类别的支持集中仅有一个样本,支持集获得的初始类别原型与预期原型的距离较远。加入伪原型后,预期原型更加偏向伪原型;因此,初始类别原型的比例相对较小。而在5-shot情境中,每个类别的支持集样本更多,导致初始类别原型与预期原型的差距缩小,因此 λ \lambda λ的值相应增加。

图10.
λ
\lambda
λ值的影响
5.6. Feature visualization
在小样本学习中,t-分布随机邻域嵌入 (t-SNE)35 是一种常用的降维和可视化技术,用于理解高维特征的分布。为了进一步验证 CPN 的有效性,我们使用 t-SNE 进行可视化。首先从 miniImageNet 的测试集中提取一个情境,然后分别使用基准模型和 CPN 模型获取图像特征,并进行 t-SNE 可视化。图11-12展示了三个数据集上的可视化结果,其中每个点代表样本的特征嵌入,不同颜色的点代表来自不同类别的样本。第一行表示样本的数据分布,第二行和第三行分别表示基准模型和 CPN 的可视化结果。
通过检查类别间的分离和类内紧密度,可以评估模型在区分类别内外样本上的有效性。如图所示,与基准模型相比,CPN 展现了以下两个特性:
- 清晰的类别边界和较大的类别间距:不同类别形成了具有清晰边界的独立聚类,不同类别的聚类之间距离显著。这表明 CPN 成功学习到了每个类别的判别特征。
- 紧密的类内聚类:来自同一类别的样本紧密聚集在一起,形成紧密的分组。这表明 CPN 有效捕捉到了同一类别样本之间的内在相似性。
然而,CPN 也存在一定的局限性。例如,我们观察到一些可能代表具有挑战性的样本或数据集噪声的异常点。
此外,我们使用梯度加权类激活映射 (Grad-CAM)36 来进一步研究 CPN 的有效性。Grad-CAM 生成类激活图,显示模型关注的图像区域。这不仅有助于理解模型的决策过程,还可以验证特征表示的有效性。如果模型关注的区域与目标对象的关键特征对齐,这表明模型已经学习到了有效的特征表示。此外,Grad-CAM 可以帮助识别并解决噪声或背景干扰等异常情况。
首先,我们从 miniImageNet 中随机选择了5张图像,并将基准模型和 CPN 模型学习到的特征输入到 Grad-CAM 中,以显示它们在进行预测时关注的输入图像区域。如图13所示,第二列为原始图像,第一列和第三列分别表示基准模型和 CPN 模型关注的图像区域。
结果表明,与基准模型相比,CPN 一致地关注对象最相关的部分。例如,在狮子、斑马和柠檬的图像中,基准模型的注意力较窄,而 CPN 的关注范围更全面,覆盖了对象的关键部分。这表明 CPN 在识别和聚焦对象的关键部分方面表现更好,这有助于其在分类任务中的性能提升。
6. Theoretical and practical implications
本研究提出了一种新的小样本学习方法——CPN。通过结合伪原型策略、MixupPatch策略和对比学习方法,该方法有效地解决了小样本学习中数据稀缺和泛化性能差的问题。从理论上讲,所提出的方法不仅在特征提取和模型泛化方面具有显著优势,还为小样本学习提供了新的解决方案。伪原型策略利用部分查询样本为每个类别生成伪原型,从而获得具有更强表征能力的新类别原型,解决了仅使用支持集样本构建原型时产生的偏差问题。MixupPatch策略通过生成多样化的合成样本缓解了数据不足的问题。对比学习方法进一步优化了特征提取能力,使模型能够更好地聚焦目标的显著特征。对 miniImageNet、tieredImageNet、FC100、CUB200 和 Cars 等多个常用小样本学习数据集的实验验证了 CPN 的有效性和鲁棒性,为该领域的进一步研究奠定了基础。
所提出的 CPN 在实践中具有重要意义,特别是在解决数据稀缺和类别不平衡问题方面。MixupPatch策略可以生成多样化的合成样本,有效应对现实应用中数据集不平衡的问题,从而提升模型的鲁棒性和适应性。多数据集上的实验结果表明,CPN 在图像分类任务中表现优异,显示出其在实时图像识别和分类应用中的潜力。例如,在医学诊断中,获取大规模标记数据往往困难且成本高昂。CPN 可以在有限标记数据的情况下提供更准确的诊断结果,从而提高诊断的准确性和效率。在智能驾驶系统中,必须在各种复杂场景下识别和分类对象。通过增强特征提取和泛化能力,CPN 能够更好地在复杂场景中识别和分类对象,从而提高智能驾驶系统的安全性和可靠性。这些应用前景不仅展示了 CPN 的实际价值,也为未来的研究和开发提供了广阔的可能性。
7. Conclusion and future work
本研究提出了使用 CPN 来实现小样本分类,包含三个重要组件:互补路径网络结构、伪原型策略和 mixupPatch 策略。互补路径网络结构利用混合损失提供更准确的梯度信息来训练优化模型;伪原型通过使用查询集生成伪原型,使得计算的类别原型更接近预期的类别原型;MixupPatch 通过按比例混合两个样本的图像和标签,在一定程度上缓解了数据不足的问题。在五个小样本分类基准数据集上的大量实验中,CPN 被证明在性能上具有竞争力。
尽管 CPN 展现了令人印象深刻的性能,但它仍然存在一定的局限性。与 FEAT 相比,CPN 的特征自适应能力较弱。FEAT 利用基于 Transformer 的自适应嵌入方法,可以根据任务需求实时调整特征表示,使来自不同类别的样本更好地分离。相比之下,CPN 的特征表示适应性较弱,依赖对比学习任务和伪原型策略,无法像 FEAT 那样根据任务需求实时调整特征表示。
在跨域泛化能力方面,尽管 CPN 在单域小样本学习中表现良好,但其跨域泛化能力有限。在跨域小样本学习任务中,尤其当源域和目标域之间差异较大时,CPN 的性能下降。通过比较第 5.1 节和第 5.2 节的准确率,可以发现后者的分类准确率远低于前者。这是因为 CPN 的原型和特征表示在训练过程中过度依赖源域的数据分布,导致模型在遇到目标域样本时难以有效适应新的分布。
综上所述,CPN 对不同数据分布的适应性尚需进一步提升,这促使我们在训练模型时进一步探讨以下问题:如果前后任务属于完全不同的类别,模型应如何表现?因此,下一步将探讨是否可以实现小样本学习的连续性。
J. Liu, W. Huang, H. Li, et al., Slafusion: attention fusion based on sax and lstm for dangerous driving behavior detection, Inf. Sci. 640 (2023) 119063. ↩︎ ↩︎
F. Erivaldo, G.G. Yen, Pruning of generative adversarial neural networks for medical imaging diagnostics with evolution strategy, Inf. Sci. 558 (2021) 91–102. ↩︎
J. Snell, K. Swersky, R. Zemel, Prototypical networks for few-shot learning, in: NIPS, 2017, pp. 4077–4087. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
X. Chen, X. Zheng, K. Sun, W. Liu, Y. Zhang, Self-supervised vision transformer-based few-shot learning for facial expression recognition, Inf. Sci. 634 (2023) 206–226. ↩︎
S. Gidaris, N. Komodakis, Dynamic few-shot visual learning without forgetting, in: CVPR, 2018, pp. 4367–4375. ↩︎ ↩︎
Z. Chen, Y. Fu, Y. Wang, L. Ma, W. Liu, M. Hebert, Image deformation meta-networks for one-shot learning, in: CVPR, 2019, pp. 8680–8689. ↩︎ ↩︎
R. Zhang, T. Che, Z. Ghahramani, Y. Bengio, Y. Song, Metagan: an adversarial approach to few-shot learning, in: NeurIPS, 2018, pp. 2371–2380. ↩︎ ↩︎
O. Vinyals, C. Blundell, et al., Matching networks for one shot learning, in: NIPS, 2016, pp. 3630–3638. ↩︎ ↩︎ ↩︎ ↩︎
F. Sung, Y. Yang, et al., Learning to compare: relation network for few-shot learning, in: CVPR, 2018, pp. 1199–1208. ↩︎ ↩︎ ↩︎ ↩︎
C. Finn, P. Abbeel, S. Levine, Model-agnostic meta-learning for fast adaptation of deep networks, in: ICML, vol. 70, 2017, pp. 1126–1135. ↩︎ ↩︎ ↩︎
Q. Sun, Y. Liu, T. Chua, B. Schiele, Meta-transfer learning for few-shot learning, in: CVPR, 2019, pp. 403–412. ↩︎ ↩︎ ↩︎
B.N. Oreshkin, P. Rodriguez, A. Lacoste, Tadam: task dependent adaptive metric for improved few-shot learning, in: NeurIPS, 2018, pp. 719–729. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
H. Ye, D. Hu, H. Zhan, F. Sha, Few-shot learning via embedding adaptation with set-to-set functions, in: CVPR, 2020, pp. 8808–8817. ↩︎ ↩︎ ↩︎
C. Simon, P. Koniusz, R. Nock, M. Harandi, Adaptive subspaces for few-shot learning, in: CVPR, 2020, pp. 4136–4145. ↩︎ ↩︎
K. He, H. Fan, Y. Wu, et al., Momentum contrast for unsupervised visual representation learning, in: CVPR, 2020, pp. 9726–9735. ↩︎ ↩︎ ↩︎
T. Chen, S. Kornblith, et al., A simple framework for contrastive learning of visual representations, in: ICML, vol. 119, 2020, pp. 1597–1607. ↩︎ ↩︎
B. Mao, X. Zhang, L. Wang, Q. Zhang, S. Xiang, P. C., Learning from the target: dual prototype network for few shot semantic segmentation, Proc. AAAI Conf. Artif. Intell. 36 (2) (2022) 1953–1961. ↩︎ ↩︎
J. Jia, X. Feng, H. Yu, Few-shot classification via efficient meta-learning with hybrid optimization, Eng. Appl. Artif. Intell. 127 (2024) 107296. ↩︎
H. Huang, J. Zhang, J. Zhang, Q. Wu, C. Xu, Ptn: a Poisson transfer network for semi-supervised few-shot learning, Proc. AAAI Conf. Artif. Intell. 35 (2) (2021) 1602–1609. ↩︎ ↩︎
M. Gutmann, A. Hyvärinen, Noise-contrastive estimation: a new estimation principle for unnormalized statistical models, in: AISTATS, vol. 9, 2010, pp. 297–304. ↩︎
A.v.d. Oord, Y. Li, O. Vinyals, Representation learning with contrastive predictive coding, 2018. ↩︎
H. Zhang, M. Cisse, Y.N. Dauphin, D. Lopez-Paz, mixup: beyond empirical risk minimization, in: ICLR, 2018. ↩︎
T. DeVries, G.W. Taylor, Improved regularization of convolutional neural networks with cutout, 2017. ↩︎
S. Yun, D. Han, S.J. Oh, S. Chun, J. Choe, Y. Yoo, Cutmix: regularization strategy to train strong classifiers with localizable features, in: ICCV, 2019, pp. 6022–6031. ↩︎
O. Russakovsky, J. Deng, et al., Imagenet large scale visual recognition challenge, Int. J. Comput. Vis. 115 (3) (2015) 211–252. ↩︎
M. Ren, E. Triantafillou, et al., Meta-learning for semi-supervised few-shot classification, in: ICLR, 2018. ↩︎
A. Krizhevsky, G. Hinton, Learning multiple layers of features from tiny images, Technical report, 2009. ↩︎
M. Jiang, F. Li, L. Liu, Continual meta-learning algorithm, Appl. Intell. 52 (4) (2022) 4527–4542. ↩︎ ↩︎ ↩︎
C. Wah, S. Branson, P. Welinder, P. Perona, S. Belongie, The caltech-ucsd birds-200-2011 dataset, California Institute of Technology, 2011, Tech. Rep. CNS-TR-2011-001. ↩︎
J. Krause, M. Stark, et al., 3d object representations for fine-grained categorization, in: ICCV, 2013, pp. 554–561. ↩︎
Y. Tian, Y. Wang, Rethinking few-shot image classification: a good embedding is all you need?, in: ECCV, vol. 12359, 2020, pp. 266–282. ↩︎
Z. Gao, Y. Wu, Y. Jia, M. Harandi, Curvature generation in curved spaces for few-shot learning, in: ICCV, 2021, pp. 8671–8680. ↩︎ ↩︎
C. Zhang, H. Ding, G. Lin, R. Li, C. Wang, C. Shen, Meta navigator: search for a good adaptation policy for few-shot learning, in: ICCV, 2021, pp. 9415–9424. ↩︎
M. Hiller, M. Ma, M. Harandi, T. Drummond, Rethinking generalization in few-shot classification, NeurIPS (2022). ↩︎
M.L. der Van, G.E. Hinton, Visualizing data using t-sne, J. Mach. Learn. Res. (2008) 2579–2605. ↩︎
R.R. Selvaraju, M. Cogswell, et al., Grad-cam: visual explanations from deep networks via gradient-based localization, in: ICCV, 2017, pp. 618–626. ↩︎
























 3605
3605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








