下面的答案仅供参考!
1. 试把以下程序划分为基本块并作出其程序流图。
read C
A:=0
B:=1
L1: A:=A+B
if B≥C goto L2
B:=B+1
goto L1
L2: write A
halt
解题思路:要画出程序的控制流程图,先得将程序划分成基本块的形式。基本块的划分分为3个步骤:
第1步:满足下列3个条件中任一个的语句可充当入口。
1)程序的第一个语句。
2)能由条件转移语句或无条件转移语句转移到的语句。
3)紧跟在条件转移语句后面的语句。
第2步:根据第1步求出的每一入口语句,构造其所属的基本块。
1)由该人口语句到另一入口语句(不包括该入口语句)之间组成的语句序列,或
2)由该入口语句到-转移语句(包括该转移语句)之间组成的语句序列,或
3)由该入口语句到一停语句(包括该停语句)之间组成的语句序列。
第3步:凡未被纳入某一基本块中的语句,都是程序中控制流程无法到达的语句,从而也是不会被执行的语句,可把它们从程序中删除。
解答
根据第1个步骤,程序中的入口有程序的第1个语句(read(C)),转移语句能转移到的有2个语句(其语句标号分别为L1、L2),以及条件语句(标号为L1)之后的语句(B:=B+1)。总共找出4个入口。因此,程序至少可分为4个基本块。
根据第2个步骤有:由第1个入口(程序的第1个语句)到下一入口语句(标号为L1的转移语句,不包括该入口语句)之间组成的语句序列为第1个基本块;第2入口语句到if B≥C goto L2为第二个基本块;第3个入口到一转移语句(goto L1,包括该转移语句)之间组成的语句序列为第3个基本块;第4个入口到停语句(包括该转移语句)为第4个基本块。
第2步做完后,程序中不存在控制流程无法到达的语句,因此不需要进行语句的删除操作。基本块划分好之后,可根据基本块间执行的可能顺序构造出基本块间的有向边,从而得到程序的流图。
因此,程序共分为4个基本块(B1到B4),以及相应的程序流图如图所示(一个方框代表一个基本块)。

2. 试把以下程序划分为基本块并作出其程序流图。
read A, B
F:=1
C:=A*A
D:=B*B
if C<D goto L1
E:=A*A
F:=F+1
E:=E+F
write E
halt
L1: E:=B*B
F:=F+2
E:=E+F
write E
if E>100 goto L2
halt
L2: F:=F-1
goto L1
答:
根据第1个步骤,程序中的入口有程序的第1个语句(read(A,B)),转移语句能转移到的有2个语句(其语句标号分别为L1、L2),以及2个条件语句(if C<D goto L1)之后的语句(E:=A*A到halt),(if E>100 goto L2)之后的语句(halt)。总共找出5个入口。因此,程序至少可分为5个基本块。
根据第2个步骤有:由第1个入口(程序的第1个语句)到下一入口语句(第二个基本块,不包括该入口语句)之间组成的语句序列为第1个基本块;第2入口语句E:=A*A到halt为第2个基本块;第3个入口到一转移语句(if E>100 goto L2,包括该转移语句)之间组成的语句序列为第3个基本块;if E>100 goto L2之后的halt为第4个基本块。L2到转移语句(goto L1)为第5个基本块。
第2步做完后,程序中不存在控制流程无法到达的语句,因此不需要进行语句的删除操作。基本块划分好之后,可根据基本块间执行的可能顺序构造出基本块间的有向边,从而得到程序的流图。
该程序可划分为5个基本块:B1、B2、B3、B4和B5。
其程序流图如下图所示。


3. 试对以下基本块B1和B2:
B1: A:=B*C B2: B:=3
D:=B/C D:=A+C
E:=A+D E:=A*C
F:=2*E G:=B*F
G:=B*C H:=A+C
H:=G*G I:=A*C
F:=H*G J:=H+I
L:=F K:=B*5
M:=L L:=K+J
M:=L
分别应用DAG对它们进行优化,并就以下两种情况分别写出优化后的四元式序列:
(1)假设只有G、L、M在基本块后面还要被引用;
(2)假设只有L在基本块后面还要被引用。
【解答】(1)基本块B1的DAG构造。

根据构造基本块的DAG的算法,处理每一个四元式后构造出的DAG如图中各子图所示(其步骤从略)。图(a),(b),…,(i)分别对应于四元式①,②,…,⑨。


现在写出基本块B1优化后的四元式序列。
若只有G,L,M在基本块B1后仍要引用,则优化后的四元式序列为
G:=B*C
H=G*G
L:=H*G
M:=L
或者

若只有L在基本块后面还要被引用,则优化后的四元式序列为
G:=B*C
H=G*G
L:=G*H
或者
S1 :=B*C
S2 :=S1*S1
L:=S2*S1
(S1、S2为临时变量)
(2)B2的DAG构造过程
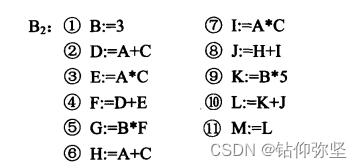
处理每一个四元式后构造出的DAG如图中各子图所示(步骤从略)。图(a),(b) , …,(k)分别对应于四元式①,②,…,


若只有G、L、M在基本块后还要被引用,在优化后的四元式序列为:
现在写出基本块B优化后的四元式序列。
L,M,G在B2后仍要被引用,则优化后的四元式序列为:
D:=A+C
E:=A*C
F:=D+E
G:=3*F
L:=F+15
M:=L
若只有L在基本块后还要被引用,则优化后的四元式序列为:
D:=A+C
E:=A*C
F:=D +E
L:= 15 + F
或者
S1:=A+C
S2:=A*C
S3:=S1+S2
L:= 15+S3
(s1、s2、S3为临时变量)
4. 对以下四元式程序,对其中循环进行循环优化。
I: =1
read J, K
L: A:=K*I
B:=J*I
C:=A*B
write C
I:=I+1
if I<100 goto L
halt
解题思路:先进行基本块划分,再画程序的流图。由于要进行循环优化,于是可考虑代码外提、强度削弱和删除归纳变量等优化方法。
答:先将程序划分为基本块:B1,B2和B3。其程序流图如下图所示。从流图中可知要优化的循环是指基本块B2。

对循环B2中的代码分别实行代码外提、强度削弱和删除归纳变量优化如下:
(1)代码外提:由于循环中没有不变运算,故此项先不做。
(2)强度削弱:由于循环中有
A : =K*Ⅰ
B:=J*Ⅰ
其中K,J在循环中值不发生改变,Ⅰ每次增加10。而程序每循环一次,A的值增加一个常量(K* 10),B的值增加一个常量(J* 10)。因此对A,B的赋值运算可进行强度削弱,即可将表达式中的乘法运算(*)改为加法运算(+)。同时,增加两个四元式用于计算两个常量(K*10)和(J* 10).强度削弱后的程序流图如下图所示。

(3)删除基本归纳变量:循环中Ⅰ是基本归纳变量,A,B是与Ⅰ同族的归纳变量,且有如下线性关系:
A:=K*Ⅰ
B:=J*Ⅰ
于是,条件I<100完全可用A<100*K或B<100*J替代。这样基本块B2中的控制条件和控制语句便可改写为:
T1:= 100 * K
if A <T1 goto L'
或改写为:
T2:= 100 * J
if B<T2 goto L'
于是程序流图就变为如下图所示的情形。

变换循环控制条件
控制条件经过以上改变后,就可删除基本块B2中的语句I: =I+1。又语句T1:=100*K是循环中的不变运算,可从基本块B2中外提到基本块B1中,于是程序流图最后变为如图所示的形式。
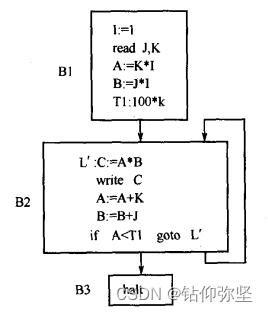
删除归纳变量及代码外提
5. 以下程序是某程序的最内循环,是对它进行循环优化。
A:=0
I:=1
L1: B:=J+1
C:=B+I
A:=C+A
if I=100 goto L2
I:=I+1
goto L1
L2:
答:程序的流图如下图所示。流图中有一条回边B3→B2,且 B2 DOM B3,所以有一个循环{B2,B3},B2是循环入口结点,也是出口结点。现对循环{B2,B3}进行优化。

(1)代码外提。对于B2中的赋值四元式B: =J+1,由于循环中没有对J的定值操作,所有对J的定值都在循环外,所以它是循环的不变运算,可以进行代码外提,提到循外进行计算。
(2)删除归纳变量。循环中Ⅰ是基本归纳变量,C是与Ⅰ同族的归纳变量,且两者有如下的线性关系:
C:= B+Ⅰ
于是,条件Ⅰ= 100完全可以用C=B+100替代,相应的I:=I+1可用C:=C+1替代。再将新出现的不变运算提到循环外。优化后的程序流图如下图所示。

6. 试写出以下程序段
for i:=1 to M do
for j:=1 to N do
A[i,j]:=B[i,j]
的四元式中间代码,然后求出其中的循环,并进行循环优化。
以下答案来源于网络,仅供参考。
答:中间代码如下,用三地址代码表示:
i:=1
j:=1
L1: if i<=M goto L2
L2: if j<=N goto L3
L3: t1 := i * N t1 := t1+j
t2 := A-N t2 := t2-1
t3 := t2[t1] t4 := i * N
t4 := t4+j t5 := B-N
t5 := t5-1 t6 := t5[t4]
t3:=t6
i:=i+1
j:=j+1
goto L1

代码外提:

强度削弱

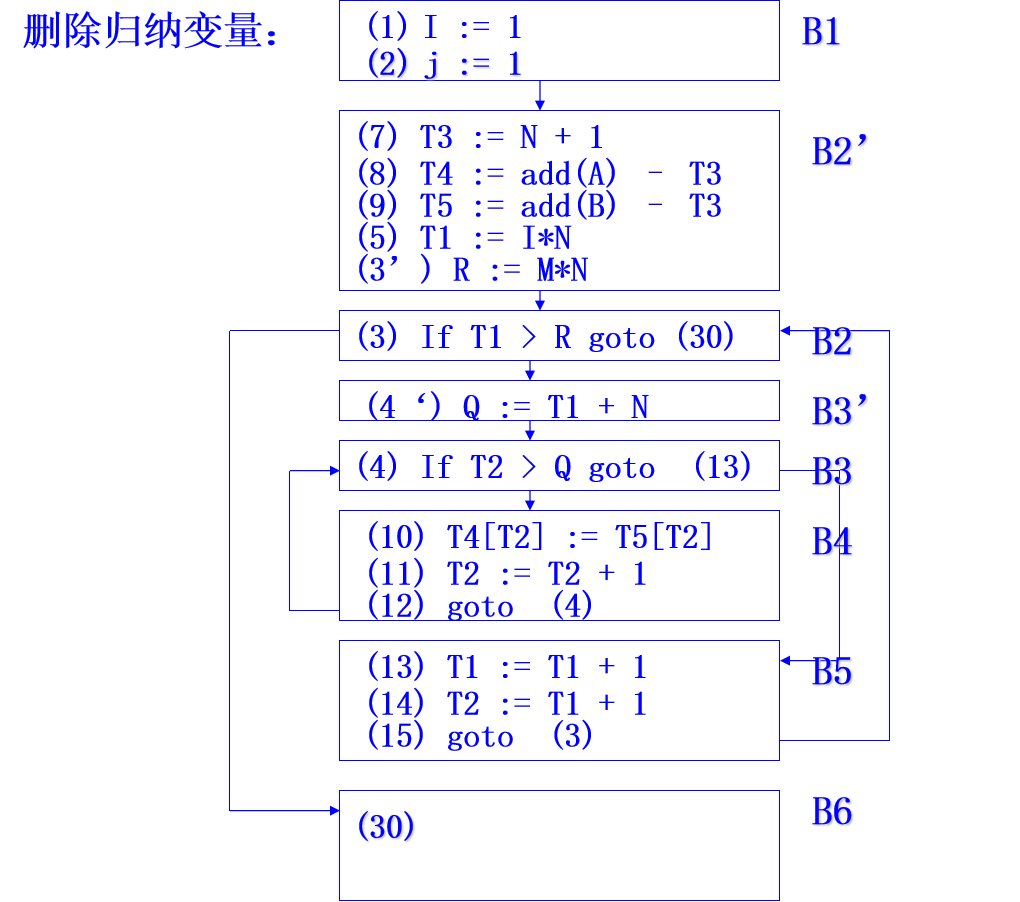
删除归纳变量

另一个版本:
强度消弱(1):
给一个相似的例子,可以参考
写出以下程序段
的四元式序列(假定按字编址,并且数组每个元素占一个机器字,A,B是按静态分配的N×N矩阵,地址计算时C值已知),请给出程序流图,并进行循环优化。
把四元式划分基本块后,得到结果如下图所示。
其中B1,B2,B3,B4,B5,B6,B7分别代表基本块。由此,我们可以作出如下图所示的流图。
由上图可知,B5→B4,B6→B2为二条回边,故有循环:{B4,B5}和{B2,B3,B4,B5,B6}。通过对循环进行代码外提、强度削弱、删除归纳变量等优化工作得到如下图所示的优化后的程序流图(其中B2’,B4'是代码外提时建立的前置结点):
如果在循环优化时进一步用DAG方式对基本块进行优化,可得如下四元式代码序列:
7. 下面是应用筛法求2到N之间素数个数的程序:
begin
read N;
for i:=2 to N do
A[i]:=true;/*置初值*/
for i:=2 to N** 0.5 do /*运算符**代表乘方*/
if A[i] then /* i是一个素数*/
begin
for j:=2*i to N by i do
A[j]:=false /*j可被i除尽*/
end;
COUNT:=0;
for i:=2 to N do
if A[i] then COUNT:=COUNT+1;
print COUNT
end
(1) 试写出其四元式中间代码,假设对数组A用静态分配分配存储单元;
答:采用字节地址,两个字节作为一个机器字。
(1)程序的四元式中间代码如下:
B1: read N /* 置初值 */
i := 2
B2: if i > N goto B4 /* 第一个for语句 */
B3: T1 := i
T2 := addr(A) /* 数组A的基地址 */
T1 := 2 * T1
T2[T1] := true
i := i + 1
goto B2
B4: i := 2
T3 := N ** 0.5
T3 := [T3] + 1 /* [T3]是对T3的值取整 */
B5: if i > T3 goto B12
B6: T4 := i
T5 := addr(A)
T4:= 2 * T4
if T5[T4] goto B8
B7: goto B11
B8: j := 2 * i
B9: if j > N goto B11 /* 第三个for语句 */
B10: T6 := j
T7 := addr(A)
T6 := 2 * T6
T7[T6] = false
j := j + i
goto B9
B11: i := i + 1
goto B5
B12:
(2) 作出流图并求其中的循环;
根据四元式的中间代码,可划分成基本块B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11。其程序流图如下:
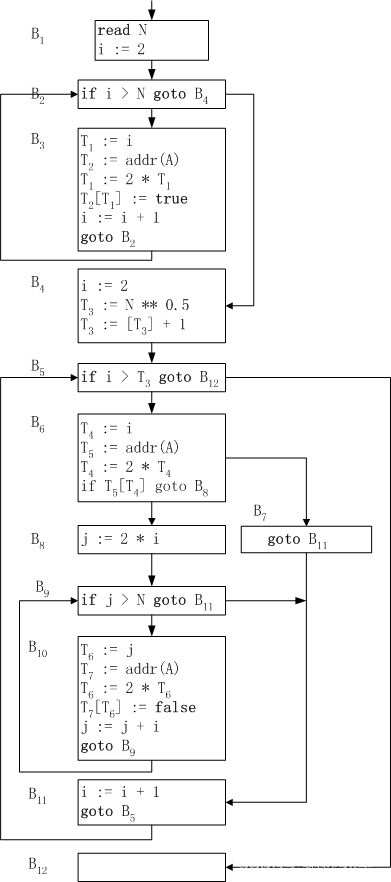
考察上面的程序流图:
D(B3) = { B1, B2, B3 } 又有 B3 -> B2,因此 B3 -> B2 是一条回边。根据它找到的循环 L1 = { B2, B3 }。
D(B10) = { B1, B2, B4, B5, B6, B9, B10 },又有 B10 -> B9,所以 B10 -> B9 是一条回边。根据这条回边找到循环 L2 = { B9, B10 }。
D(B11) = { B1, B2, B4, B5, B6, B9, B11 },又有 B11 -> B5,因此 B11 -> B5 是一条回边。根据这条回边找到循环 L3 = { B11, B9, B10, B8, B7, B6, B5 }
(3) 进行代码外提;
把在循环中不随循环变化的操作提到循环外的前置结点中,且在基本块中作复写传播和删除无用赋值。结果程序流图如下:
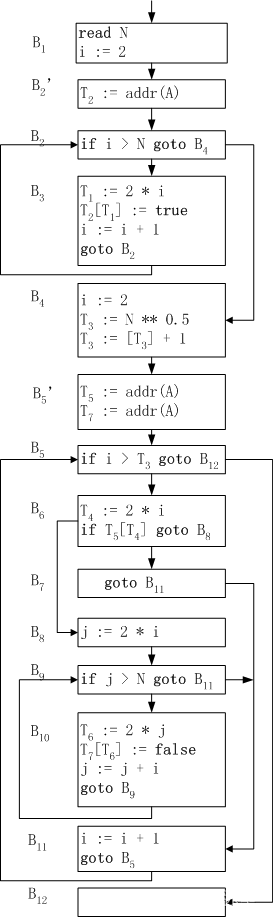
(4) 进行强度削弱和删除归纳变量。
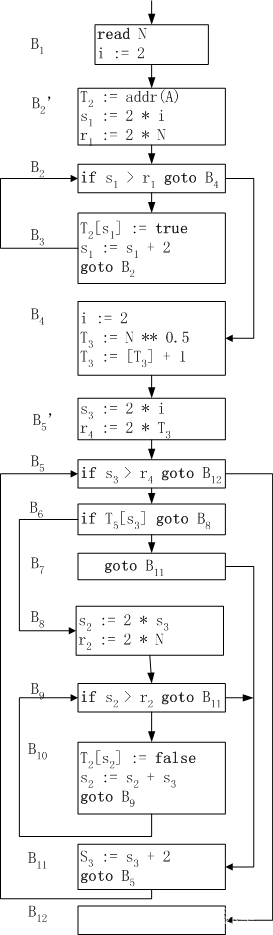
进行强度削弱和删除归纳变量后,其程序流图如下:








 文章介绍了如何将程序划分为基本块并构建程序流图,针对给定的程序实例进行了基本块的划分和程序流图的绘制。同时,文章详细探讨了程序的优化,包括代码外提、强度削弱和删除归纳变量等循环优化技术,并给出了具体的应用示例。
文章介绍了如何将程序划分为基本块并构建程序流图,针对给定的程序实例进行了基本块的划分和程序流图的绘制。同时,文章详细探讨了程序的优化,包括代码外提、强度削弱和删除归纳变量等循环优化技术,并给出了具体的应用示例。






























 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










