强化学习07——时序差分方法

本篇博客内容源于课程《强化学习的数学原理》 赵世钰老师 西湖大学，旨在记录学习强化学习的过程。

TD算法

TD算法的思想

和MC算法一样，TD算法是一类无模型算法，TD算法在数学上干了一件什么事情呢？即求解给定策略的贝尔曼方程(Policy evaluation),它是一种在线的（Online）算法，可以立刻用得到的信息更新数据，因此可以解决一些Continuing tasks。

回到状态值函数state value的定义$$v_{\pi }(s)=\mathbb{E}[R+\gamma G|S=s],s\in \mathcal{S}$$其中$G$是折扣回报，我们有$$\mathbb{E}[G|S=s]=\sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })=\mathbb{E}[v_{\pi }(S^{\prime })|S=s]$$其中$S^{\prime }$是下一时刻的状态，因此引出贝尔曼方程的另一种形式，即贝尔曼期望方程：$$v_{\pi }(s)=\mathbb{E}[R+\gamma v_{\pi }(S^{\prime })|S=s],s\in \mathcal{S}.$$同样反映的是不同状态的state value的关系。我们可以通过Robbins-Monro算法求解该方程。
定义$g(v(s))$：$$g(v(s))=v(s)-\mathbb{E}[R+\gamma v_{\pi }(S^{\prime })|s]$$故求解上述贝尔曼转化为如下问题：$$g(v(s))=0.$$对应噪音观测：$$\begin{array}{rl}\tilde{g}(v(s))& =v(s)-\left[\begin{array}{c}r+\gamma v_{\pi }(s^{\prime })\end{array}\right]\\ & \begin{array}{rl}& =\underset{g(v(s))}{\underbrace{\left(v(s)-\mathbb{E}[R+\gamma v_{\pi }(S^{\prime })|s]\right)}}+\underset{\eta }{\underbrace{\left(\mathbb{E}[R+\gamma v_{\pi }(S^{\prime })|s]-[r+\gamma v_{\pi }(s^{\prime })]\right)}}.\end{array}\end{array}$$
$r,s^{\prime }$是$R,S^{\prime }$的样本。因此利用Robbins-Monro算法求解$g(v(s))=0$有$$\begin{array}{rl}{v}_{k+1}(s)& \begin{array}{r}=v_k(s)-{\alpha }_k\tilde{g}(v_k(s))\end{array}\\ & =v_k(s)-{\alpha }_k(v_k(s)-[r_k+\gamma v_{\pi }(s_k^{\prime })\left]\right),k=1,2,3,\dots \end{array}$$其中$v_k(s)$是对$v_{\pi }(s)$的第k次估计，$r_k,s_k^{\prime }$是$R,S^{\prime }$的第k次采样。但有两个问题我们需要解决：

1. 我们需要样本数据$\{(s,r,s^{\prime })\}$
   解决办法：可以使用一个episode的序列样本$\{(s_t,r_{t+1},s_{t+1})\}$。
2. 尚不明确$v_{\pi }(s_k)$
   解决办法：使用$v_k(s_k^{\prime })$代替$v_{\pi }(s_k)$（用一个样本或一次估计代替真实值）
   有了这些分析，接下来正式引入TD算法。

TD算法

算法需要的数据：由给定策略$\pi$生成的序列$\{(s_t,r_{t+1},s_{t+1})\}$
TD算法如下：
$$v_{t+1}(s_t)=v_t(s_t)-{\alpha }_t(s_t)\left[v_t(s_t)-[r_{t+1}+\gamma v_t(s_{t+1})]\right],$$
$$v_{t+1}(s)=v_t(s),\forall s\ne s_t,$$
其中$t=0,1,2,\dots$ , $v_t(s_t)$是 $v_{\pi }(s_t)$的估计；${\alpha }_t(s_t)$ 是 $s_t$ 关于 $t$ 的学习率。第二个式子表示只更新$t$时刻访问到的状态。
TD算法注释如下：
$$\underset{\text{new estimate}}{\underbrace{v_{t+1}(s_t)}}=\underset{\text{current estimate}}{\underbrace{v_t(s_t)}}-{\alpha }_t(s_t)[\stackrel{\text{TD error }{\delta }_t}{\overbrace{v_t(s_t)-[\underset{\text{TD target }{\bar{v}}_t}{\underbrace{r_{t+1}+\gamma v_t(s_{t+1})}}]}}],$$
随着更新$v_t(s_t)\to {\bar{v}}_t$,相应的$v_t(s_t)\to 0$。

TD算法的收敛性

注意Remark第二点，条件：$$\sum _t{\alpha }_t(s)=\infty \text{ and }\sum _t{\alpha }_t^2(s)<\infty$$要求每个状态$s$被访问的次数要足够多。

Sarsa算法

上一小节介绍的TD算法能对给定策略进行评估，但强化学习的最终目的是要找到最优策略，马上要介绍的Sarsa算法能直接对动作值函数action values进行评估，并给出最优策略，简单来讲Sarsa算法就是action values版本的TD算法。

假定我们有经验序列（experience）：$\{(s_t,r_{t+1},s_{t+1}){\}}_t$
Sarsa算法如下：
$$\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma q_t(s_{t+1},a_{t+1})]],\\ q_{t+1}(s,a)& =q_t(s,a),\forall (s,a)\ne (s_t,a_t),\end{array}$$
其中$q_t(s_t,a_t)$是$q_{\pi }(s_t,a_t)$的一次估计，学习率${\alpha }_t(s_t,a_t)$依赖于$s_t,a_t$。而实际上Sarsa算法求解的就是关于动作值函数的贝尔曼期望方程$$q_{\pi }(s,a)=\mathbb{E}\left[R+\gamma q_{\pi }(S^{\prime },A^{\prime })|s,a\right],\forall s,a.$$

n-step Sarsa算法

我们知道可以如下分解：
$$\begin{array}{rl}{q}_{\pi }(s,a)& =\mathbb{E}\left[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|s,a\right],\forall s,a.\\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{q}_{\pi }(S_{t+2},A_{t+2})|s,a\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{q}_{\pi }(S_{t+3},A_{t+3})|s,a\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^n{q}_{\pi }(S_{t+n},A_{t+n})|s,a\right]\\ & =\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|s,a\right]\end{array}$$
而实际上n-step Sarsa算法求解的就是关于贝尔曼期望方程：
$$q_{\pi }(s,a)=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^n{q}_{\pi }(S_{t+n},A_{t+n})|s,a\right]$$
自然需要经验序列：$\{(s_t,a_t,r_{t+1},s_{t+1},a_{t+1},\dots ,r_{t+n},s_{t+n},a_{t+n})\}$
n-step Sarsa算法如下：$$\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)\\ & -{\alpha }_t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma r_{t+2}+\cdots +{\gamma }^n{q}_t(s_{t+n},a_{t+n})]].\end{array}$$

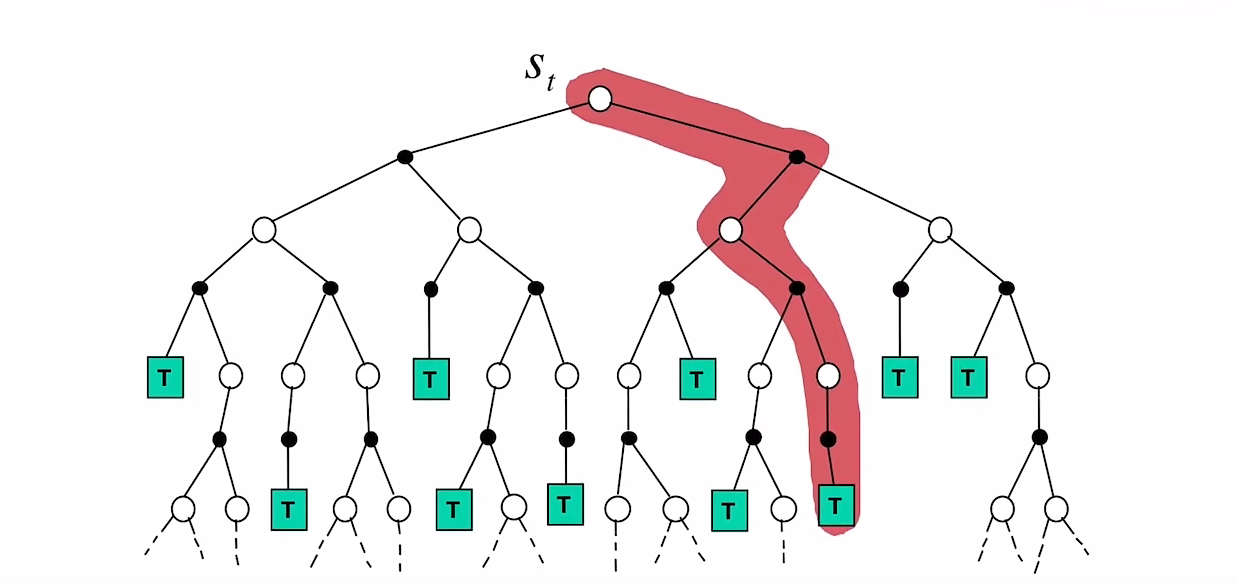
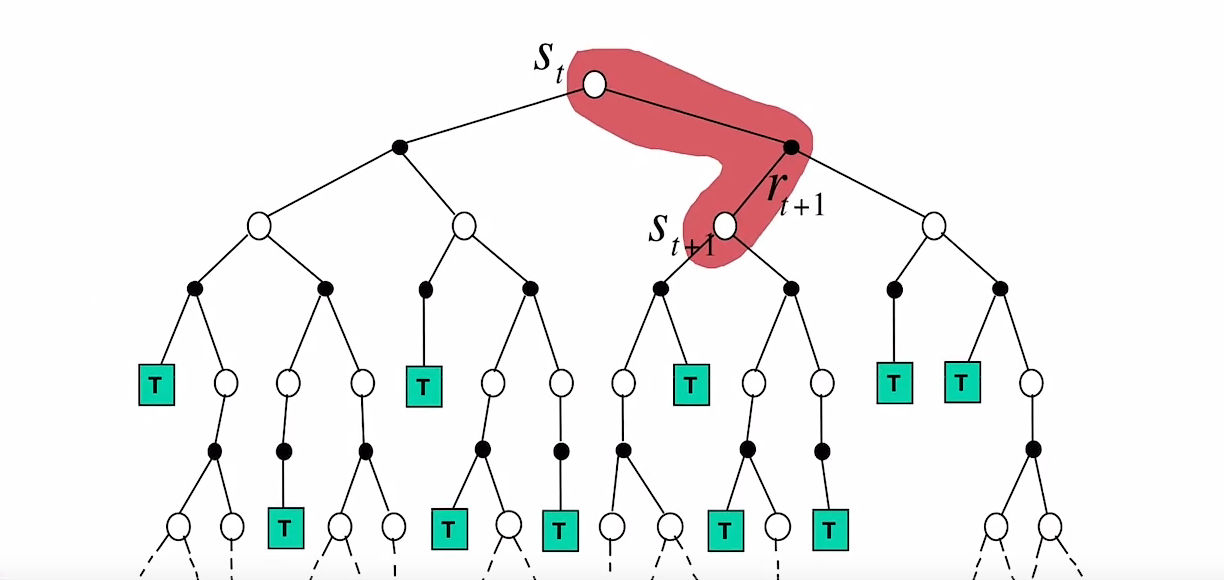
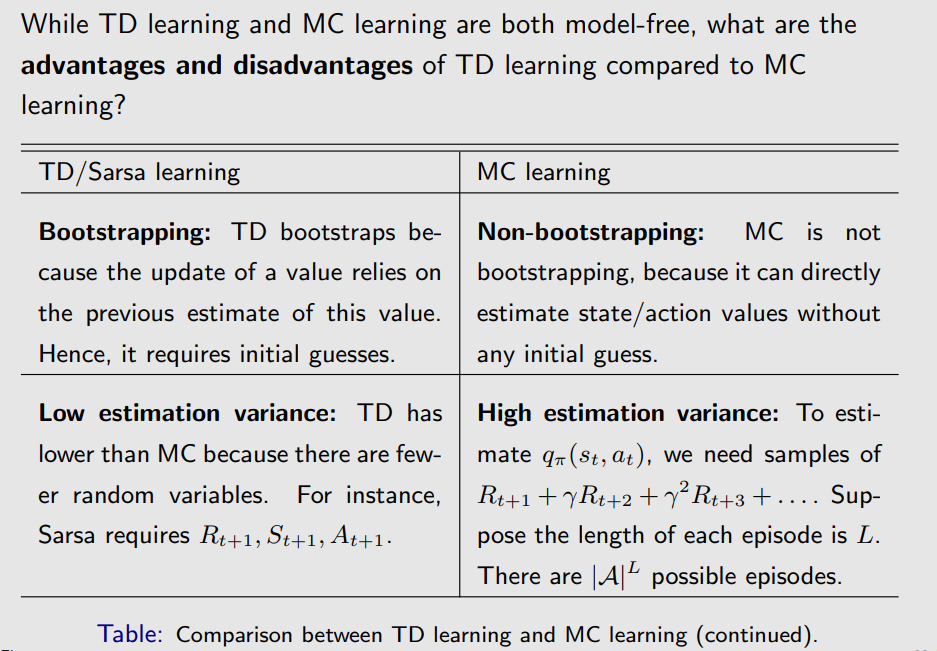
TD算法与MC算法的比较

TD算法是在线的，可以立刻用得到的信息更新数据，因此可以解决一些Continuing tasks，同时相比MC算法由估计结果有更低的方差。

Sarsa算法的收敛性

与TD算法证明类似。

Sarsa算法的伪代码

相比TD，Sarsa算法和policy improvement相结合，这里采用的是$ϵ$-greedy policy。

Q-learning

Q-learning与前面两个算法不同的是它是直接对贝尔曼最优方程进行求解。

Q-learning算法如下：
$$\begin{array}{rl}{q}_{t+1}(s_t,a_t)& =q_t(s_t,a_t)-{\alpha }_t(s_t,a_t)\lfloor q_t(s_t,a_t)-[r_{t+1}+\gamma \underset{a\in \mathcal{A}}{\max }{q}_t(s_{t+1},a)]\rfloor ,\\ q_{t+1}(s,a)& =q_t(s,a),\forall (s,a)\ne (s_t,a_t),\end{array}$$
与Sarsa算法类似，唯一的不同点就是Q-learning的TD target是$r_{t+1}+\gamma {\max }_{a\in \mathcal{A}}{q}_t(s_{t+1},a)$。
Q-learning算法求解的是关于动作值函数的贝尔曼最优方程：$$q(s,a)=\mathbb{E}\left[R_{t+1}+\gamma \underset{a}{\max }q(S_{t+1},a)\right|S_t=s,A_t=a],\forall s,a.$$

on-policy learning and off-policy learning

如下是Q-learning 两种不同版本的伪代码（on-policy learning and off-policy learning）

参考资料

课程《强化学习的数学原理》 赵世钰教授 西湖大学