强化学习——贝尔曼最优方程

本篇博客内容源于课程《强化学习的数学原理》 赵世钰老师 西湖大学，旨在记录学习强化学习的过程。

文章脉络：贝尔曼最优方程实际上就是贝尔曼方程的特殊情况，特殊在策略不再是给定的，而是转化为一个最优化问题所需要求解的未知量，贝尔曼最优方程所涉及的函数实际上是一个压缩映射，压缩映射定理为贝尔曼最优方程解的存在性和唯一性提供理论支持，并由相应的迭代算法可以找到方程的解，可以证明找到的解$v_{\ast }$以及伴生的贪婪策略${\pi }^{\ast }$具有最优性。

如何描述不同策略的优劣性？

描述不同策略的优劣性从对应策略的状态值函数出发：

根据上述描述方法我们可以得到最优策略${\pi }^{\ast }$对于其他任何策略$\pi$以及任何状态$s$，满足：$$v_{{\pi }^{\ast }}(s)\ge v_{\pi }(s)$$

什么是贝尔曼最优方程（BOE）？

开门见山，贝尔曼最优方程实际上就是贝尔曼方程的特殊情况，特殊在策略不再是给定的，而是转化为一个最优化问题所需要求解的未知量，贝尔曼最优方程长这样，：

向量形式的贝尔曼最优方程：

如何求解贝尔曼最优方程？

压缩映射定理

首先引入压缩映射定理
思路就是证明依据算法构造出的点列是一个收敛的柯西列。
1. 证明存在性

构造点列 { x k } \{x_{k}\} {xk​}，满足$x_{k+1}=f(x_k)$，由于$f$是压缩映射（满足$\forall x_1,x_2,\exists \gamma \in (0,1)，s.t.||f(x_1)-f(x_2)||\le \gamma ||x_1-x_2||$），所以
$\forall m\ge n$

显然$||x_1-x_2||$是有界的，$\frac{{\gamma }^n}{1-\gamma }$趋于0，易知依据算法构造的点列是一个柯西列，$x_{k+1}=f(x_k)$两边取极限就有$x^{\ast }=f(x^{\ast })$，我们要找的不动点其实就是点列 { x k } \{x_{k}\} {xk​}的极限值。（柯西列不一定是收敛的）
2. 证明唯一性
假设存在其他不动点$x^{\prime }\ne x^{\ast }，x^{\prime }=f(x^{\prime })$，那么有

因为$\gamma \in (0,1)$，先不等式成立当且仅当$||x^{\prime }-x^{\ast }||=0$，推出$x^{\prime }=x^{\ast }$，矛盾。

关于贝尔曼最优方程的函数是一个压缩映射

求解贝尔曼最优方程

根据压缩映射定理我们可以说明贝尔曼最优方程解的存在性和唯一性。

根据理论证明，并依据给出的迭代算法能找到解：


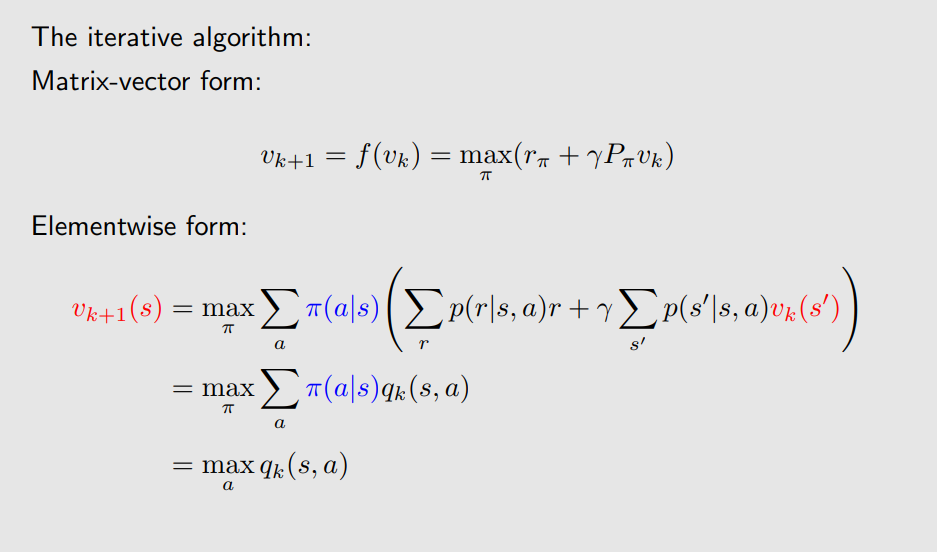
方程的解$v_{\ast }$以及相应经过迭代得到的策略${\pi }^{\ast }$是否就是最优的呢？，下一节给出解答。

贝尔曼最优方程的解以及伴生策略的最优性

假定求出贝尔曼最优方程的解为$v^{\ast }$,对应策略为${\pi }^{\ast }={\mathrm{argmax}}_{\pi }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$，那么有

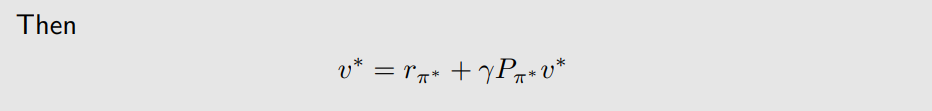
下面的定理将说明$v^{\ast },{\pi }^{\ast }$具有最优性：

证明如下：

已经证明了${\pi }^{\ast }$具有最优性，那么${\pi }^{\ast }$长什么样呢？实际上在每一步策略迭代中，由于${\sum }_a\pi (a|s)=1$，自然在最优化问题当中应当选择在状态$s$下动作值函数$q^{\ast }(s,a)$最大的所对应的动作$a$，因此这样得到的策略也被叫做贪婪策略（Greed Plicy，不给其他动作一点机会）。

什么因素会影响最优策略？

从BOE的表达式可以清晰地看到，$r,\gamma$都会影响最优策略。

参考资料

课程《强化学习的数学原理》 赵世钰教授 西湖大学