极大似然估计是一种概率论在统计学中的应用,建立在极大似然原理的基础上,极大似然原理的直观解释是:一个随机试验如有若干个可能的结果A、B、C、…,若在一次试验中,结果A出现,则一般认为试验条件对A出现有利,也即A出现的概率很大,那么就取参数估计,使A出现的概率最大。
设随机变量Y具有概率密度函数



为了计算方便,我们通常求使


在观测样本已知的情况下,N是定值,那么,极大似然估计

衡量两个分布g(·)和f(·|θ)差异性的统计量KL散度(或者相对熵)为:
只有当g(y)等于f(y|θ)时,KL散度才为0,因此,当随机变量Y给定时,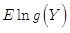
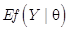
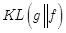
KL-divergence,俗称KL距离,常用来衡量两个概率分布的距离。
根据shannon的信息论,给定一个字符集的概率分布,我们可以设计一种编码,使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X,对x∈X,其出现概率为P(x),那么其最优编码平均需要的比特数等于这个字符集的熵:
H(X)=∑x∈XP(x)log[1/P(x)]=-∑x∈XP(x)log(p(x))
在同样的字符集上,假设存在另一个概率分布Q(X)。如果用概率分布P(X)的最优编码(即字符x的编码长度等于log[1/P(x)]),来为符合分布Q(X)的字符编码,那么表示这些字符就会比理想情况多用一些比特数。KL-divergence就是用来衡量这种情况下平均每个字符多用的比特数,因此可以用来衡量两个分布的距离。即:
DKL(Q||P)=∑x∈XQ(x)[log(1/P(x))] - ∑x∈XQ(x)[log[1/Q(x)]]=∑x∈XQ(x)log[Q(x)/P(x)]
由于-log(u)是凸函数,因此有下面的不等式
DKL(Q||P) = -∑x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = -log∑x∈XQ(x)P(x)/Q(x) = 0
即KL-divergence始终是大于等于0的。当且仅当两分布相同时,KL-divergence等于0。
===========================
举一个实际的例子吧:比如有四个类别,一个方法A得到四个类别的概率分别是0.1,0.2,0.3,0.4。另一种方法B(或者说是事实情况)是得到四个类别的概率分别是0.4,0.3,0.2,0.1,那么这两个分布的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)
这个里面有正的,有负的,可以证明KL-Distance()>=0.
从上面可以看出, KL散度是不对称的。即KL-Distance(A,B)!=KL-Distance(B,A)
KL散度是不对称的,当然,如果希望把它变对称,
Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2










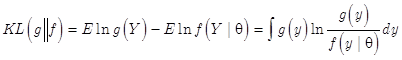














 724
724

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








