从拉格朗日插值法到范德蒙行列式

最新推荐文章于 2025-03-02 19:58:31 发布

马同学图解数学

最新推荐文章于 2025-03-02 19:58:31 发布

阅读量5.5k

点赞数 7

分类专栏：人工智能文章标签：插值法拉格朗日插值法范德蒙行列式

本文链接：https://blog.csdn.net/ccnt_2012/article/details/82254575

版权

人工智能专栏收录该内容

23 篇文章

订阅专栏

之前我写过一篇文章：如何理解牛顿插值法？其中解释了什么是插值法？为什么要有插值法？大家对此感兴趣可以去看看。

还有另外一种插值法，叫做拉格朗日插值法，也是以大牛冠名的，我们来看看它是怎么推导的？

1 拉格朗日插值法

比如说，已知下面这几个点，我想找到一根穿过它们的曲线：

使用多项式画出这根曲线是完全可行的，关于这点可以参看我写的如何理解泰勒公式？。

我们可以合理的假设，这根曲线是一个二次多项式：

y = a_0 + a_1x + a_2x^2

这是因为有三个已知的点，可以通过下列方程组解出这个二次多项式：

$\begin{cases} y_1 = a_0 + a_1x_1 + a_2x_1^2\\ y_2 = a_0 + a_1x_2 + a_2x_2^2\\ y_3 = a_0 + a_1x_3 + a_2x_3^2\end{cases}$

不过这里不打算通过解方程来得到这根二次曲线，我们来看看拉格朗日是怎么解出这根曲线的？

1.1 拉格朗日的思考

约瑟夫·拉格朗日伯爵（1736 － 1813），可能是这么思考的。

首先，肯定得是二次曲线，这个之前我们就已经说明过了。

其次，拉格朗日认为可以通过三根二次曲线相加来达到目标。那这是怎么的三根二次曲线呢？

第一根曲线 f_1(x) ，在 x_1 点处，取值为1，其余两点取值为0：

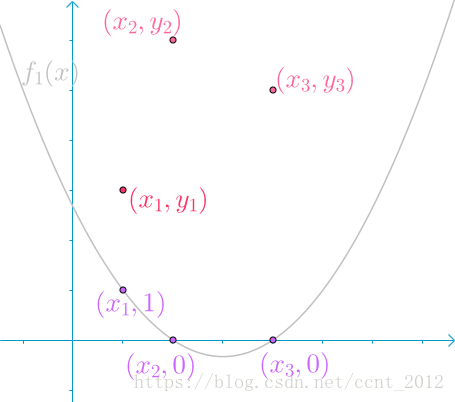
为什么这么做？看下去就知道了。

第二根曲线 f_2(x) ，在 x_2 点处，取值为1，其余两点取值为0：

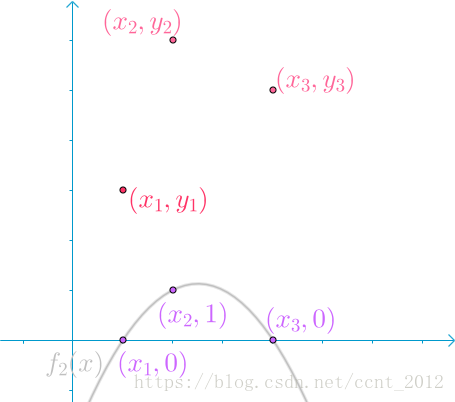
第三根曲线 f_3(x) ，在 x_3 点处，取值为1，其余两点取值为0：

这三根曲线就是拉格朗日需要的，我们来看看为什么？

可以保证，在点处，取值为，其余两点取值为0。
可以保证，在点处，取值为，其余两点取值为0。
可以保证，在点处，取值为，其余两点取值为0。

那么：

f(x)=y_1f_1(x)+y_2f_2(x)+y_3f_3(x)

可以一一穿过这三个点，我们来看看：

此处有互动内容，点击此处前往操作。

拉格朗日伯爵说，看，这三根曲线就可以组成我在寻找的曲线：

真的是非常精彩的思考啊。

1.2 插值法的推导

到了严格化的时候了，我们用符号来表示 f_i(x_j),i=1,2,3,j=1,2,3 。

首先， f_i 必须是二次函数。

其次，需要满足的条件：

$f_i(x_j)=\begin{cases}1&i=j\\0&i\ne j\end{cases}$

那么，如下构造 f_1(x) 很显然可以满足上述条件（代值进去就可以验算）：

$\displaystyle f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}$

更一般的有：

$\displaystyle f_i(x)=\prod_{j\ne i}^{1\leq j \leq 3}\frac{(x-x_j)}{(x_i-x_j)}$

因此，最终我们得到：

$\displaystyle f(x)=\sum_{i=1}^3 y_if_i(x)$

这就是拉格朗日插值法。上面的思路要推广到更多点的插值也非常容易。

牛顿插值法也是多项式插值法，拉格朗日插值法也是多项式插值法，那么，两者得到的多项式是否是同一个多项式？

2 拉格朗日插值法、牛顿插值法、范德蒙行列式

要回答刚才提出的问题，得看看我们最早提出的方程组怎么解？

$\begin{cases} y_1 = a_0 + a_1x_1 + a_2x_1^2\\ y_2 = a_0 + a_1x_2 + a_2x_2^2\\ y_3 = a_0 + a_1x_3 + a_2x_3^2\end{cases}$

(x_1,y_1),(x_2,y_2),(x_3,y_3) 这三个点是已知的，所以上面实际是一个线性方程组：

$\underbrace{\begin{pmatrix}y_1\\y_2\\y_3\end{pmatrix}}_{\vec{y}}=\underbrace{\begin{pmatrix}1&x_1&x_1^2\\1&x_2&x_2^2\\1&x_3&x_3^2\end{pmatrix}}_{A}\underbrace{\begin{pmatrix}a_0\\a_1\\a_2\end{pmatrix}}_{\vec{a}}$

简写就是：

$\vec{y}=A\vec{a}$

就是所谓的范德蒙矩阵， |A| 自然就是范德蒙行列式。

根据矩阵与线性方程组解的关系，如果 $|A|\ne 0$ ，那么此方程就只有唯一的解，自然牛顿插值法、拉格朗日插值法得到的就是同一根多项式曲线。

求一下 |A| ，先把 r_2-r_1,r_3-r_1 ，得到（ r_1 表示第一行，以此类推。这么做是不会改变行列式的值的）：

$\begin{align*} |A|&=\begin{vmatrix}1&x_1&x_1^2\\0&x_2-x_1&x_2^2-x_1^2\\0&x_3-x_1&x_3^2-x_1^2\end{vmatrix}\\ &=\begin{vmatrix}x_2-x_1&x_2^2-x_1^2\\x_3-x_1&x_3^2-x_1^2\end{vmatrix}\\ &=(x_3-x_1)(x_3-x_2)(x_2-x_1)\end{align*}$