GCN推导合集

读论文,发现看论文最重要的是推导,因此写了这篇文章,记录重要的推导过程(个人人为的)(持续更新)

SGC以及最常见优化的推到

邻接矩阵归一化:$$\tilde{A}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$$
对应::
$$A=I_n+D^{-1/2}A{D}^{-1/2}$$
是低通过滤器,
$$L=I_n-D^{-1/2}A{D}^{-1/2}$$
相应的是高通滤波器
参考:https://blog.csdn.net/qq_51392112/article/details/129105003
A的特征值范围是[-1,1],L的特征值范围为:[0,2]
由于图附近的信号应该是平滑的,我们有如下的定义光滑信号:
$$\underset{H}{\min }\Vert H-X{\Vert }_F^2+s\mathrm{Tr}\left({\mathrm{H}}^{\top }\mathrm{LH}\right)\text{\hspace{1em}(1)}$$
其中,
$$O_{reg}=\frac{1}{2}\sum _{i,j}^n{\tilde{\mathbf{A}}}_{i,j}\Vert {\mathbf{H}}_i-{\mathbf{H}}_j{\Vert }^2=tr({\mathbf{H}}^T\tilde{\mathbf{L}}\mathbf{H})\text{\hspace{1em}(2)}$$
(如上公式基于图相邻的节点应该是平滑的,因此当i和j有连边的时候,$H_i-H_j$应该尽可能的小)
推导如下图:

由公式1求导后得:
$$H=(I+sL{)}^{-1}X$$
泰勒公式展开(一阶)得:
$$H=(I-sL)X$$
m阶为:$$H=(I-sL{)}^{m}X$$

卷积核 来自大佬SivilTaram

卷积概念

卷积是定义在两个函数(f和g)上的数学操作.f和g上的卷积可以写为$f\ast g$.数学定义如下:
$$(f\ast g)(t)={\int }_{-\infty }^{\infty }f(\tau )g(t-\tau )(\text{连续形式})$$
$$(f\ast g)(t)=\sum _{\tau =-\infty }^{\infty }f(\tau )g(t-\tau )(\text{离散形式})$$

我们可以参考如下去理解:
假如有两个骰子f,g,f(1)表示f朝上一面为1的概率.同时抛两个筛子1次,它们正面朝上数字为4的概率为:

• f上1,g上3
• f上2,g上2
• f上3,g上1
  即:
  $$\sum _{\tau =1}^{3}f(\tau )g(4-\tau )$$
  在图领域,g可以看做深度学习中的核(kernel),也就对应滤波器.f可以对应深度学习中的特征.$(f\ast g)$就可以对应对f的加权求和
  

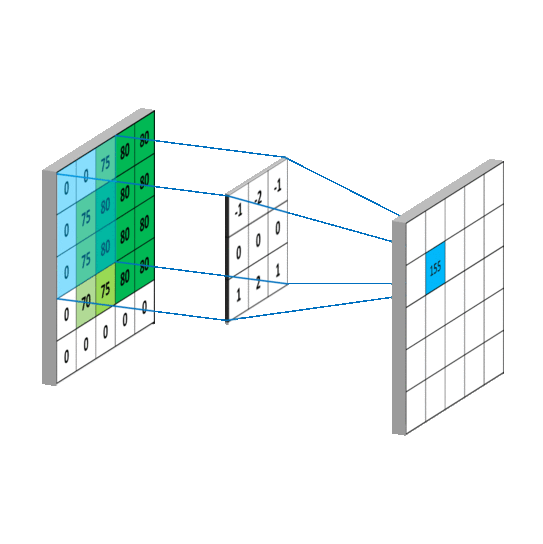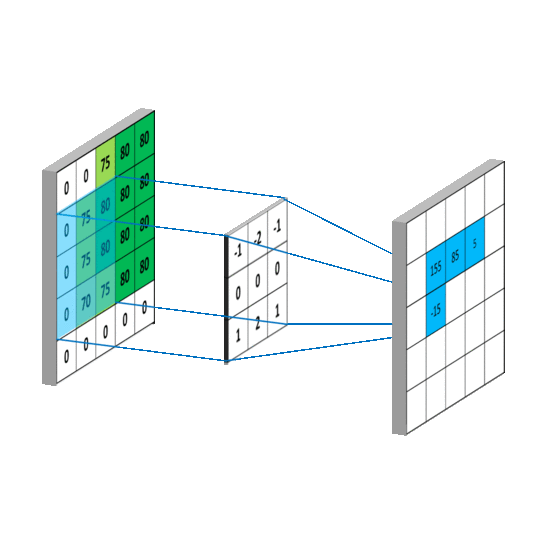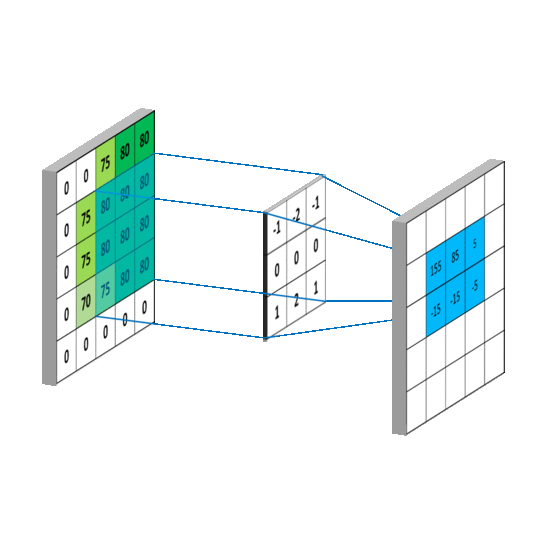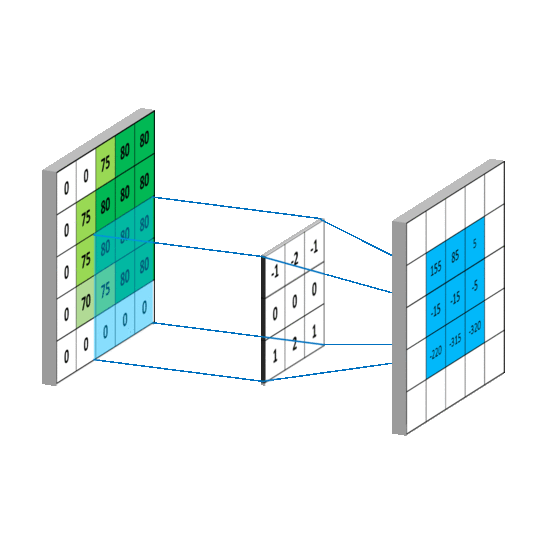
空间卷积

消息传递函数:
$${\mathbf{h}}_v^{l+1}=U_{l+1}({\mathbf{h}}_v,\sum _{u\in ne[v]}{M}_{l+1}({\mathbf{h}}_v^l,{\mathbf{h}}_u^l,{\mathbf{x}}_{vu}))$$

傅里叶变换(Fourier Transform)

$$(f\ast g)(t)=F^{-1}[F[f(t)]\odot F[g(t)]]$$
$F^{-1}$是傅里叶逆变换,$\odot$指的是两个矩阵的逐点乘积(hadamard积)
简单来说就是，如果要算 f𝑓 与 g𝑔 的卷积，可以先将它们通过傅里叶变换变换到频域中，将两个函数在频域中相乘，然后再通过傅里叶逆变换转换出来，就可以得到 𝑓 与 𝑔 的卷积结果。
傅里叶变换后生成的
$$\hat{f}\left(t\right)=\int f(x){\exp }^{-2\pi ixt}dx$$
${\exp }^{-2\pi ixt}$相当于拉普拉斯算子$△$的广义特征函数
$$\Delta {\exp }^{-2\pi ixt}=\frac{{\partial }^2}{\partial t^2}{\exp }^{-2\pi ixt}=-4{\pi }^2{x}^2{\exp }^{-2\pi ixt}$$
这意味着,傅里叶变换将$f(t)$映射到了 { exp ⁡ − 2 π i x t } \{\exp^{-2\pi ixt}\} {exp−2πixt}为基的空间中

图上卷积

$$L=U\Lambda U^T$$
$$U=(u_1,u_2,\cdots ,u_n)$$
$$\Lambda =\left[\begin{array}{ccc}{\lambda }_1& \dots & 0\\ & & \\ \dots & \dots & \dots \\ 0& \dots & {\lambda }_n\end{array}\right]$$
结合上面的卷积和傅里叶变换的公式,图上卷积公式(即傅里叶变换):
$$\hat{f}\left(t\right)=\sum _{n=1}^{N}f(n)u_t(n)$$
如果整个图上N个节点一起做卷积,就可以得到整张图的卷积:
$$\hat{f}=\left[\begin{array}{c}\hat{f}\left(1\right)\\ \dots \\ \hat{f}\left(N\right)\end{array}\right]=U^{T}f$$
我们将图上卷积公式代入卷积公式中:
$$(f{\ast }_{G}g)=U(U^{T}f\odot U^{T}g)=U(U^{T}g\odot U^{T}f)$$
如果把$U^{T}g$整体看做可学习的卷积核,这里我们把它写作$g_{\theta }$,最终图上的卷积公式:
$$o=(f{\ast }_{G}g{)}_{\theta }=U{g}_{\theta }{U}^{T}f$$

附录部分

常见矩阵求导法则:
$$\frac{\partial tr(AB)}{\partial A}=B^T$$
$$\frac{\partial tr(AXB)}{\partial X}=(BA{)}^T=A^T{B}^T$$
$$\frac{\partial tr(X^{T}X)}{\partial X}=2X$$
$$\mathrm{tr}(A)=\mathrm{tr}(A^T)$$