GNN之GCN基础理论推导

最新推荐文章于 2024-07-01 19:10:31 发布
最新推荐文章于 2024-07-01 19:10:31 发布
阅读量1.5k 收藏 4
点赞数 1
分类专栏： GNN
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_43330946/article/details/102833249
版权
本文介绍了图卷积网络GCN的基础理论，包括卷积的数学定义，如何在图结构上应用Fourier变换解决计算问题，以及Laplacian算子在图信号处理中的作用。通过对卷积定理的证明，阐述了在图数据上进行卷积运算的方法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

图卷积graph convolutional network，简称GCN，最近几年大热，取得不少进展。

清华大学孙茂松教授组发布了Graph Neural Networks: A Review of Methods and Application，对现有的GNN模型做了详尽且全面的综述。

针对GCN中需要的基础理论知识，这里给出数学推导，方便理解。

一、什么是Convolution

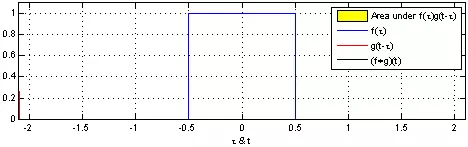
Convolution的数学定义是：

(f\ast g)(t)= \int _{R} f(x)g(t-x)dx，一般称g为作用在f上的filter或kernel。

常见的CNN二维卷积示意图如下：

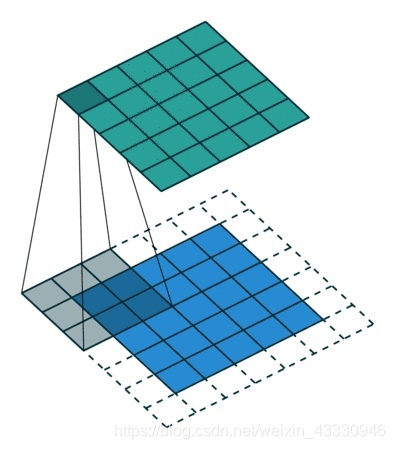
在图像（image）里，卷积的概念很直接，因为像素点的排列顺序有明确的上下左右的位置关系。

但是在抽象的graph里，有的节点会关联上万的节点，这些节点没有空间上的位置关系，也就没办法通过上面的传统卷积公式进行计算。

二、Fourier变换

为了解决graph上卷积计算的问题，需要用到Fourier变换。

根据卷积定理，卷积公式还可以写成：f\ast g = \mathit{F}^{-1}\{F\{f\}}\cdot F\{g\}\} ，这样只需要定义graph上的fourier变换，就可以定义出graph上的convolution变换。

首先，看一下Fourier变换的定义：

F\{f\}(v) = \int _{\mathbb{R}}f(x) e^{-2\pi ix \cdot v} dx

Inverse Fourier变换则是：

最低0.47元/天 解锁文章
B.图算法：图学习之图神经网络GNN模型GCN、GAT[系列六]
丨汀、的博客
11-18 1341
ICLR2023的评审结果已经正式发布！今年的ICLR2023共计提交6300份初始摘要和4922份经过审查的提交，其中经过审查提交相比上一年增加了32.2%。在4922份提交内容中，99%的内容至少有3个评论，总共有超过18500个评论。按照Open Review评审制度，目前ICLR已经进入讨论阶段。官网链接：https://openreview.net/group?1、AI应用应用，例如：语音处理、计算机视觉、自然语言处理等2、深度学习和表示学习3、通用机器学习4、生成模型。
图卷积网络Graph Convolutional Network（GCN）的理解和详细推导.pdf
06-11
图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导博客pdf 原博客链接：https://blog.csdn.net/yyl424525/article/details/100058264#comments_12499724
GCN推导
这个人很蓝
02-17 1636
GCN涉及到的理论比较多，包括信号分析、图谱等理论，要理解掌握所有概念比较难，必须承认有些概念我也只是大概看懂但理解还不是特别透彻，所以只在这里做一个简单的推导，有错误的地方还请指出，十分感谢。 由于图是不规则化的非欧式结构数据，而CNN是在欧式数据（如图片、语音等）上进行卷积，如何在不规则的图上定义卷积？我们从卷积定理入手。 卷积定理 卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积 这...
GCN推导合集
chairuilin的博客
07-01 2182
读论文,发现看论文最重要的是推导,因此写了这篇文章,记录重要的推导过程(个人人为的)(持续更新)
图卷积GCN推导
weixin_41149572的博客
02-03 409
图卷积 预备知识： a. 傅里叶变换 F(f)(v)=∫Rf(x)e−2πix⋅vdxF−1(f)(x)=∫Rf(v)e2πiv⋅xdv F(f)(v)=\int _{R}f(x)e^{-2\pi ix\cdot v}dx \qquad F^{-1}(f)(x)=\int _{R}f(v)e^{2\pi iv\cdot x}dvF(f)(v)=∫R​f(x)e−2πix⋅vdxF−1(f)(x)=∫R​f(v)e2πiv⋅xdv b. 卷积 h(z)=∫Rf(x)g(z−x)dxh(z)=\int_{R}f
GNN 系列：图神经网络的“开山之作”GCN模型
Datawhale
08-04 2960
c点击上方“Datawhale”，选择“星标”公众号 第一时间获取价值内容 【导读】这是我们介绍图神经网络的第一篇文章，取自Kipf et al. 2017，文章中提出的模型叫Graph Convolutional Network(GCN)，个人认为可以看作是图神经网络的“开山之作”，因为GCN利用了近似的技巧推导出了一个简单而高效的模型，使得图像处理中的卷积操作能够简单得被用到图结构数据...
gcn实战_GNN 系列（二）：图神经网络的“开山之作”GCN模型
weixin_33781072的博客
12-31 1681
写在前面这是我们介绍图神经网络的第一篇文章，取自Kipf et al. 2017，文章中提出的模型叫Graph Convolutional Network(GCN)，个人认为可以看作是图神经网络的“开山之作”，因为GCN利用了近似的技巧推导出了一个简单而高效的模型，使得图像处理中的卷积操作能够简单得被用到图结构数据处理中来，后面各种图神经网络层出不穷，或多或少都受到这篇文章的启发。目录1、问题定义...
【GNN】万字长文带你入门 GCN
阿泽的学习笔记
05-21 1846
断断续续写了一个多星期，期间找了很多同学讨论学习，感谢指导过点拨过我的同学们，为了精益求精本着不糊弄别人也不糊弄自己的原则在本文中探讨了很多细节。 当然，还有很多细节没提到，包括总变差（Total Variation）、空域和频域视角下的图信号等，有兴趣的同学可以深入了解下图信号处理，本人才疏学浅还希望抛砖引玉引出更多的 GCN 的文章。 非常感谢知乎 @superbrother 同学和蘑菇先生的精彩笔记才使得我能够入门 GCN，当然我也将公开我的笔记希望能帮助更多的同学。 1. Convolutional
详解GCN原理-公式推导
SperNijia的博客
06-12 6501
GNN survey convolution 如何graph domain 上做convolution 是最近最热门的研究方向。 总的来说有两种卷积的方法： Spectral and non-spectral (spatial) spectral Network 通过对图的拉普拉斯矩阵做特征分解，将它定义在 傅里叶 domain上。 在深入解释之前，先看一些有关图的定义，以下都是针对无向图所做的说明 对于图GGG,可以用它其中的节点VVV 和 边EEE来对他进行定义。 矩阵AAA是图的邻接矩阵，反应了节点
GCN图卷积知识点和推导
09-26
mindmasterGCN图卷积笔记，内含公式推导以及相关知识，结构清晰，便于学习。
图卷积神经网络GCN中的关键公式推导---干货
生信小白一枚，欢迎大佬一起讨论分析前沿技术！
06-28 2384
1. 首先，定义图拉普拉斯矩阵 , 这里L可以换成任何其他形式，比如被正则化的拉普拉斯矩阵。2. 然后，对图进行卷积操作： 经过上述操作，可获得图上的卷积操作 3. 对图卷积公式进行简化求解，即求解。 4. 共享参数，即令，没啥道理，就是效果好才这样操作。最后公式可以整理为5. 最后，就可以训练卷积核了本文是整理b站一个大佬的视频笔记，从头到尾学习了一遍，感觉讲的很透彻，这里附上链接，感兴趣可以听一听：图卷积神经网络（GCN）的数学原理详解——谱图理论和傅立叶变换初探_哔哩哔哩_bilibi
图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导
热门推荐
知行合一，止于至善
08-24 16万+
文章目录1. 为什么会出现图卷积神经网络？2. 图卷积网络的两种类型2.1 vertex domain(spatial domain)：顶点域（空间域）2.2 spectral domain：频域方法（谱方法）3. 什么是拉普拉斯矩阵？3.1 常用的几种拉普拉斯矩阵普通形式的拉普拉斯矩阵对称归一化的拉普拉斯矩阵（Symmetric normalized Laplacian）随机游走归一化拉普拉斯矩...
学习：图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导
czp_374的博客
10-26 1070
复制链接
GNN、GCN原理及推导
liaominghui123的博客
07-19 2663
在这里插入图片描述 GNN分为两个角度去研究，一个空间域，一个谱域。 Spatial-based Conovolution 空间域的卷积就是空间上的卷积，跟CNN很像，就是综合一个节点的邻接节点的特征用来生成下一层的该点的特征然后整合成下一层的图： 1,NN4G 如上图，这里的卷积就是，对于v3来说，下一层的V3的特征就是一个参数（矩阵）乘以这一层的邻接点的特征，然后加上自己的特征与一个参数矩阵的乘积之后的输出跟CNN不一样，输出的y是前面所有层的平均然后分别乘以可训练矩阵后加起来得到： 为什么相加呢？可
GNN知识整理
hei_hei_hei_的博客
04-10 1588
目录 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. GCN 1.1基础公式： 符号解释 HlH^lHl表示第l层的输入特征； Hl+1H^l+1Hl+1表示输出特征； wlw^lwl表示线性变换矩阵； σσσ表示非线性激活函数； AAA表示邻接矩阵 A~\widetilde{A}A表示有自连的邻接矩阵，即A~=A+I\widetilde{A}=A+IA=A+I； D~\widetilde{D}D表示自连矩阵的度矩阵（对角矩阵：只有主对角线上元素有值，且第i行第i列的值等于A~\wi
【深度学习】最强算法之：图神经网络（GNN）
商务合作 | 面试培训 | 职场规划 ==>主页扫码
04-08 5464
深度学习必会算法之：GNN
Graph Neural Networks (GNN)（一）：Spatial-GNN
xiaopihaierletian的博客
11-28 967
Graph Neural Networks (GNN)（一）：Spatial-GNN
GNN和GCN的区别
最新发布
07-04
图神经网络 (GNN) 和 Graph Convolutional Networks (GCN) 都是用于处理图形数据的深度学习模型，但它们有一些核心区别： 1. **基础概念**: GCN 是 GNN 的一种具体实现，它是专门设计用来在图上进行卷积操作的。GCNs 将节点特征与邻居的信息相结合，形成新的表示。 2. **卷积操作**: 在传统的图像卷积中，每个滤波器（或称为核）对输入信号进行局部平移不变的操作。而在 GCN 中，"卷积核"被看作是邻接矩阵的一个列向量，这使得它们能够捕捉到图结构中的局部依赖关系。 3. **信息传递**: GCNs 通常通过一次或多次聚合邻域节点的信息来更新节点的特征。每次层迭代都会使信息逐渐从中心节点传播到整个图。 4. **简化形式**: GCN 简化了 Chebyshev 函数等更复杂的图卷积方法，直接采用一阶近似，避免了计算复杂度较高的高阶邻域信息。 5. **应用范围**: GCN 可以广泛应用于社交网络分析、推荐系统、化学分子建模等领域，而 GNN 更是一个更广泛的类别，包括但不限于 GCN，还可以扩展到更高级的架构如 GraphSAGE 或 GIN。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值