0)图的定义
图是由点和边组成的一种结构。
也就是说,图G=(V,E),V表示点的集合,E表示边的集合。而边也可以用点对来表示,即(v,w),其中v,w属于V。
如果点对(v,w)是有序的,也就是说(v,w)!=(w,v),那么我们就称图为有向图。
点v和w邻接,当且仅当(v,w)属于E。

1)图的附加概念
路径:路径由一系列点组成,这些点要满足一个约束条件,即相邻点要构成边。标准定义如下所示
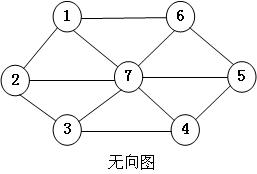
对于上面的有向图,一个路径的例子为1,7,4,3。
路径的长:边的个数,即为N-1。如果路径不包含边,则 length=0,这个 length=0的定义只是为了特例的方便。
有向图中路径1,7,4,3的长度为3.
环:是指存在(v,v)的边的图,那么这个路径称之为环,也就是说点自己指向自己,一般的图大多是无环的。
上面的例子是无环的。
简单路径:除了最初的点和最终的点可能是相同的点外,其余的点都是各不相同的,这样的路径称之为简单路径。
如:有向图中路径1,7,4,3。 无向图中路径1,7,6,1。
圈:在有向图中,一个长度至少为1的且点w1=wN的路径称之为圈。而对于无向图,我们要求边是不同的,因此,v,w,v不是一个圈,因为对于无向图(v,w)与(w,v)是同一条边。
在上面的有向图中没有圈的存在。无向图中是有很多圈的存在的,如1,2,3,4,5,6,1 。
无圈:没有圈的有向图称之为无圈图。
连通的:对于无向图,每一个点到任何一个其他点都有路径连通,称之为连通的。
强连通的:对于有向图,满足连通的条件的,称之为强连通的。
弱连通的:对于有向图,不满足强连通条件,但是其对应的无向图满足连通性条件。
完全图:对于有向图,每对点都有边连接。
上面的无向图是连通的,有向图是弱连通的,而不是强连通的,因为点2无法到达点1.
2)图的表示
这里我们说的图的表示是指图的存储,也就是说怎样用数据结构在计算机中存储图。
一个比较简单的想法是利用二维数组。即A[u][v]=1如果边(u,v)存在,A[u][v]=0如果边(u,v)不存在。这种方法可以表示有向图和无向图。
但是存在一个缺点,就是太耗费存储空间,因为大多数的图都是稀疏的,也就是说不是所有的两个点间都存在边。
因此为了节省空间,可以利用邻接链表来表示图,即利用链表来表示与一个点邻接的所有的点。
邻接链表法是最基本的表示图的方法,它的空间复杂度为O(|E|+|V|)。
对于上面的有向图,邻接链表的表示如下:
无向图的表示类似,只不过由于边没有方向,因此每条边会出现在两个链表中,使得存储空间加倍。








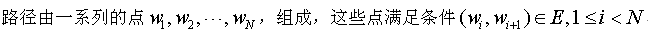
















 499
499

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








