在线 RMQ 算法介绍

一 点睛

两个节点的 LCA 一定是两个节点之间欧拉序列中深度最小的节点，寻找深度最小值时可以使用 RMQ 算法。

二 图解

欧拉序列指在深度遍历过程中把依次经过的节点记录下来，把回溯时经过的节点也记录下来.一个节点可能被记录多次，相当于从树根开始，一笔画出一个经过所有节点的回路。

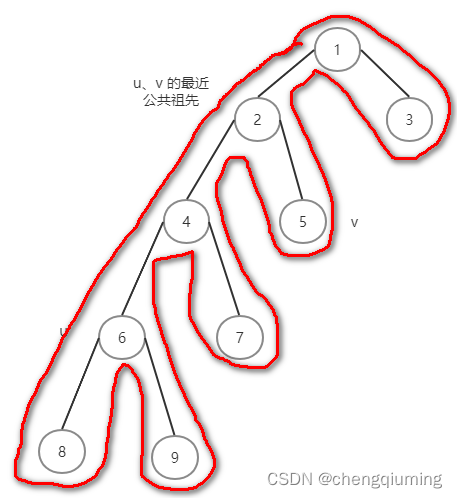
该树的欧拉序列为 1 2 4 6 8 6 9 6 4 2 5 7 5 2 1 3 1,搜索时得到 6 和 5 首次出现的下标  i、j，然后查询该区间深度最小的节点，为 6 和 5 号节点的最近公共祖先。

三 .算法实现

1 深度遍历，得到3个数组：首次出现的下标是 pos[],深度遍历得到的欧拉序列是 seq[]，深度是 dep[]。

2 根据欧拉序列的深度,创建区间最值查询的 ST。F(i,j) 表示[i,i+2^j-1] 区间深度最小的节点下标。

3 查询 [l,r] 区间深度最小的节点下标，与 RMQ 区间查询类似。

4 求 x 、y 的最近公共祖先，先得到 x 、y 首次出现在欧拉序列中的下标，然后查询该区间深度最小的节点的下标，根据下标读取欧拉序列的节点即可。