RNN 算法原理一（Recurrent Neural Network)

最新推荐文章于 2024-03-31 11:15:51 发布

明朝百晓生

最新推荐文章于 2024-03-31 11:15:51 发布

阅读量3.4k

点赞数

分类专栏：人工智能文章标签： rnn 算法 p2p

4AM_明朝百晓生

本文链接：https://blog.csdn.net/chengxf2/article/details/123051592

版权

人工智能专栏收录该内容

102 篇文章 3 订阅

订阅专栏

简介
模型结构
前向传播过程
反向传播BPTT 算法推导
算法实现

一简介

RNN 是一种时序链特征的循环神经网络。

主要应用于：

① 自然语言处理(NLP): 主要有视频处理, 文本生成, 语言模型, 图像处理

② 机器翻译, 机器写小说

③ 语音识别

④ 图像描述生成

对于时序链的特征预测. 最早一直用的是机器学习中的HMM,但是HMM缺点是观察值维度一般都是1个,准确率不是很高,也有用几个HMM加上集成学习来做的.

RNN主要架构如下：

二 One-to-One 模型结构

2.1 这里主要讲One-to-one 架构,有时候也成SRNN(simple RNN)

2.2 输入参数：

$x_t:$ t 时刻的输入值。 [n,1]的列向量

$h_t:$ t时刻神经输出,隐藏值。 [m,1]的列向量

$Z_t:$ t时刻神经元输入。 [m,1]的列向量

U: 输入值的权重系数。 [m,n]的矩阵

W: 隐藏值的权重系数。 [m,m]的矩阵

v: 输出值的权重系数. [k,m]的矩阵(分类模型）或者 [1,m]的行向量（股票预测）

$o_t$ : t 时刻的预测值. [k,1]的列向量,或标量（股票预测等）

$y_t$ : t 时刻的预测值。 [k,1]的列向量或标量（有的文档把这个作为标签值）

$\hat{y}_t$ : t 时刻的标签值。 [k,1] 的列向量，或标量

$L_t$ t 时刻的损失值。标量.分类数据用交叉熵连续型数据用MSE

2.3 前向传播（Forward）

公式1：      $Z_t = Ux_t+Wh_{t-1}+b$

公式2:    $h_t= tanh(Z_t)$

公式3:    $O_t=V h_t+C$

公式4：    $y_t= o_t$ (连续型数据） $y_t=softmax(o_t)$ (分类数据）

2.4 损失函数

$L=\sum_{t=1}^TL_t$

连续型数据

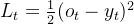
$L_t= \frac{1}{2}(o_t-y_t)^2$

$\frac{\partial L_t}{\partial o_t}=o_t-y_t$

分类数据：

$L_t= -(\hat{y_t}logy_t+(1-\hat{y_t})log(1-y_t)$

$\frac{\partial L_t}{\partial 0_t}=\frac{\partial L_t}{\partial y_t}\frac{\partial y_t}{\partial 0_t}=y_t-\hat{y_t}$

2.5 更新参数

输入层： W U,b

输出层： v,c

2.6 预测输出：

$y_t$

三算法推导方案一

3.1 输出层参数 V,C 梯度更新

$\frac{\partial L}{\partial V} = \sum_{t=1}^T\frac{\partial L_t}{\partial V}$

标量都矩阵求导：

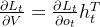
公式5： $\frac{\partial L_t}{\partial V} = \frac{\partial L_t}{\partial o_t}h_t^T$ $= (y_t-\hat{y_t})h_t^T$ (标量对矩阵链式求导）

公式6： $\frac{\partial L_t}{\partial c}=(\frac{\partial 0_t}{\partial c})^T(\frac{\partial L_t}{\partial o_t})$ $=E*(\hat{y_t}-y_t)=y_t-\hat{y_t}$ (标量对向量链式求导）

3.2 输入层参数 U 梯度更新

$\frac{\partial L}{\partial U} = \sum_{t=1}^{T}\frac{\partial L_t}{\partial U}$

有两种计算方法：

方法一：论文原注：

$\frac{\partial L_t}{\partial U}=\frac{\partial L_t}{\partial y_t} \frac{\partial y_t}{\partial h_t}(\sum_{k=1}^{t}(\frac{\partial h_t}{\partial h_k}\frac{\partial h_k}{\partial U})$

$\frac{\partial L_t}{\partial W}=\frac{\partial L_t}{\partial y_t} \frac{\partial y_t}{\partial h_t}(\sum_{k=1}^{t}(\frac{\partial h_t}{\partial h_k}\frac{\partial h_k}{\partial W})$

其中

$\frac{\partial h_t}{\partial h_k}= \prod_{i=k+1}^t\frac{\partial h_i}{\partial h_{i-1}}$

3.3 梯度爆炸

$\frac{\partial h_t}{\partial h_k}= \prod_{i=k+1}^t\frac{\partial h_i}{\partial h_{i-1}}$

其中 $\frac{\partial h_i}{\partial h_{i-1}}=diag(1-h_i^2)W$ （前半部分行列式<1）

如果时序链特别长,|W|又比较大，会导致梯度爆炸。

解决方案

1：梯度剪裁

2： L1,L2 正规化,在损失函数中加上关于W的约束项

3.4 梯度消失

这种更容易出现。因为 $diag(1-h_i^2)$ <1

更新梯度的时候，因为丢失信息,比如预测电量，t4时刻恰好是周末，

前面2天都是工作日，t1 ,t2 也是周末信息更重要，导致W把噪声学习进去了

然后再前向传播的时候，loss会变的更大。

解决方案

$h_{t+1}=h_{t}+f(h_t+x_{t-1})$

比如激活函数还用tanh,这种梯度就不会消失了。

$\frac{\partial h_{t+1}}{\partial h_{t}}=E+diag(1-h_t^2)$

基于这种思想后面有LSTM等

四算法推导方案二 BPTT

上面算法比较复杂,为了计算简单了.

这里应用了一种递归的BPTT算法。

最后一个时刻的

$\delta_T=V^T(y_t-\hat{y_t})$

输出层的梯度跟上面是一样的。

则输入层的梯度：

$\frac{\partial L}{\partial W}=\sum_{t=1}^T( \frac{\partial h_t}{\partial z_t})^T\delta_t h_{t-1}^T$

$\frac{\partial L}{\partial U}=\sum_{t=1}^T( \frac{\partial h_t}{\partial z_t})^T\delta_t x_{t}^T$

$\frac{\partial L}{\partial b}=\sum_{t=1}^T( \frac{\partial h_t}{\partial z_t})^T\delta_t$

四伪代码

step1 前向传播

def Forward(T)

for t in range(1,T)

$z_t= Ux_t+Wh_{t-1}+b$

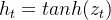
$h_t= tanh(z_t)$

   $o_t= Vh_t+c$

   $y_t= softmax(o_t)$

step2 BPTT 更新梯度

def BPTT(T)

=========计算梯度==========

for t in range(T,1)

if t== T

       $\delta_T=V^T(y_t-\hat{y_t})$

else

$\delta_t=W^Tdiag(1-h_{t+1}^2)\delta_{t+1}+v^T(y_t-\hat{y_t})$

-----------更新输入出层------------

$\Delta_V=\Delta_V+\frac{\partial L_t}{\partial V}=\Delta_V+(y_t-\hat{y_t})h_t^T$

    $\Delta_c= \Delta_c+\frac{\partial L_t}{\partial c}=\Delta_c+(y_t-\hat{y_t})$

------ 更新输入层

$\Delta_W=\Delta_W+diag(1-h_t^2)\delta_th_{t-1}^T$

$\Delta_U=\Delta_U+diag(1-h_t^2)\delta_t x_{t}^T$



=========更新梯度###############

$W= W-\Delta_W$

$U= U-\Delta_U$

$b= b-\Delta_b$

   $V= V-\Delta_V$

   $c= c-\Delta_W$

def Train()

注意这里面是单样本，如果多个样本piece,要分别求出来，再求一个均值，计算量

非常大。

for it in max iter(最大迭代次数)

Forward(T) #前向传播#

BPTT(T) #反向传播#

五代码实现

学习率要用小一点

# -*- coding: utf-8 -*-
"""
Created on Fri Mar  4 16:13:37 2022

@author: chengxf2
"""
import numpy as np
import matplotlib.pyplot as plt
import os
from enum import Enum

class MatType(Enum):
    
     RAND = 1  # 随机矩阵
     EYE =2   #单位矩阵
     ZERO = 3  # 0矩阵

'''
生成矩阵
args
  m: 行
  n: 列
return  
   矩阵
'''
def make_mat(m,n,tp:MatType):
    
    if tp is MatType.ZERO: 
        D = np.zeros((m,n))
    elif tp is MatType.RAND:       
        D = np.random.rand(m,n)
    else:
        D = np.eye(m)
        
    
    return np.mat(D)
    
class RNN():
    
    '''
    绘制loss
    args
       loss 列表
    '''
    def DrawLoss(self, loss):
        
        n = len(loss)

        x = np.arange(1,n+1)    
        plt.plot(x, loss, 'r--', label = 'aa')
        plt.xlabel('t')
        plt.ylabel('loss')
        plt.title('this is a demo')
        plt.legend() # 将样例显示出来


        plt.show()
    '''
    初始化模型参数
     args
        None
        
    '''
    def init_para(self):
        self.u = make_mat(self.hidden_size, self.input_size,MatType.RAND) #输入层权重系数
        self.w = make_mat(self.hidden_size, self.hidden_size,MatType.RAND)   #隐藏层的权重系数,防止生成行列式太小的导致梯度消失
        self.v = make_mat(1,self.hidden_size,MatType.RAND) #输出层的权重系数
        self.b = make_mat(self.hidden_size,1,MatType.RAND)  #输入层偏置
        self.c = 0.05 #输出层偏置
        
    '''
    获得梯度
    输入
       H: [m,1]向量
    输入
       矩阵
    '''
    def GetDelta(self, H):
        
        m,n = np.shape(H)
        D = np.eye(m)
        
        for i in range(m):
            a = H[i,0]
            D[i,i]= 1.0-a**2
        #print("\n D ",D)
        return np.mat(D)
    
    '''
    打印出Dict
    '''
    def PrintDict(self,dictH:dict):
        
        for key in dictH.keys():
            
            D = dictH[key]
            
            print("\n ---key----\n"%key,D)
         
    
    

   
    '''
    dict_h：  隐藏值
    predictList: 预测值
    trainLabel:  标签值
    args
        None
    return
        None
        trainData,dict_h,dict_y,trainLabel
    '''
    def bptt(self,trainData, dict_h,dict_y,trainLabel):
        
       
         
        delta_u = make_mat(self.hidden_size,self.input_size,MatType.ZERO)#输入U的权重系数
        delta_w = make_mat(self.hidden_size,self.hidden_size,MatType.ZERO)#输入w的权重系数
        delta_v = make_mat(1,self.hidden_size,MatType.ZERO)#输出层v的权重
        delta_b = make_mat(self.hidden_size,1,MatType.ZERO)#输入b的权重
        delta_c = 0.5 #输出层的偏置
        
        delta_t = None # L对t时刻h的偏导数
        delta ={} #保存h的梯度

     
        for t in reversed(np.arange(0,self.T)):
    
            t_y   =  dict_y[t]       #t时刻的预测值
            t_label =  trainLabel[t] # t时刻的标签值
            diff_t =    t_y-t_label  #t时刻的loss
            delta_t_t = self.v.T*diff_t # Lt对ht求偏导数 

            
            if t == (self.T-1): #最后一个时刻
               #print("\n--------T-1--------------",t)
               delta_t = delta_t_t
            else:
               h_next = dict_h[t+1]
               D = self.GetDelta(h_next)
               delta_t_1 = delta[t+1]  #t+1时刻对h(t+1)的偏导数
               delta_t  = delta_t_t+self.w.T*D*delta_t_1
            delta[t]= delta_t 
        #self.PrintDict(delta)
        
        for t in range(0,self.T):
            
            t_y =  dict_y[t]      #t时刻的预测值
            t_label = trainLabel[t] #t时刻的标签值
            t_diff =  t_y-t_label     #t时刻的loss
            
            
            
            h_t =   dict_h[t]     #当前时刻的隐藏值
            h_t_prv = dict_h[t-1] #t-1的隐藏值
            x_t = trainData[t]    #t时刻的输入的转置
            delta_t= delta[t]    #当前时候梯度
            
            

            dz = self.GetDelta(h_t)
            delta_t_z = dz*delta_t 
            #print(np.shape(dz),np.shape(delta_t),np.shape(delta_z))
            #输出层梯度更新
          
            
            #print("\n--------------------",diff)
            #print("\n---h_t---\n", h_t.T,"\n---e---\n",e)
            delta_v = delta_v + t_diff*(h_t.T)
            delta_c = delta_c + t_diff
            ###更新输入层
            A = delta_t_z*(h_t_prv.T)
            #print("\n ==t%d===\n"%t,A,"\t d ",np.linalg.det(A))
            delta_w = delta_w + A
            delta_u = delta_u + delta_t_z*x_t
            delta_b = delta_b + delta_t_z
            #print("\n delta_t ",delta_t)
        #print("\n ---u----\n",delta_u,"\n --w--\n",delta_w,"\n--v -\n",delta_v)

        #for a in [np.array(delta_w), np.array(delta_u), np.array(delta_b), np.array(delta_v), np.array(delta_c)]:
                # np.clip(a, -5, 5, out=a)
        return  delta_w, delta_u, delta_b,delta_v,delta_c
    

    
    
    '''
    前向传播
        trainData:  输入数据集
        trainLabel: 输入标签集
    return
        dict_h : 预测值
        dict_y:  隐藏值
        avgloss 损失
    '''
    def forWard(self,trainData,trainLabel):
        
        dict_h ={} #隐藏值
        dict_y ={} #预测值
        
        
        loss = 0.0
        h_0 = make_mat(self.hidden_size,1,MatType.ZERO)
        dict_h[-1]= h_0             

        
        for t in range(0,self.T):    
            x_t = trainData[t].T    #t时刻的输入   
            h_pre = dict_h[t-1]     #前一时刻的隐藏值
            z_t = self.u*x_t +self.w*h_pre+self.b #神经元输入
            h_t = np.tanh(z_t) #神经元输出
            y_t = np.dot(self.v,h_t)+self.c
         
            ####保存当前的参数####
            dict_h[t]=  h_t 
            dict_y[t] = y_t[0,0]
            #计算loss
            label = trainLabel[t]
            loss = loss+np.power(y_t[0,0]-label,2)
            #print("\n t: %d:  y_t %3.2f"%(t,y_t[0,0]))
        avgloss = loss/self.T 
        print("\n   loss=   %5.3f"%avgloss)   
        return dict_h,dict_y,avgloss
            
            
    '''
    从txt读取数据集，最后一列是标签   
    args:
        file_path:
    return
       trainData: 数据集矩阵 [T,input_size] 
       trainLabel: 数据集标签
    '''
    def readData(self):
        
    
        f =  open("data.txt", "r")
        
        lines = f.readlines()  # 读取文件
        trainData =[] #数据集
        trainLabel =[]  #标签
        
        for line in lines:
            
            item = line.split(",")
            data =[]
            data =  [float(a) for a in item]
            x = data[0:-1] 
            label = float(data[-1])
            trainData.append(x)
            trainLabel.append(label)
        f.close()
        
    
        
        return np.mat(trainData),trainLabel


    '''
    input_size:  x的维度
    hidden_size: h的维度
    
    '''
    def __init__(self,input_size=1, hidden_size=1,out_size =1,T=20,maxIter=300):
        
         self.maxIter = maxIter # 最大迭代次数
         self.T = T  #时间
         self.input_size = input_size
         self.hidden_size = hidden_size
         self.out_size = out_size
         self.learnRate = 0.2 #学习率
         
         
         
         
    
    def Train(self):
        rnn.init_para()
        trainData, trainLabel = rnn.readData()
        loss = []

        
      
        
        for i in range(self.maxIter):
            print("\n ===========迭代次数%d =========="%i)
            alpha = (1.0/self.T)*self.learnRate
            dict_h,dict_y ,avgloss = self.forWard(trainData,trainLabel) #前向传播
            delta_w, delta_u, delta_b,delta_v,delta_c =  self.bptt(trainData,dict_h,dict_y,trainLabel) #bptt
            
            #print("\n delta_v",delta_v,np.shape(delta_v))
            
            print("dev",np.linalg.det(self.w))
            
            #det = abs(np.linalg.det(self.w))
            
            
           
            
       
            self.w =  self.w-  alpha*delta_w
            self.u =  self.u-  alpha*delta_u
            self.b =  self.b-  alpha*delta_b
            self.v =  self.v-  alpha*delta_v
            self.c =  self.c-  alpha*delta_c
            
            
            a = np.linalg.det(delta_w)
            c = np.linalg.det(self.w)**self.T
            #a = np.sum(np.power(delta_w,2))
           
            
            loss.append(avgloss)
            #if avgloss-oldLoss<1e-6:
                #break
            #else:
                #oldLoss = avgloss
        self.DrawLoss(loss)  
        
        print("\n w: \n ",self.w)
        print("\n u: \n",self.u)
        print("\n b: \n",self.b)
            
            
        


if __name__ == "__main__":
      os.chdir(os.path.dirname(__file__))
      #,input_size=1, hidden_size=1,out_size =1,T=20,maxIter=300):
      rnn = RNN(3,6,1,10,1000)
      
      rnn.Train()