NR LDPC 03- Tanner

前言：

1963年,Gallager（麻省理工罗伯特·加拉格尔院士)在其博士论文中提出了LDPC码

1982年 Tanner 使用图来表示LDPC码,推广了LDPC码

LDPC属于线性分组码，常用校验矩阵或Tanner图来描述。

      使用校验矩阵可以看到 信息比特 和 校验比特之间的约束关系，编码过程用的多。

这里主要介绍一下Tanner 图

参考

Tanner图_百度百科

 

目录

1： Tanner 主要思想

2： Tanner 图

---

一 Tanner 图主要思想

   主要由三部分组成

   校验节点C(有的时候也称为监督节点）

   变量节点V, 边 三部分组成

校验节点： 代表 校验矩阵中的行                 

变量节点： 代表校验矩阵中的列，即编码bit

边： 校验节点对应行，以及 变量节点对应列位置为1， 如果为1 有变，否则无边

行度： 校验矩阵中某行1的个数和

列度： 校验矩阵中某列1的个数和

---

二 Tanner 图

  

   2.1 如下为LDPC 的校验矩阵（1的个数远远小于0的个数）

     

    

   : 为编码信息，前面3位为信息，后面为奇偶校验位

  2.2 Tanner 图

      

    校验节点：

           跟校验矩阵行对应，例如行2

           ,   是一个SPC code。

           这个也是LDPC算法的核心思想，把一个复杂的问题，分解成一系列最基本的

             spc code 求解。

     变量节点：

           跟校验矩阵列对应

     column Degree:

              列度数，该列中1的个数。

               看Tanner 图就是一个变量节点关联多少个校验节点

              LDPC码中 列重和行重非常小

     row Degree

               行度数， 该行中1的个数。

               也就是最小的SPC 结构。

---

三   Tanner 图解码例子

(n=9,k=4) 

3.1 奇偶校验矩阵H

3.2 Tanner 图

     收到的数据 为erase 状态，需要解码出来

   

 

3.3 第一轮迭代

  

 

   所有的变量节点V把信息发送到校验节点C,

校验节点根据收到的数据判断是否满足SPC 条件:

如果满足就可以把其中earse的信息校验出来，并且反馈回去。

第一轮校验可以把 解码出来为1、

  

3.4 第二轮迭代

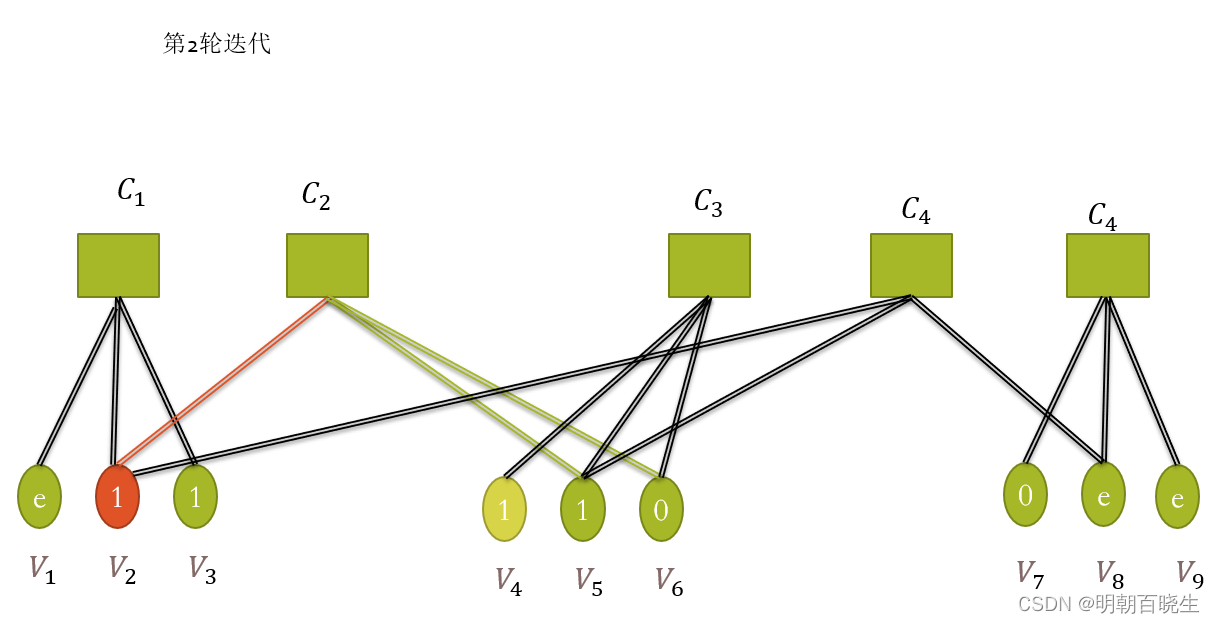.4 

 变量节点V 依然把信息发送到校验节点

 可以解码出,并反馈回变量节点 

 

3.5 第三轮迭代

解码出 

   

 

 3.6 第四轮迭代，解码出

     

 

   不同的校验矩阵设计会导致解码效率差别很大。

因为可以并行解码，所以解码速度会比Polar高很多

         

Iterative Methods

    Okay, so let's continue from where we had left off last time
. so this is the entire idea behind the iterative decoding of 
product codes and  this is applicable no matter the size of these
square product code is or the rectangular product rectangular parity 
check code .
    you iterative method and by this wholes for whether the channel
is BEC  or even BSC ,even for the BSC you would just go row by row ,
and column by column 
    in exactly the same mananer it's shown here, and wherever the parity is not 
satisfied you would flip the corresponding bit. for the BSC maybe you may
do little better by flipping only those bits which when you flip the bit certainly/
more than one parity gets corrected .
    for example if a particular bit is flipped, if the row and column parity both 
get satisfied then you would flip that correspinding bit,but otherwise in fact you 
can still use the same approach even the simpler approach with it ,which 
is shown here . those of you who are proactive would take this particular diagram on
this particular slide side 52 and you implement this in MATLAB. it shouldn't take you 
too much time to implement this paricular encoding and decoing algorithm
    you just give exaclty the same result pattern which is shown here and see 
whether your iterative decoding can go through the same sequence of steps
and recover the transmitted message in the manner that is shown here .  
        obviously this is not part of the project or it's up to you if you want to 
do it or not, but i mean  your 11th and 12th grade physics or chemistry  or 
mathmatics there will not be any examples from NCER Book or any of the other books
    that you may have made use of but it's more like you have to do this work on your
own.develop the programs on your owen which is probably not something that 
you would have done until your school . so this is a great programming exercise it.
     it will allow you to flex your programming muscles and also it will give you a good 
handle on what this iteratvie method is .
      now to move on we are goging to consider the exact same iteratvie decoding but 
in a little more formalized manner in a manner which allows this iterative scheme
to work on codes which are not even this product codes or the rectangular parity 
check codes.
       the underlying idea remains exactly the same but we are going to threat it little
more mathmatically, and that is going to allow us some formalized manner and some additional 
power.that we simply don't have otherwise,
       and so towards that we are going to take a look  at the parity check matrix for 
this (9,4)product code and that as you may have studied from the last set of lecture  notes
. it looks like this the parity check matrix is given by H.
       where H has in this case it has five rows and nine columns.
  why does it have five rows, you can see that HS5 rows the reason it has five rows 
is because there are five parity check equations in the product code ,
two here ,and this additional parity check is the parity .on parity .
all of these five parity check equations have to be satisfied by all of this 9
transmitted bits of the code and when i say they have to be satisfied, what I 
mean is that the product of each of the row of H matrix with the codeword has 
to be 0.
      what are the entries of this H matrix ,the first row corresponds to the first
parity check .
       as you see the first parity check is taking these two message bits and 
introducing this parity bit which is codeword number bit three.
 so that's why there are three months and the rest of of them ,rest of the 
entries in the first rows fist two are zero .similaryly the second row is the 
second row of this square table.as C4 C5  C6  and there's y  c4 c5 c6  I 
have one here . the third row has c1 c4 and c7 this three bits become the 
part of spc and so tha't why i have one here in  c1 c4 and c7  and see cell so 
that is how we have constructed this parity check matrix now we are goging to 
represent this matrix itself  as a graph ,and the top of the graph  is called 
check nodes, we  also called them supervisory nodes and the bottom of the graph 
is nothing but our transmitted codeword bits  in this case C1 to C9  and 
  they are also known as either bit nodes or variable nodes. and this type of 
graph is called the Tanner graph. by the name of the scientists who came up with 
this particular scheme his name is Michael Tanner you can search for Tanner
graph codes online, and you will find the original paper that was written by 
Tanner in 1980s.and it's also called in the graph theory the mathematical branch
of graph theory, this type of graphs are called bipartite graphs and the reason 
they're called bipartite graphs is because all the nodes of this graph 9 plus 5, 
14 note 14 nodes , they formed to clear groups in this case the check nodes and the 
variable nodes. and none of the nodes in one group are connected to the nodes in the same 
group.
      you see that s1 ,s2 ,s3 ,s4,s5, have no interconnections ,between them in same 
where all the variable nodes are also not connected to each other.
this is the graphical representation of the parity check matrix of the (9,4) product 
code ,but it shouldn't be completely a new representation for you because we have 
already done this in the context of single parity check code and also for the 
Hamming code .
       so let's just take a brief look at it . you recall when studied the 
Hamming code we have the same type of graphical representation which is shown here but 
in this case there is only one check node because it's just single parity check code and 
these are the variable nodes.
   let us see a Hamming code .
   Tanner graph for the Hamming code is over here ,these are the three check nodes 
corresponding to 3 parity check equations of the Hamming code and  the 
variable nodes and this is the bipartite graph of the ending code , so in fact 
any linear block code ,once you know it's a parity check matrix here .
      can be converted into a  graphical code .a bipartite graph cool as it's shown here********************这块
so this example is only for the ninth row product code, but the same type of Tanner graph
can be drawn for any linear block code given the H matrix the parity check matrix now
we are going to take that iterative algorithm that we studied in the prior set of
slides and apply to this graphical representation of the product code and so towards that
what we are going to do is we are goging to take the bits that are coming out of the channel
it can be BEC it can be Bsc or AWGN,the method is generally applicable ,we are going to 
load the variable nodes with the output of the channel.
   then we are going to send messagees back and forth . the first V[i] will send the 
message to C[j] and then after that C[j] ends will send the message to  V[i] and then we are
going to iterate over these two steps , and therefore this algorithm is 
called message passing algorithm.
   and there is a whole class of methods that fall under this general terminology 
called message passing .  it's a very powerful approach .
   it's almost getting into the advanced estimation technique but we get a pretty 
good idea of this advanced message passing method by taking this example of 
the product code that we had just looked  at so how does the message message 
passing words work in the first step of message passing all V ends send message 
to the C. NOW remember C is the supervisor node  .so v sends a message 
to it's supervisory node(11:02) and what the V nodes does is, in case of binary 
is as this channel , or by the way , i think i forgot to define what there is 
some terminology called DC& DV.
   DC is the degree of check node,
   DV is called the the degree of variable. and the degree is nothing but degree
of node is nothing but the number of edges that a connected to a particular node.
so degree of this check node is 3 because there are 3 edges that are connected 
to this check node . in fact ,each of these check nodes has the same degree
of three. so DC degree of check nodes for the product code is three .
   DV is the degree of variable node ,for example , DV force the first variable node 
is two , second variable node it's also two. third variable node it's also two .
fourth variable node has a DV value of three.so that is the terminology for DC and DV
. the way i_th VN will send the message to CN  if if DV minus one messages from these 
CN other than the one that the VN is sending the message to if they all are IRA's THEN 
only the VN will send a result to CM. otherwise the VN will just send even if  there is 
one non erasure message from any of the CNS or from the channel  then 
the VN will send that with you .
    this holds for all the iterations except the first one.
where the Vn simply sends the value that it has received this unknown areas value it sends
that if it receives erased value it sends that . now we come to the CN and two VMs message-passing
.here if any to  the DC messages that a paricular CN receives from all the vns that 
are connected to it if all of them are not erased which is this part.when none of the Dv minus one
messages are analysed this particulary. CN will send to this Vn the modular to some of 
those Uh  nearest messages however if even one of the DC minus one message is erased, then 
the CN cannot do anything it will just send illusive .
   and one note is that the paricular node never  sends back a message , which depends on the message
that come from that node itself , because to do so would mean that we are doing postive 
feedback which not a desired thing .if you think of this message passing as if let's 
say you are exhanging rumors that is actually what is going on  each node is kind of 
exchanging rumor about what the value of that particular node is as it hears 
from the other nodes that are connected to it ,now when you exchange rumors.
    suppose you want to pass the rumor to your friend.it's better that you 
don't tell that friend something that actually came from him in the first place,
beacuse then what is the use you actually hear rumors coming from other frieds 
and from that you make your own judgment and give you that to the friend ,thant you are 
sending that particular rumor message so , so that is this entire idea about not creating 
a positive feedback .this may seem a little condensed to you ,right now but when 
we take an example. you wil see that it's fairly straightforward, actually it's the same 
thing that we did earlier in context of row and column decoding . but we are doding 
that now in the context of the steno grapher. this is the Tanner graph of our 
ninth floor product code ,and I have already loaded the variable nodes
with the result bits remember there are five bits which are erased.
    exactly those  five bits are erased here ,also now that row by row
and column decoding that we had done earlier we are going to do same thing 
but we are going to think about it as if there are messagees getting 
exchanged between V ends and  C ends.so let us condider for example in 
the very first case let us condier this particular  CN.
     in the very first step ,all the v ends will send their to the CN so 
,the CN will get [e,1,0], now this CN has to worry about only this e
from this VN , and this CN will send a message back to this VN.
which is a modular to sum of 1 .what is shown here.
   the green lines are the mesage is going from VN to CN
 the blue line is message going from CN back to the Vn.
 the same thing is done by CN number 3.
 that we just said , we discussed and now ,similar situation can 
occurs also at CN number 5.and that is the end of the iteration 
number one all.all the v nodes have send their message to CN .
and CN ends have sent their message back to the V nodes, and 
now you can see that actually three out of five erasers have been
corrected,now we agian ,do the same iteration where again,all 
the V ends will send their  messagees back to the C ends and 

now C ends are able to correct the remaining two users also 
this is the same exact iterative  algorithm except that it has beem
implemented on the Tanner graph.so let us stop here and we will take up
the remaining part in the last set .of slieds.