Real-Time Rendering-第四章 Transforms（2）

4.2 Special Matrix Transforms and Operations

在这一节，将会介绍并推导出在实时图形中大量必不可少的矩阵变换和操作。首先，我们给出了Euler transform（欧拉变换，以及从中提取的参数），这一种描述物体朝向的直观表示方法。然后，我们会涉及到从单个矩阵中获取一组基本变换。最后，推导出一种围绕任意轴旋转一个实体的方法。

4.2.1 The Euler Transform

这是一种直观的变换方法，通过构造一个矩阵来确定你自己（即相机）或任意其他实体在某个特定方向的朝向。该变换的名称源自伟大的瑞士数学家Leonhard Euler（1707-1783）。

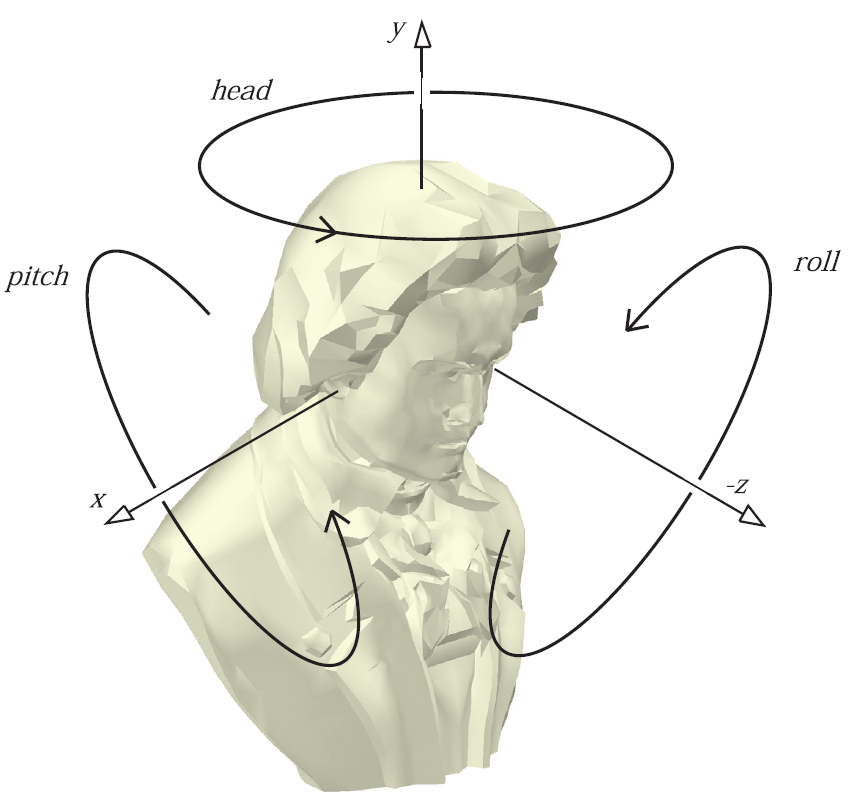
图4.6 根据欧拉变换描述了转动头部，俯仰，翻转的方式。其中默认的观察方向被定义为，沿着负 $z$-轴向前看同时头部沿着 $y$-轴向上。

首先，需要确定某种类型的默认观察方向。通常情况下，沿着负 $z$-轴为观察方向，沿着 $y$-轴为头部向上的方向，如图4.6所示。欧拉变换表示为三个矩阵的乘法运算，这三个旋转矩阵的名称如图所示。公式4.17给出了变换矩阵 $\mathbf{E}$ 的更正式的定义：

$$\mathbf{E}(h,p,r)=\mathbf{R}_z(r)\mathbf{R}_x(p)\mathbf{R}_y(h). \qquad\qquad\qquad\qquad\text{(4.17)}$$

由于矩阵 $\mathbf{E}$ 是一序列旋转矩阵的串联，显然也是正交矩阵。因此，$\mathbf{E}$ 的逆矩阵可以表示为$\mathbf{E}^{-1}=\mathbf{E}^T=(\mathbf{R}_z\mathbf{R}_x\mathbf{R}_y)^T=\mathbf{R}_y^T\mathbf{R}_x^T\mathbf{R}_z^T$，当然，直接使用 $\mathbf{E}$ 的转置更容易。

注：矩阵的顺序实际上有24种不同的选择[1179]，我们之所以使用这种选择是因为这是最常用的一种。

其中欧拉角度 $h$，$p$ 和 $r$ 表示head，pitch和roll分别围绕各自坐标轴旋转的顺序和弧度大小。这种变换是非常直观的，因此很容易使用普通人的语言进行讨论。例如，改变 head 角度使观察者摇头说“不”，改变 pitch 使其点头，改变 roll 则使其把头向两边倾斜。在这里我们讨论的是改变 head，ptich和roll 角度，而不是有关如何围绕 $x$，$y$，和 $z$-轴旋转。需要注意的是，这种变换不仅可以确定相机的方位，还可以用于确定任意对象或实体的方位。可以使用world space的全局坐标轴或相对于本地的参照系执行这些变换。

注：有时把这三个角度都称为“rolls”，比如，把“head”称为“$y$-roll”（绕$y$-轴旋转），“pitch”称为“$x$-roll”（绕$x$-轴旋转）。另外，“head”又可以称为“yaw”（偏航），比如飞行模拟。

当你使用Euler变换时，可以会发生一种称为gimbal lock（万向节锁）的情形[1176，1330]。当旋转过程中失去了一个角度的自由度时就会发生这种情况。比如，假设变换的顺序为 $x/y/z$，仅在第二次旋转操作时，围绕 $y$-轴旋转$\pi/2$。 执行该操作会把本地坐标系的 $z$-轴旋转到与原始的 $x$-轴对齐，因此最后绕 $z$ 轴旋转的操作是多余的。

另一种演示失去其中一个角度的自由度的方法是设置 $p=\pi/2$，并检查Euler矩阵 $\mathbf{E}(h,p,r)$所发生的变换：

$$\begin{aligned} \mathbf{E}(h,\pi/2,r) \quad & = \begin{pmatrix} \cos r\cos h-\sin r\sin h & 0 & \cos r\sin h+\sin r\cos h \\ \sin r\cos h+\cos r\sin h & 0 & \sin r\sin h-\cos r\cos h \\ 0 & 1 & 0 \end{pmatrix} \\ &= \begin{pmatrix} \cos (r+h) & 0 & \sin (r+h) \\ \sin (r+h) & 0 & -\cos (r+h) \\ 0 & 1 & 0 \end{pmatrix}. \qquad\qquad\qquad\qquad\text{(4.18)} \end{aligned}$$

由于该矩阵只依赖于一个角度$(r+h)$，因此我们可以推断其中一个角度的自由度丢失了。

虽然在建模系统中，Euler角度通常被描述为以 $x/y/z$ 的顺序围绕每一个本地坐标轴旋转，但是其他的顺序也是可行的。比如，$z/x/y$ 的顺序用于动画旋转，$z/x/z$ 同时用于动画旋转和物体旋转。所有的旋转顺序都是指定三个独立旋转操作的有效方法。最后一种旋转顺序，$z/x/z$ 在某种应用程序中会更适用，比如当围绕 $x$ 旋转 $\pi$ 弧度（半旋转）出现gimbal lock情形时。也就是说，根据“hairy ball theorem”（毛球定理）万向节锁是无法避免的，没有一个完美的旋转序列能避免出现这种情况。

虽然Euler角度在计算较小角度的变化或观察方向是很实用，但是却有一些其他的严重的局限性。Euler角度无法在两组Euler角度组合的情况下执行。例如，在两个Euler角度之间执行插值，并不是简单的对每一个角度进行插值。实际情况中，两组不同的欧拉角度肯定得到相同的方向，因此任何插值都不应该旋转对象。这些是使用其他的表示替代的部分理由，比如在本章的后面将会讨论的四元数，是值得追求的。

4.2.2 Extracting Parameters from the Euler Transform

在某些情况下，从一个正交矩阵中提取出Euler参数 $h$，$p$ 和 $r$ 的过程是很实用的。这种提取过程如公式4.19所示：

$$\qquad\begin{aligned} \mathbf{F} = \begin{pmatrix} f_{00} & f_{01} & f_{02} \\ f_{10} & f_{11} & f_{12} \\ f_{20} & f_{21} & f_{22} \end{pmatrix} = \mathbf{R}_z(r)\mathbf{R}_x(p)\mathbf{R}_y(h) = \mathbf{E}(h,p,r). \qquad\text{(4.19)} \end{aligned}$$

使用公式4.19把这三个旋转矩阵串联起来得到

$$\begin{aligned} \mathbf{F} = \begin{pmatrix} \cos r\cos h-\sin r\sin p\sin h & -\sin r\cos p & \cos r\sin h+\sin r\sin p\cos h \\ \sin r\cos h+\cos r\sin p\sin h & \cos r\cos p & \sin r\sin h-\cos r\sin p\cos h \\ -\cos p\sin h & \sin p & \cos p\cos h \end{pmatrix}. \qquad\text{(4.20)} \end{aligned}$$

从该公式中可以明显地看出参数 pitch 可以由 $\sin p=f_{21}$ 得到。另外，通过 $f_{01}$ 除以 $f_{11}$，以及 $f_{20}$ 除以 $f_{22}$，可以得到以下获取参数 head和 roll 的计算公式：

$$\qquad\qquad\begin{aligned} \frac{f_{01}}{f_{11}} &= \frac{-\sin r}{\cos r} = -\tan r,\\ \frac{f_{20}}{f_{22}} &= \frac{-\sin h}{\cos h} = -\tan h. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.21)}$$

因此，使用公式4.22所示的函数 $\mathrm{atan2(y,x)}$（见第1章）可以从矩阵 $\mathbf{F}$ 中提取出欧拉参数 $h$（head)，$p$（pitch）和 $r$（roll）。

$$\qquad\qquad\begin{aligned} h\ &= \mathrm{atan2}(-f_{20},f_{22}),\\ p\ &= \arcsin(f_{21}),\\ r\ &= \mathrm{atan2}(-f_{01},f_{11}). \end{aligned} \qquad\qquad\qquad\qquad \text{(4.22)}$$

然而，我们还需要处理一种特殊的情况，当 $\cos p=0$的情况，因为此时$f_{01}=f_{11}=0$，所以不能使用 $\mathrm{atan2}$ 函数。当 $\cos p=0$时，则有$\sin p=\pm1$，因此 $\mathbf{F}$可以简化为

$$\begin{aligned} \mathbf{F} = \begin{pmatrix} \cos(r\pm h) & 0 & \sin(r\pm h) \\ \sin(r\pm h) & 0 & -\cos(r\pm h) \\ 0 & \pm1 & 0 \end{pmatrix}. \qquad\qquad\text{(4.23)} \end{aligned}$$

另外两个参数的获取方法是，首先设置 $h=0$[1265]，然后由 $\sin r/ \cos r=\tan r=f_{10}/f_{00}$得到 $r=\mathrm{atan2}(f_{00},f_{10})$。

需要注意的是从三角函数 $\arcsin$（见附录B.1节）的定义域 $-\pi/2\leq p \leq \pi/2$，可以得知如果用于创建矩阵 $\mathbf{F}$ 的参数 $p$ 位于该范围之外，则无法从 $\mathbf{F}$ 中提取出原始的参数值。另外参数 $h$，$p$，和 $r$ 的值并不是唯一的，也就是说不止有一组欧拉参数可以用于产生同样的变换矩阵。更多关于欧拉角度转换的内容可以查看Shoemake在1994年发表的文章[1179]。以上概述的简单方法会导致数值不稳定的问题，但是通过增加计算成本就可以避免。

EXAMPLE: CONSTRAINING A TRANSFORM（约束变换）。想象一下你正握着一把夹着螺栓的扳手，要把螺栓拧到正确的位置你需要围绕 $x$-轴旋转扳手。现在假设你所使用的输入设备（鼠标，VR手套，空间球等等）会给出一个用于移动扳手的正交变换矩阵。此时面对的问题是，你并不想使用该变换矩阵操作扳手，因为扳手只能绕着 $x$-轴旋转。因此需要把设备输入的变换矩阵 $\mathbf{P}$ 限制为围绕 $x$-轴旋转，使用本节所讨论的方法从矩阵 $\mathbf{P}$ 中提取出欧拉角度 $h$，$p$，和 $r$，然后创建一个新的矩阵 $\mathbf{R}_x(p)$。该矩阵就是围绕 $x$-轴旋转扳手所需要的变换矩阵（如果 $\mathbf{P}$ 中包含了该移动操作）。

4.2.3 Matrix Decomposition

到目前为止，我们所做的工作都是在假设我们知道所使用的变换矩阵的起源和历史的情况下进行的。这并不是常见的情况：例如，通常与变换后的对象关联的只不过是一个串联矩阵。从一个串联矩阵中取出多个变换矩阵的工作称为matrix decompostion（矩阵分解）。

从一个串联矩阵中取出一组变换矩阵有多种理由。包括：

• 提取某个对象的缩放比例因子。
• 查找特定系统需要的变换矩阵。例如，VRML（Virtual Reality Modeling Language） [1310] 使用了一种Transform（变换）节点（见4.1.5 节）并且不允许使用任意的 $4\times4$ 矩阵。
• 确定一个模型是否只经过了刚体变换操作。
• 在一个动画的两个关键帧之间进行插值运算时，只有该动画对象使用的矩阵是可用的。
• 从一个旋转矩阵中去掉切变矩阵。

在前面我们已经提出了两种分解，第一种是从刚体变换矩阵（见4.1.6节）中推导出平移和旋转矩阵，第二种是从正交矩阵中提取出欧拉角度（见4.2.2节）。

正如我们前面所看到的，获取平移矩阵是微不足道的，只需要简单地得到 $4\times4$矩阵的最后一列。我们也可以通过检查矩阵的行列式是否为0，确定是否产生了反射矩阵。要分离出旋转，缩放以及切变矩阵则需要更坚定的努力。

幸运的是，关于该主题有大量的文章，以及可用的在线代码。Thomas[1265]和Goldman[414，415]分别提出了获取各种变换矩阵的略微不同的方法。Shoemake[1178]改进了仿射矩阵的技术，他所使用的算法独立于参考框架，并试图分解矩阵从而获得刚体变换。

4.2.4 Rotation about an Arbitrary Axis

有时通过一些步骤可以方便地把实体围绕任意轴旋转一定的角度。假设旋转轴 $\mathbf{r}$ 已经规范化，需要创建一个围绕 $\mathbf{r}$ 旋转 $\alpha$ 弧度的变换矩阵。

要创建该变换矩阵，首先找出两个相互正交的单位长度的任意轴，并且与 $\mathbf{r}$ 正交，即这三个轴构成标准正交。形成了一个标准正交基。实现思想是把基（见附录A.3.2节）由标准基改变为这个新的正交基，然后围绕 $x$-轴（该轴现在对应于 $\mathbf{r}$）旋转 $\alpha$ 弧度，最后再变换回标准基。该变换过程如图4.7所示。

注：关于向量基的一个例子是标准基，对应的轴分别为 $\mathbf{e}_x=(1,0,0)$，$\mathbf{e}_y=(0,1,0)$，$\mathbf{e}_z=(0,0,1)$。

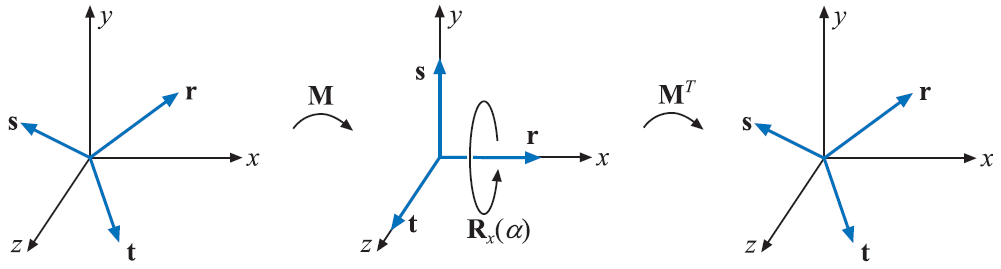
图4.7 绕任意轴 $\mathbf{r}$ 旋转，通过找出一个由 $\mathbf{r}$，$\mathbf{s}$，$\mathbf{t}$形成的标准正交基实现。然后把该正交基与标准基对齐，使得 $\mathbf{r}$ 与 $x$-轴对齐。在该正交基上绕 $x$-轴进行旋转，最后变换回标准基。

第一步是计算标准正交基的轴向量。第一个轴是 $\mathbf{r}$，即我们要围绕此进行旋转的轴。接下来集中找出第二个轴 $\mathbf{s}$ ，就可以根据第一个轴和第二个轴的叉积得到第三个轴向量 $\mathbf{t}=\mathbf{r}\times\mathbf{s}$。一种数据稳定的方法是找出 $\mathbf{r}$中最小的分量值（绝对值），并把该分量设为0。然后交换另外两个分量，并把第一个分量值取反。这个过程在数学上表示为[576]：

$$\qquad\qquad\begin{aligned} \bar{\mathbf{s}} &= \begin{cases} (0,-r_z,r_y), & \text{如果 $|r_x|<|r_y|$ 并且 $|r_x|<|r_z|$}, \\ (-r_z,0,r_x), & \text{如果 $|r_y|<|r_x|$ 并且 $|r_y|<|r_z|$}, \\ (-r_y,r_x,0), & \text{如果 $|r_z|<|r_x|$ 并且 $|r_z|<|r_y|$}, \end{cases} \\ \mathbf{s} &= \bar{\mathbf{s}}/\|\bar{\mathbf{s}}\|, \\ \mathbf{t} &= \mathbf{r} \times \mathbf{s}. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.24)}$$

注：实际上可以对两个分量中的任意一个非0分量值取反。

这保证了向量 $\mathbf{s}$ 正交于（垂直） $\mathbf{r}$，并且$(\mathbf{r,s,t})$是一个标准正交基。我们可以使用如下的方式把这三个向量作为矩阵的行向量：

$$\begin{aligned} \mathbf{F} = \begin{pmatrix} \mathbf{r}^T \\ \mathbf{s}^T \\ \mathbf{t}^T \end{pmatrix}. \qquad\qquad\text{(4.25)} \end{aligned}$$

该矩阵把向量 $\mathbf{r}$ 变换到 $x$-轴（标准基$\mathbf{e}_x$），把 $\mathbf{s}$ 变换到 $y$-轴，$\mathbf{t}$ 变换到 $z$-轴。然后就可以得到围绕规范化的向量 $\mathbf{r}$ 旋转 $\alpha$ 弧度的最终变换矩阵为：

$$\mathbf{X}=\mathbf{M}^T\mathbf{R}_x(\alpha)\mathbf{M}. \qquad\qquad\qquad\qquad\text{(4.26)}$$

换句话说，该过程意味着我们先把基向量 $\mathbf{r}$ 变换为 $x$-轴（使用矩阵$\mathbf{M}$），然后绕着 $x$-轴旋转 $\alpha$ 弧度（使用$\mathbf{R}_x(\alpha)$），最后使用 $\mathbf{M}$ 的逆矩阵再变换回标准基，在这里使用 $\mathbf{M}^T$ 表示逆矩阵，因为 $\mathbf{M}$ 是正交矩阵。

Goldman提出了另一种方法用于围绕一个任意的规范化的向量轴 $\mathbf{r}$ 旋转 $\phi$ 弧度。在这里，我们只是简单列出该变换矩阵：

$$\begin{aligned} \mathbf{R} = \begin{pmatrix} \cos\phi+(1-\cos\phi)r_x^2 & (1-\cos\phi)r_xr_y-r_x\sin\phi & (1-\cos\phi)r_xr_z+r_y\sin\phi \\ (1-\cos\phi)r_xr_y+r_z\sin\phi & \cos\phi+(1-\cos\phi)r_y^2 & (1-\cos\phi)r_yr_z-r_x\sin\phi \\ (1-\cos\phi)r_xr_z-r_y\sin\phi & (1-\cos\phi)r_yr_z+r_x\sin\phi & \cos\phi+(1-\cos\phi)r_z^2 \end{pmatrix}. \qquad\text{(4.27)} \end{aligned}$$

在4.3.2节，我们将会使用四元数给出解决该问题的另一种方法。在该节还会讲解更高效的算法用于解决相关的问题，比如从一个向量旋转到另一个向量。