群论基础速成（6）：五大著名群族

笨牛慢耕

已于 2022-04-24 19:57:28 修改

阅读量5.3k

点赞数 14

分类专栏：数理计科文章标签：群论对称群循环群阿贝尔群二面体群

于 2022-04-24 19:55:36 首次发布

本文链接：https://blog.csdn.net/chenxy_bwave/article/details/122963485

版权

数理计科专栏收录该内容

14 篇文章

订阅专栏

4.2 置换的表示及cyclic notation

0. 前言

业余爱好小白的群论自学笔记。没有目的，为了学习而学习。用自己能够理解的方式沿着自己的思路进行整理记述（东施效颦小平邦彦的抄书学数学），不求严谨完备，但求逻辑连贯。

本篇将全面地浏览介绍一下五个基本而典型的群族：循环群，阿贝尔群，二面体群；对称群和交错群。有些我们在此前已经提及了，但是这里我们将进一步涉及到各种群族之间的关系。

1. 循环群

循环群是最简单的一种群，它只需要一个生成元。但是，循环群并不限于只能由一个生成元生成。正如我们在上一篇中所举的例子，循环群 $C_6$ 也可以由{2,3}两个生成元生成。循环群与整数的模n加法所得到的群 $Z_n$ 同构。有些文献也直接用 $Z_n$ 指称循环群。

循环群属于阿贝尔群（交换群）。它的凯莱表（乘法表，虽然这明明是加法表^-^）具有非常明显的模式：

循环群会出现在所有其它群中，换句话说，任何其它群都包含循环群作为子群。与之相关联的概念是轨道（参见上一篇：群论基础速成（5）），包含单位元的轨道构成一个循环子群。

在现实世界中，循环群用于描述物体的旋转对称。只有旋转对称性的物体的对称性只能用循环群来描述；而除了旋转对称性还包含其它对称性的物体的对称性可以用更复杂的群来描述，但是只考察它的旋转对称性时，则得到了循环群。这对应了以上“任意群都包含循环子群”的论断，这里的循环子群就对应着物体的旋转对称性。如下是两个只有旋转对称性的物体：六叶螺旋桨和八叶风车。

2. 阿贝尔群

阿贝尔群是指群二元运算是可交换的， $a*b=b*a$ 。也称可交换群。

这一特性决定了阿贝尔群中，群运算的顺序不管如何排列得到的结果都相同，比如说有三个元素的群： $abc=acb=bac=bca=cba=cab$

群运算的可交换性决定了阿贝尔群的乘法表是关于对角线对称的。注意，不要混淆这个乘法表的对称性与后面将要说到的对称群，此对称非彼对称。

如上一节所述，循环群是属于阿贝尔群，但是阿贝尔群与循环群的关系并不仅限于此，事实上有以下定理。

2.1 阿贝尔群基本定理

每个有限阿贝尔群都同构于循环群的直积。

2.2 阿贝尔群的可视化判别方法

群运算可交换性决定了在阿贝尔群的凯莱图中，从同一结点出发的每对箭头都应该形成一个闭合的“菱形”。是不是标准的菱形并不重要，重要的是连接的模式。如下图所示：

在阿贝尔群的凯莱图中不会出现左边这种模式，永远都是右边这种模式。

上图所示两个凯莱图非常相近，其区别仅在于内环与外环的方向相同还是相反。用以上方式我们能很容易地辨别左边是非阿贝尔群，而右边是阿贝尔群。

3. 二面体群

与循环群只描述物体的旋转对称性不同，二面体群用于描述旋转对称性与轴对称性的结合。比如说，正多边形就同时具有旋转对称性，和轴对称性。因此正多边形的对称性可以用二面体群进行描述。二面体群通常记为 $D_n$ ，其中D代表Dihedral（二面的；有两个平面的; n. 两面角，二面角）。

3.1 旋转对称性和轴对称性

一个物体如果沿着某个方向以及某个轴线翻转后看起来仍然是原来的样子，就是具有轴对称。

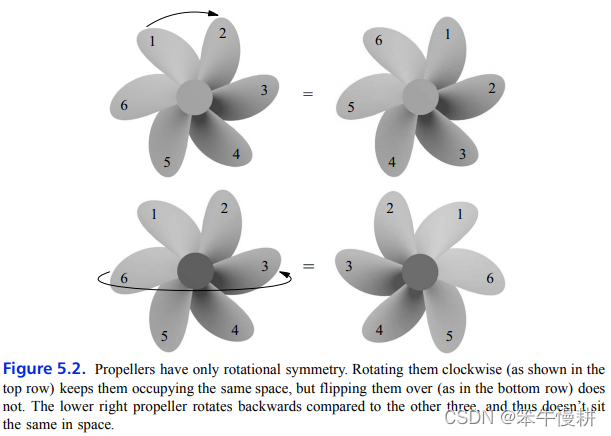
如上图所示，螺旋桨只有旋转对称性，而没有轴对称性。左下的图经过翻转后变成右下的图，显然它所占据的空间有变化。

而正多边形则是同时具有旋转对称性和轴对称性的物体。比如说正方形，它旋转{0,90,180,270}后形状看起来和原来一样，说明它具有旋转对称性。它沿着两条对角线或者两个连接对向边的中点的中线翻转后的形状看起来也和翻转前一样，说明它具有轴对称性。如下图所示为正三角形的情况，同样具有旋转对称性和轴对称性：

3.2 二面体群的凯莱图

如下图所示为 $D_3, D_5, D_n$ 的凯莱图。

它们有着很明显的共同特征：

(1) 由内环和外环构成，外环（当然这里内、外是相对的）代表一个循环群，内环是外环的一个副本，但是它不构成循环群，因为它不包含单位元
(2) 内环与外环的旋转方向相反

为什么它们转的方向相反呢？这是由于翻转所带来的效应。翻转前的顺时针旋转与翻转后的逆时针旋转会得到相同的效果。

二面体群 $D_3$ 与对称群 $S_3$ 同构。但是，这种情况是唯一的。对于任意的n>3， $D_n$ 不会同构于 $S_n$ ,而是（正如下一节会提到的一样）同构于 $S_n$ 的某个子群。 $D_3$ 与对称群 $S_3$ 同构可以认为是一种巧合，它们的元素个数都为 $6 = 3! = 2*3$ 。

3.3 二面体群的乘法表

上图所示为二面体群 $D_5$ 的乘法表，如图所示，可以明显地分为4个区域。

左上代表的外环所代表的子群的凯莱图；
右下对应的是内环，它本身不构成一个子群（乘法表的内环与外环部分的差异如何解释？）；
左下区域是左上区域的对应元素乘以翻转元 $f$ 所得，右上区域是右下区域的对应元素乘以翻转元 $f$ 所得。

从二面体群的凯莱图中可以看出它蕴含了一个2x2的模式，这个模式与2阶群的乘法表一致。这事实上是 $D_n$ 可以由 $C_n$ 与 $C_2$ 的半直积得到是相关联的。

3.4 二面体群的循环图

很明显，二面体群 $D_n$ 的循环图有一个代表它的循环子群 $C_n$ 的 $r$ 的轨道以及若干个2阶轨道（分别对应除 $r$ 以外的各个元素的轨道）。

4. 对称群

引入对称群前首先要介绍置换和置换群。

4.1 置换

所谓置换（permutation）是指对一组有序排列的元素进行顺序重排。比如说[1,3,2]是[1,2,3]的一个置换。置换可以描述牌桌上的洗牌，一个单词中字母的重组，等等。

显而易见的是，含有n个元素的不同排列方式有n的阶乘（ $n!$ ）种。

4.2 置换的表示及cyclic notation

数学家用以表示置换的符号有很多种，一种常见的方式叫做cyclic notation。cyclic notation中用箭头表示元素位置挪动方式，而且是以循环的方式表达。如下所示：

这个表达的置换操作是：将原第1个位置（或者说元素索引）上的元素挪到第2个位置，原第2个位置上的元素挪到第3个位置，原第3个位置上的元素挪到第4个位置，原第4个位置上的元素挪到第1个位置。再看一个例子：

这个表达的置换操作是：将原第3个位置上的元素挪到第4个位置，原第4个位置上的元素挪到第3个位置，以上表示中没有出现1和2，这表示第1个位置和第2个位置的元素保持不动。

这里我们需要搞清楚当我们说（xyz是yxz的一个）置换时，和说置换操作时，两个置换的含义略有不同。当我们说“说[1,3,2]是[1,2,3]的一个置换”，这里的1，2，3是指元素本身，而不是位置，它们的排列方式代表置换操作的结果；而在置换操作中比如说以上置换操作表示中出现的数字指的不是元素值，而是指位置，置换操作整体指的是一个作用。如下图所示：

[u,x,y,z]是[x,y,z,u]经过左边这个置换操作而得的一个置换， [u,x,z,y]是[u,x,y,z]经过右边这个置换而得的一个置换。从[x,y,z,u]经过两次置换操作后得到[u,x,z,y]。

但是，实际上这样的用箭头表示很不容易做文档，所以通常就简写为（以以上两个置换为例）：(1,2,3,4)，(3,4)。注意，在简记法中，只有有箭头对应的才会出现。更多的简记例子参见下面交错群中的例子说明。

注：我在好几本将抽象代数的教科书（包括Artin的Algebra），很奇怪的是，都是一上来就直接用cyclic notation，不做任何前置性说明。我花了很长的时间才真正明白了cyclic notation是怎么回事。所以这里特意稍微啰嗦一下把我自己的理解描述一下^-^。

4.3 置换群

置换符合我们对群的所有要求。置换是一个自然的构造群的工具。

置换群并不是一个正式的群族的名称，而只是说基于置换来构造的群的总称。

4.4 对称群

一个给定集合的所有置换构成的群称为对称群，通常记为 $S_n$ 。

所以，一个具有N个元素的集合，由它的所有置换构成的对称群的元素的个数自然就是N的阶乘 $N!$ 个。

4.5 置换群与对称群的关系

尽管n个元素的所有置换构成对称群，但是，构造一个置换群并不需要一个给定集合的所有置换。一般来说，从 $S_n$ 中选取一部分置换也可能得到一个群。

所以，可以说：对称群是一种特殊的置换群。

从另一个角度，我们也可以说：任何置换群都是对称群的子群。

4.6 凯莱定理

进一步，事实上，任何有限群都同构于某对称群 $S_n$ 的一个子群，或者说任何有限群都同构于一个置换群。

所以，正如4.3中所说的“置换是一个自然的构造群的工具”，任意有限群都可以用置换来构造出来！

如下图所示为 $S_4$ 的凯莱图，右边则是凯莱图中的箭头所表示的置换。如图所示，正方体的八个顶点，每个都扩展为3个节点，所以总共是24个节点，等于4的阶乘。

任何阶数24以内的有限群都是 $S_4$ 的子群（同构于 $S_4$ 的某个子群）。

5. 交错群

如上一节所述，从 $S_n$ 中选取一部分置换也可能得到一个群。

但是并不是任选一部分置换子集都能构成一个群。比如说，你所选的置换子集至少必须包括单位元，才可能构成一个群。

将 $S_n$ 的每个元素取其平方（自乘，或者连续两次相同的作用），得到的集合将是一个元素个数只有 $S_n$ 的一半（换句话说，有一半的元素不能表达为另外的元素的平方），这些元素满足群的条件，由这些元素构成的群被称为交错群，记作 $A_n$ 。以下为由 $S_3$ 生成交错群 $A_3$ 的示例。

左侧为 $S_3$ 的各元素的循环表示（cyclic notation），右侧为各元素的平方。 $S_3$ 中（从上到下）第1个元素简记为( )（空的，表示没有元素位置的调换挪动）; 第2个元素简记为( 1,2)；第3个元素简记为( 2,3)；第4个元素简记为( 1,3)；第5个元素简记为( 1,2,3)；第6个元素简记为( 1,3,2).

以(1,3,2)的平方为例，[x,y,z]经过(1,3,2)置换后得到[y,z,x]，然后[y,z,x]经过(1,3,2)置换后得到[z,x,y]。而从[x,y,z]经过(1,2,3)置换也可以直接得到[z,x,y]，因此说(1,3,2) * (1,3,2) = (1,2,3)。

我们知道，阶数为3的群只有一个结构，所以3阶交错群 $A_3$ 是同构于3阶循环群 $C_3$ 的。

6. 柏拉图立方体

有五种正多面体，分别是：正四面体，立方体，正八面体，正十二面体，正二十面体。

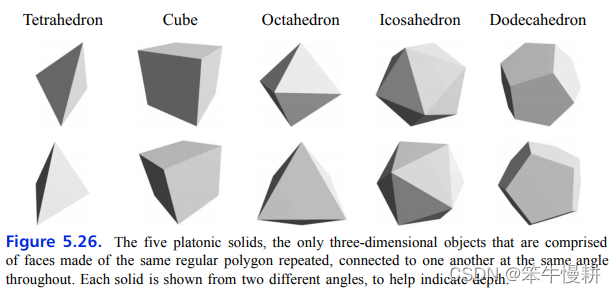
这些正多面体的对称性就分别可以用对称群和交错群来刻画，分别如下：

正四面体： $A_4$
正方体： $S_4$
正八面体： $S_4$
正十二面体： $A_5$
正二十面体： $A_5$

顺便说一下，自然语言尤其固有的含糊之处，因此即便在数学教科书中出现的自然语言描述也会出现让人（特别是初学者）头大的模糊之处。比如说在《群论彩图版》#5.4.3中，有这样的描述：“正四面体的对称群是 $A_4$ ”（其英文原文是“The symmetry group for the tetrahedron is A4”,翻译没毛病）。这句话中的对称群不是上面我们介绍的一个由一个元素集合的所有置换构成的对称群这个群族，而是指“用于描述某某某的对称特性的群”。所以严格一点来说的（由于对称群已经变成了一个专有名词）话应该是：用于描述正字面体的对称特性的群是 $A_4$ ，或者说，可以用 $A_4$ 来描述正四面体的对称特性。

回到本系列总目录：群论基础速成(A crash course for group theory)（1）

参考文献：

内森.卡特著，郭小强罗翠玲译群论彩图版