傅里叶变换

　　傅里叶变换是应用最广泛的数学公式之一，是世界上最伟大的公式。具体应用我就不赘述了，学工科的各位既然来看我的博客，想必都见识过。写这篇博客不仅是我自己对傅里叶变换的一个总结，同时也希望大家看了能够轻松地去学习和研究它。如果内容出现了错误，还望大家批评指正，小弟在此先谢了。

一、欧拉公式

　　欧拉公式是数学基本公式，它将三角函数和指数函数用一种令人难以置信的方式联系了起来。要说明傅里叶变换，就必须提到欧拉公式。
　　学过高中数学的都知道，一个实数可以用一维坐标轴上的一个点来唯一确定，那么一个复数在平面直角坐标轴中怎么唯一确定呢？任意一个复数z可以表示为 $z = a + bj$，其中的a和b都是实数，我们可以分别用横轴和纵轴上的一个点来唯一确定，因此一个复数对应到平面上的一个点。
　　　　　　　　　
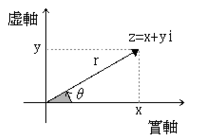
　　我们令上图中的$\theta=x$，$r=1$，通过简单的三角函数知识就可以得到$z=cosx+jsinx$。此时对等号两边分别求导得：
　　　$\frac{dz}{dx}=-sinx+jcosx=j^2sinx+jcosx=j(cosx+jsinx)=jz$
　　分离变量：
　　　　　　　　　　　　　　$\frac{1}{z}dz=jdx$　　　　
　　对两边分别积分：
　　$lnz=jx+C$　
　　为了确定C的值，令 $x=0$ 得到 $C=0$，代入上面的式子得到：
　　$e^{jx}=z=cosx+jsinx$
　　以上就是欧拉公式的证明过程。从这个公式可以得到以下几条信息：
　　1. $e^{jx}$的实部和虚部都是三角函数，从某种意义上来看，它就是一个周期性三角函数，周期和它的实部以及虚部是一致的。
　　2. $e^{jx}$的模长为1，因为$(sinx)^2+(cosx)^2=1$。
　　3. $e^{jx}$ 是一个正交函数，这一点很重要，我会在下面说明。
　　　　

二、傅里叶级数

　　傅里叶级数是傅里叶变换的基础，所以我们从它入手，最后将它推广为傅里叶变换。

1. 正交基观点
   　　任何一个n维向量都可以由一组n维正交基的线性组合确定，这样做有一个好处就是在实际解决问题的时候，我们只要关注这些基底的系数，而不用关心这些基底。举个简单的例子，在平面直角坐标系中，所有的向量都由横轴和纵轴上的单位向量线性组合得到，所以在我们的学习过程中，从来没有用到这两个基底，而是用到它们的系数x和y，从而大大简化了使用的细节和步骤。
   　　从另一个角度来看，对不同的基底，同一个向量的表示都是不同的，但是实际上它们是同一个向量，这是不是有了一丝哲学的意味。如果要扯哲学的话，正交基甚至可以看做一对矛盾，哈哈。我们平常在生活中看待一件事，着眼的角度不同，看法也会不同，映射到正交基上，正交基就可以看做是所谓的“角度”或者“空间”，每一组不同的正交基都唯一决定了一个“空间”，在这个空间里，正交基就是唯一的“法则”。所以，我们可以认为在我们所处的世界之外还有无数个世界，这些世界里也存在一个“你”，但是这个“你”不再服从你熟悉的规则，而是服从那个世界的规则，是不是越看越玄乎了？其实这不是我乱说的，科学界称这些“世界”为“域”，以时间为规则的域叫做时域，以空间为规则的域称为空间域，以频率为规则的域就是傅里叶变换提到的频域。我们在时域中，经历着生老病死，数着时间过日子，但是在频域里，我们的存在早已被注定，你细致苛刻规划的未来，根本就是一个必定的终点，所以在频域内，时间失去了作为度量的意义，取而代之的是频率。那样一个永恒不变的世界，你觉得纯粹是想象，但是你怎么知道在频域里的“你”看来，时域不是一个想象的世界呢？傅里叶经过深入的研究，归纳了频域这个世界的法则，从而揭示了频域的神秘面纱。这个法则就是复指数正交函数。
   　　正交函数和正交基的思想是一致的，也就是说，一组正交函数的线性组合可以唯一确定一个函数。严谨的证明是由最小化均方误差出发，我这里就不搞得那么复杂，给大家提供一个比较好理解的证明思路。
   　　正交向量大家都清楚，两个向量的内积为零，它们就是正交的。例如两个n维的向量（$a_1,a_2,a_3,...,a_n$）和（$b_1,b_2,b_3,...,b_n$）正交，那么$a_1b_1+a_2b_2+a_3b_3+...+a_nb_n=0$。现在我们要明白这个n到底代表什么？平常说的n维是什么意思？如果一个向量只有一维，那么它只有一个元素，只能表示实轴上的一个点，这个点所处的空间是一维的；如果向量是二维的，那么它有两个元素，可以表示平面上的一个点，这个点所处的空间是二维的。所以n维就代表了向量的元素个数，也代表了向量所处的空间维度。
   　　那么一个函数的维度该怎么确定呢？向量是元素的有序集合，所以向量的维度以元素的个数决定，类比一下，函数的元素是什么？显然是点而不是数，所以点的个数决定了函数的维度。问：一个连续的函数有多少个点？答：无穷多个。所以连续函数的维度是无穷的。
   　　既然函数维度是无穷的，那么意味着我们在进行内积的时候的求和项是无穷的，求和就变成了积分。但是仅仅这样定义对实函数是成立了，但是要拓展到复函数还是不行，要对其中一个函数做共轭来消除$j$ 的影响。
   　　因为目前的信号只研究时域和频域，时域的法则大家都明白，以时间为刻度，所以我们就给出其他域（重点是频域）的正交函数定义：
   　　如果集合{$\psi_0,\psi_1,\psi_2,...,\psi_N$}中各个函数满足：
   　　$\int_{t_1}^{t_2}\psi_n(t)\psi_{m}^{*}(t)dt=\left\{\begin{array}{ll}0&\text{$n\ne m$}\\k&\text{$n=m$}.\end{array}\right.$
   　　则{$\psi_n(t)$}为正交函数集。
   　　频域的正交函数集就是复指数正交函数集{$e^{jnw_0t}$}。为什么说它是正交的呢？我们用定义来证明一下。
   　　根据欧拉公式 $e^{jnw_0t}=cos(nw_0t)+jsin(nw_0t)$，显然$e^{jnw_0t}$ 是一个周期函数，周期为$\frac{2\pi}{nw_0}$，当$n=1$时，取最大周期$\frac{2\pi}{w_0}$。既然是一个周期函数，我们只要关注该函数一个周期的行为即可，所以积分的上下限之差可为一个周期。对不同的n有不同的周期，所以我们干脆取函数集的最大周期$\frac{2\pi}{w_0}$ 为周期$T_0$。
   　　$\int_{t_1}^{t_1+T_0}e^{jnw_0t}e^{-jmw_0t}dt$=$\int_{t_1}^{t_1+T_0}e^{j(n-m)w_0t}dt$
   　　当$n=m$时，$e^{j(n-m)w_0t}=1$，所以积分为$T_0$;
   　　当$n\ne m$时，
   $\int_{t_1}^{t_1+T_0}e^{j(n-m)w_0t}dt=\frac{1}{j(n-m)w_0}[e^{j(n-m)w_0(t_1+T_0)}-e^{j(n-m)w_0t_1}]=\frac{e^{j(n-m)w_0t_1}}{j(n-m)w_0}[e^{j(n-m)w_0T_0}-1]=\frac{e^{j(n-m)w_0t_1}}{j(n-m)w_0}[e^{j(n-m)2\pi}-1]=0$
   　　可见，复指数函数集是正交函数集，且正交的基点或者度量是$nw_0$，也就是一系列频率或者周期（谐波），因此，这个由复指数函数集确定的域就被称为频域。
   　　既然我们已经找到了频域的一组基函数，那么根据基函数的定义，对一个连续的函数，我们可以用这组基来得到它的频域表示，这个“表达方式”就是我们耳熟能详的“傅里叶级数”了。但是要注意，复指数函数集的所有函数都是周期函数，所以我们用它作为基来表示的也是一个周期函数。
   　　由此得到一个周期信号的傅里叶级数表示：
   　　$x(t)=\sum_{k=- \infty}^{+ \infty}a_ke^{jkw_0t}$
   　　问题在于$a_k$作为这些复指数基底的权，要怎么确定？我们知道，一个向量要得到某个基的权，只要将这个向量和这个基做内积就可以了，同样的，要得到$a_{k'}$的值，我们同样可以和 $a_{k'}$对应的基 $e^{jk'w_0t}$做内积。下面的论证过程看起来很繁琐，但是其实不复杂。
   　　内积要消除时间$t$的影响，所以要对时间域做积分。
   　　$a_{k'}=\int_{-\infty}^{+\infty}x(t)e^{jk'w_0t}dt=\int_{-\infty}^{+\infty}(\sum_{k=- \infty}^{+ \infty}a_ke^{jkw_0t})e^{jk'w_0t}dt$
   　　交换积分和求和顺序得：
   　　$\sum_{k=- \infty}^{+ \infty}a_k(\int_{-\infty}^{+\infty}e^{jkw_0t}e^{jk'w_0t}dt)=\sum_{k=- \infty}^{+ \infty}a_k(\int_{-\infty}^{+\infty}e^{j(k+k')w_0t}dt)$
   　　单独看括号内的一项：$\int_{-\infty}^{+\infty}e^{j(k+k')w_0t}dt$，由欧拉公式我们知道复指数函数是周期函数。如果$k\ne-k'$那么 $e^{j(k+k')w_0t}$就是一个周期函数（正弦），我们知道正弦函数一个周期的时域积分为0，因此将时间拓展到无穷，依然积分为0；如果$k=-k'$，那么 $e^{j(k+k')w_0t}=1$，无穷积分就是无限大。所以得到下面这个结论：
   　　$\int_{-\infty}^{+\infty}e^{j(k+k')w_0t}dt=\left\{\begin{array}{ll}0&\text{$k\ne -k'$}\\\infty&\text{$k=-k'$}.\end{array}\right.$
   　　如果看官知道单位冲激函数的话，上面的公式也可以表示成：
   　　$\int_{-\infty}^{+\infty}e^{j(k+k')w_0t}dt=\delta(k+k')$
   　　再把这个结论代回原来的公式中：
   　　$\int_{-\infty}^{+\infty}x(t)e^{jk'w_0t}dt=\sum_{k=- \infty}^{+ \infty}a_k(\int_{-\infty}^{+\infty}e^{j(k+k')w_0t}dt)=\sum_{k=- \infty}^{+ \infty}[a_k\delta(k+k')]=\infty a_{-k'}$
   　　得到$a_k$的最终形式：
   　　$a_k=\frac{1}{\infty}\int_{-\infty}^{+\infty}x(t)e^{-jkw_0t}dt$
   　　因为无穷符号不好看，我们通常取$x(t)$的一个周期进行积分得到$a_k$:
   　　$a_k=\frac{1}{T}\int_{T}x(t)e^{-jkw_0t}dt$
   　　这样，我们就从正交基的观点解释了傅里叶级数的整个推导过程。应该还是蛮浅显易懂的吧哈哈哈，其实看官如果只是想理解傅里叶变换的话，就没有必要看我上面打的那些公式，直接看文字解释就好。