图论（12）超哈密尔顿图与超可迹图

最新推荐文章于 2024-05-24 20:20:13 发布
最新推荐文章于 2024-05-24 20:20:13 发布
阅读量3.3k 收藏 3
点赞数
分类专栏： 图论
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/chk_plusplus/article/details/105915106
版权

目录

一、超H图与超H迹

超H图

超可迹图

关于H图的一些猜想

二、E图与H图的关系

线图概念

线图性质

从线图的角度考虑欧拉图与哈密尔顿图关系（考试不作要求）

一、超H图与超H迹

超H图

彼得森图是3正则图，每个顶点关联的有3条边，假设彼得森图是H图的话，则存在H圈，且每个顶点都有两条边在H圈中，因为H圈要包括每一个顶点，但只能有2条边在H圈中，还有1条边不在圈中，因为每个顶点只能走一次。而且H圈中肯定不能存在更小的圈

证明彼得森图是超H图，要证两点，（1）彼得森图是非H图，（2）去掉任意一个顶点后是H图

这里前边的性质定理判定定理之类的都不能用，只能用逻辑推理

这里用反证法，假设彼得森图是H图，忽略下图中若不然三个字，，，

 

部分红色边构成了一个小圈，所以这种情况下不符合假设

形成小圈，与假设不符

综上，假设彼得森图是H图的假设不成立，即彼得森图不是H图。

 

所以得到，彼得森图是超哈密尔顿图。

超可迹图

证明就算了，真的不想看

关于H图的一些猜想

平方图点集不变，若在原图中两个点距离小于等于2，则在平方图中把两个点相连

上边定理仅作了解

二、E图与H图的关系

线图概念

即把原图中的边映射成点，且如果在原图中边邻接，则在线图中对应两个点相连

迭线图就是做多次线图

线图性质

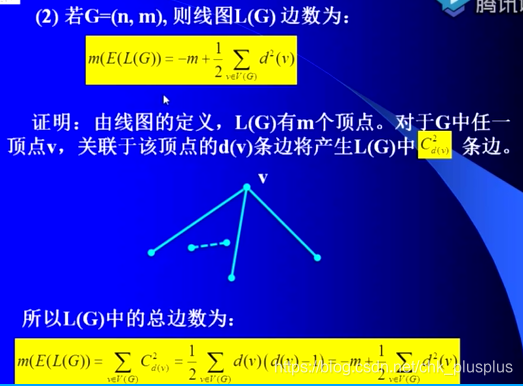
从线图的角度考虑欧拉图与哈密尔顿图关系（考试不作要求）

 

电子科技大学《图论及其应用》复习总结--第四章 欧拉图与哈密尔顿图
进击的搬砖猿
08-21 9015
第四章 欧拉图与哈密尔顿图 (一)、欧拉图及其性质 (1)、问题背景—欧拉与哥尼斯堡七桥问题 问题：对于图G，它在什么条件下满足从某点出发，经过每条边一次且仅一次，可以回到出发点？ 注：一笔画----中国古老的民间游戏（存在欧拉迹） 要求：对于一个图G, 笔不离纸, 一笔画成. 拓展：三笔画：在原图上添加三笔，可使其变为欧拉图。 定义1 对于连通图G，如果G中存在经过每条边的闭迹，则称G为欧拉图，简称G为E图。欧拉闭迹又称为欧拉环游，或欧拉回路。 定理1 下列陈述对于非平凡连通图G是等价的： ​
电子科技大学 图论期末复习 公式快速索引
qq_40892511的博客
08-24 4708
title: 图论期末考试复习 date: 2020-08-24 09:01:09 tags: 参考资料：《图论及其应用》 高等教育出版社 张先迪 / 李正良 仅用于复习参考，公式或多有误，请以教材为准。 文章目录title: 图论期末考试复习 date: 2020-08-24 09:01:09 tags:引言**第一章 图的基本概念**图与简单图图的定义及其相关概念图的同构作业题P29—P30 3, 4, 5, 6完全图偶图与补图定理1：若n阶图G是自补图，则有：![在这里插入图片描述.
哈密尔顿图
07-24
哈密尔顿图····················
图论复习（二）-——哈密顿图及其应用
weixin_45550092的博客
01-05 2万+
哈密顿图与半哈密顿图前言一、半/哈密顿图定义二、半/哈密顿图的必要条件三、判别二部图是否为哈密顿图四、判断哈密顿路的充分条件五、图的闭包、竞赛图六、哈密顿图的充要条件七、旅行商问题 前言 提示：本文主要介绍哈密顿图和半哈密顿图的定义以及判定条件，文中的图片来源于杨映雪老师的ppt。 一、半/哈密顿图定义 1.哈密顿路：给定无向图G中，通过图中每个结点一次而且仅一次的路径。 2.哈密顿回路：给定无向图G中，通过图中每个结点一次而且仅一次的回路。 3.哈密顿图：具有哈密顿回路的图。 4.半哈密顿图：有哈密顿路
求出所有哈密尔顿图
jxnczyp的专栏
06-10 1149
#include  #define   MAXSIZE  30         /*结点数小于30 */#define   ALWAYS    1         /*这是一个ＮＰ完全性问题*/#define   SUCCESS   1         /*所以结点不能过多，否则等很久*/#define   FAILURE   0#define   YES       1#define   N
图论理论总结
06-10
#### 四、欧拉图与哈密尔顿图 **4.1 欧拉图** - **定义**：一个连通图G是欧拉图当且仅当它的每个顶点的度都是偶数。 - **等价条件**：G的边集能划分为边不重的圈的并。 - **欧拉迹**：连通图G有Euler迹当且仅当G...
电子科技大学《图论及其应用》复习（史上最全汇总）
weixin_30478923的博客
05-18 7289
一、重要概念 1. 图、简单图、图的同构、度序列与图序列、补图与自补图、两个图的联图、两个图的积图、偶图 图：一个图是一个有序对<V, E>，记为G=(V, E)，其中： 1) V是一个有限的非空集合，称为顶点集合，其元素称为顶点或点。用|V|表示顶点数；2) E是由V中的点组成的无序对构成的集合，称为边集，其元素称为边，且同一点对在E中可以重复出现多次。用|E...
电子科技大学 图论期末复习 公式索引
qq_40892511的博客
09-04 1438
title: 图论期末考试复习 date: 2020-08-17 09:01:09 tags: 参考资料：《图论及其应用》 高等教育出版社 张先迪 / 李正良 仅用于方便复习公式查阅，公式或多有误，请以教材为准。 文章目录title: 图论期末考试复习 date: 2020-08-17 09:01:09 tags:引言**第一章 图的基本概念**图与简单图图的定义及其相关概念图的同构作业题P29—P30 3, 4, 5, 6完全图偶图与补图定理1：若n阶图G是自补图，则有：n%4=0or.
图论讲义 图匹配 染色应用，H图，E图
11-23
图论讲义，图路树，连通书，匹配，染色理论，E图，H图等
哈密尔顿图的判定算法_徐凤生.pdf
09-27
哈密尔顿图的判定算法_徐凤生,提出了哈密尔顿图判定的一个充要条件, 并给出了具体的实现算法.用C语言设计了相应的程序验证了此算法。
【哈密顿图】算法分析
GuChengAi的博客
12-23 3834
通过回溯法和暴力枚举来解决哈密顿图问题。
图论及其应用-哈密尔顿图(alpha)
weixin_30632899的博客
04-12 567
图论及其应用-哈密尔顿图(alpha) 小结：2010-04。。todo 没有粘贴公式。 1重要的概念是 闭包。 注意 ppt定义4 2重点汇总与 闭包定理 3其他的2个定理对比：（第一阶级：是不是两个反面） 一个是 存在 不相邻的点u , v, 围绕 du + dv >=n; G 是H图，那么G+uv也是H图（66：增边） 满足du + ...
【哈密尔顿图】目录
半壶老酒
11-13 1432
http://blog.csdn.net/pi9nc/article/details/9219971 sgu 122 poj3780 hdu3414 hdu4337 hdu4324
【离散数学·图论】关于哈密顿图的判别条件总结
热门推荐
weixin_61792975的博客
05-13 2万+
涉及到判断哈密顿图的“充分条件”；“不是”哈密顿图的“充分条件”；以及染色法，完全偶图等等
【图论及其运用 — 电子科技大学】（四）第四章 欧拉图与哈密尔顿图（Euler 图与 Hamilton 图）
最新发布
青年有志
05-24 1983
一、欧拉图与中国邮路问题 (一)、欧拉图及其性质 1、欧拉图的概念 (1)、问题背景—欧拉与哥尼斯堡七桥问题 注：一笔画----中国古老的民间游戏 要求：对于一个图G, 笔不离纸, 一笔画成. (2)、欧拉图概念 经过连通图 GGG 的每条边的迹被称为 Euler 迹（欧拉迹）（欧拉迹不要求回到原点，经过所有的点与边） 定义1 对于连通图GGG，如果GGG中存在经过每条边的 闭迹（即 Euler 闭迹），则称GGG为欧拉图，简称GGG为EEE图。欧拉闭迹又称为g游，或欧拉回路。（欧拉图是含有一条欧拉闭迹，
超级立方体小记
一刀不二
06-15 6401
在多指令流多数据流MIMD里面有用到基于超立方体互联的网络， 用《图论导引》里面简单的描述，就是处理器能通信，当且仅当他们的邻接（k元祖代表了处理器的地址） 一个 k 维立方体（或者超立方体Qk）是一种简单图，每个顶点{0,1}标记的k元祖来表示。 相邻的顶点之间的 k 元祖只有一个位置上数字不同，Qk 的生成立方体 Qj 和 Qj 本身同构。 这是Q3的表示：
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值