【图论及其运用 — 电子科技大学】（四）第四章 欧拉图与哈密尔顿图（Euler 图与 Hamilton 图）

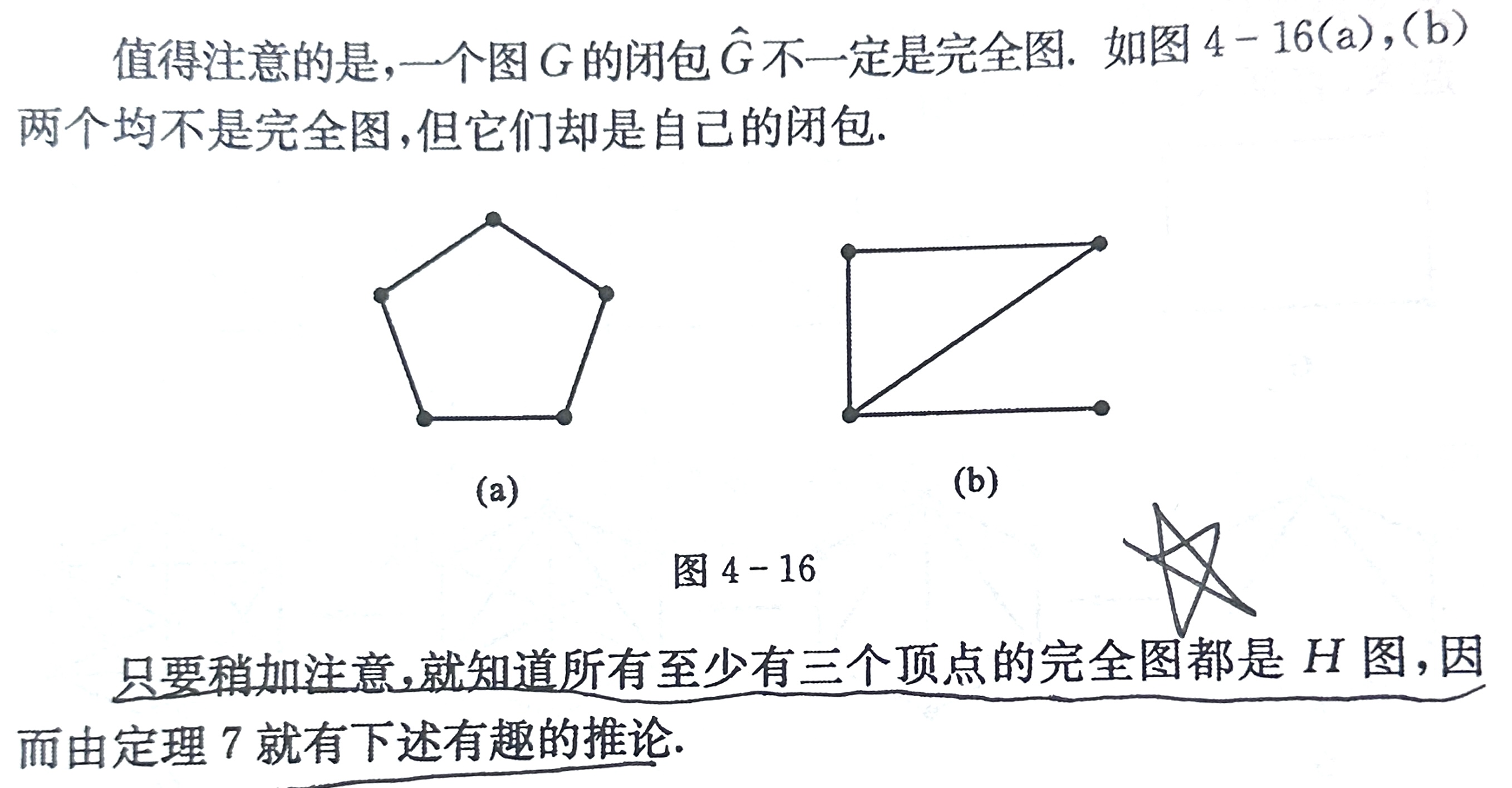
一、欧拉图与中国邮路问题

(一)、欧拉图及其性质

1、欧拉图的概念

(1)、问题背景—欧拉与哥尼斯堡七桥问题

注：一笔画----中国古老的民间游戏
要求：对于一个图G, 笔不离纸, 一笔画成.

(2)、欧拉图概念

经过连通图 $G$ 的每条边的迹被称为 Euler 迹（欧拉迹）（欧拉迹不要求回到原点，经过所有的点与边）

定义1 对于连通图$G$，如果$G$中存在经过每条边的 闭迹（即 Euler 闭迹），则称$G$为欧拉图，简称$G$为$E$图。欧拉闭迹又称为g游，或欧拉回路。（欧拉图是含有一条欧拉闭迹，需要回到原点的迹，注意与欧拉迹区分，欧拉迹只需要经过所有的点与边。但是不能重复经过）

2、欧拉图的性质

定理1 下列陈述对于非平凡连通图$G$是等价的：

(1) $G$ 是欧拉图；
(2) $G$ 的顶点度数为偶数；
(3) $G$ 的边集合能划分为圈。

推论1 连通图$G$是欧拉图当且仅当$G$的顶点度数为偶数。

推论2 连通非欧拉图$G$存在欧拉迹当且仅当$G$中只有两个顶点度数为奇数。

---

---

例2 证明： 若$G$和$H$是欧拉图，则 $G\times H$ 是欧拉图。

证明： 首先证明：对任意$u\in V(G),v\in V(H)$,有：$$d(u)+d(v)=d((u,v))$$
事实上，设$z$是$u$的任意一个邻点，一定有$(u,v)$的一个邻点$(z,v)$,反之亦然。同理，对于$v$的任意一个邻点$w$，一定有$(u,v)$的一个邻点$(u,w)$, 反之亦然。即: $(u,v)$在乘积图中邻点个数等于$u$在$G$中邻点个数与$v$在$H$中邻点个数之和。

所以，$G,H$ 是欧拉图，那么 $G\times H$ 顶点度数为偶数。
其次证明：$G\times H$ 是连通的。$$\forall (u_1,v_1),(u_2,v_2)\in V(G\times H)$$
由于$G,H$都是欧拉图，所以都连通。设最短的$u_1--u_2$路
最短的$v_1--v_2$路分别为：$u_1{x}_1{x}_2\cdots x_k{u}_2{v}_1{y}_1{y}_2\cdots y_m{v}_2$
那么，由乘积图的定义：在乘积图中有路：$(u_1,v_1)(x_1,v_1)\cdots (x_k,v_1)(u_2,v_1)(u_2,y_1)\cdots (u_2,y_m)(u_2,v_2)$
这样，我们证明了 $G\times H$ 是连通的且每个顶点度数为偶数。即它是欧拉图。

(二)、Fleury(弗勒里)算法

该算法解决了在欧拉图中求出一条具体欧拉环游的方法。方法是尽可能避割边行走。

案例： （除非万不得已，否走不走割边）

$A\to B$ 与 $A$ 相关联的边为 $e1,e2$，任选一条 $e1$

此时到达 $B$, 与 $B$ 相关联的边为 $e2,e3,e4$, $e2$ 为割边，不能走，在 $e3,e4$ 任选一条 $e3$

此时到达 $C$, 与 $C$ 相关联的边为 $e4$, $e4$ 为割边，但是没得选，因此选 $e4$

又走到 $B$，继续下去，即可。

---

再来看一个例子

---

---

---

---

(三)、中国邮路问题

1962年，中国数学家管梅谷提出并解决了“中国邮路问题”

1、问题

邮递员派信的街道是边赋权连通图。从邮局出发，每条街道至少行走一次，再回邮局。如何行走，使其行走的环游路程最短？

如果邮路图本身是欧拉图，那么由Fleury算法，可得到他的行走路线。

如果邮路图本身是非欧拉图，如何重复行走街道才能使行走总路程最短？

在一个赋权图中，环游 $v_0{e}_1{v}_1...e_n{v}_0$ 权定义为 ${\sum }_{i=1}^{n}w(e_i)$（边允许重复），则中国邮递员问题就是在具有非负权的赋权连通图中找出一条最小权的环游，这种环游称为最优环游。

若 $G$ 是 Euler 图，则任意的 Euler 环游都是最优环游

2、管梅谷的结论

解决最优环游的方法如下：
(1) 若图$G$是一个欧拉图，则找出$G$的欧拉回路即可。
(2) 对一般图，其解法为：添加重复边以使$G$成为欧拉图$G^{\ast }$，并使添加的重复边的边权之和为最小，再求$G^{\ast }$的欧拉回路。

如何确定添加的重复边的边权之和最小呢？管梅谷给出如下定理：

---

结合 定理1 $G$ 是欧拉图，当且仅当 $G$ 的每个点的度是偶数。

因此在求欧拉环游时，先找出待求图 $G$ 的所有奇度顶点

---

下图红色顶点为奇度顶点，共 10 个。(a) 到 (b) 为任意添加一些重复边，使得所有奇度点变为偶数。检查 (b) 中所有圈是否满足管梅谷结论

---

如下原图的奇点为 $v_2,v_3,v_7,v_6,v_5,v_4$

---

二、哈密尔顿图

强调： 关于哈密尔顿图问题，我们要重点掌握 1、性质定理的应用； 2、度序列判定法的应用； 3、闭包定理的应用

(一)、哈密尔顿图的概念

2、哈密尔顿图与哈密尔顿路

定义1 如果经过图$G$的每个顶点恰好一次后能够回到出发点，称这样的圈为哈密尔顿圈，存在 Hamilton 圈的图称为 Hamilton 图，简称$H$图。

Hamilton 路经过每个顶点一次，但是不需要回到起点

---

---

---

(二)、性质与判定

1、性质

☆☆☆☆ 定理1 (必要条件) 若$G$为$H$图，则对$V(G)$的任一非空顶点子集$S$，有：
$$\omega (G-S)\le \left|S\right|$$

用此定理判断非哈密尔顿图

---

注意： 满足定理1不等式的图不一定是$H$图。

---

2、判定

定理2 (充分条件) 对于$n\geqq 3$的单图$G$，如果$G$中有：$\delta (G)\ge \frac{n}{2}$ 那么$G$是$H$图。

充分条件而不是必要条件，说明，$\delta (G)\ge \frac{n}{2}$ 一定是 $H$ 图，而 $H$ 图，不一定满足 $\delta (G)\ge \frac{n}{2}$

定理3 (充分条件) 对于$n\geqq 3$的单图$G$，如果$G$中的任意两个不相邻顶点$u$与$v$，有：$d(u)+d(v)\ge n$ 那么，$G$是$H$图。

注： (1) 该定理证明和定理2可以完全一致！

(2) 该定理的条件是紧的。 例如：设$G$是由$K_{k+1}$的一个顶点和另一个$K_{k+1}$的一个顶点重合得到的图，那么对于$G$ 的任意两个不相邻顶点$u$与$v$，有：$d(u)+d(v)=2k=n-1$ 但$G$是非$H$图。

引理1（充要条件） 对于单图$G$，如果$G$中有两个不相邻顶点$u$与$v$，满足：$d\left(u\right)+d\left(v\right)\ge n$ 那么$G$是$H$图当且仅当$G+uv$是$H$图。

证明：略

定义3 在$n$阶单图中，若对$d(u)+d(v)\geqq n$ 的任意一对顶点$u$与$v$，均有$uadjv$ , 则称$G$是 闭图。

第一个图的 $n$ 为 4，每个点的度为 2，对角满足 $d(u)+d(v)\geqq n$，但不是邻接，而第二个图没有满足 $d(u)+d(v)\geqq n$ 条件的点对。

---

非闭图可以通过连边的形式变为闭图，即引出如下定理

引理2 若$G_1$和$G_2$是同一个点集$V$的两个闭图，则$G=G_1\cap G_2$是闭图。（了解即可，不要求掌握）

证明： 任取$u,v\in V(G1\cap G2)$，如果有：$$d_G(u)+d_G(v)\ge n$$
易知：$$d_{G_1}\left(u\right)+d_{G_1}\left(v\right)\ge n,d_{G_2}\left(u\right)+d_{G_2}\left(v\right)\ge n$$
因$G_1$与$G_2$都是闭图，所以$u$与$v$在$G_1$与$G_2$中都邻接，所以，在$G$中也邻接。故$G$是闭图。

---

定义4 称 $\hat{G}$ 是图 $G$ 的闭包，如果它是包含$G$的极小闭图。

将图片中 $\bar{G}$ 看作是 $\hat{G}$

引理3 图$G$的闭包是唯一的。(证明略)

定理4(帮迪——闭包定理) 图$G$是$H$图当且仅当它的闭包 $\hat{G}$ 是$H$图。

由于完全图一定是$H$图，所以由闭包定理有：

推论1： 设$G$是$n\geqq 3$的单图，若$G$的闭包是完全图，则$G$是$H$图。

由闭包定理也可以推出Dirac和Ore定理：

推论2： 设$G$是$n\geqq 3$的单图。若$\delta (G)\geqq n/2$, 则$G$是$H$图 (Dirac定理); 上面有详细证明，下面用闭包定理证明

证明： 因为满足条件的图的闭包一定是完全图。由闭包定理得到证明。

推论3： 设$G$是$n\geqq 3$的单图。若对于$G$中任意不相邻顶点$u$与$v$，都有$d(u)+d(v)\geqq n$, 则$G$是$H$图.(Ore定理)上面有详细证明，下面用闭包定理证明

证明： 因为满足条件的图的闭包一定是完全图。由闭包定理得到证明。

在闭包定理的基础上，Chvátal和帮迪进一步得到图的H性的度序列判定法。（只理解认识并运用即可，不用证明）

☆☆☆☆☆定理5(Chvátal——度序列判定法) 设简单图$G$的度序列是($d_1,d_2,\dots ,d_n$), 这里，$d_1\leqq d_2\leqq \dots \leqq d_n$, 并且$n\geqq 3$. 若对任意的$m<n/2$, 或有 $d_m>m$, 或有$d_{n-m}\geqq n-m$, 则$G$是$H$图。

定理5的逆否命题： 设简单图$G$的度序列是($d_1,d_2,\dots ,d_n$), 这里，$d_1\leqq d_2\leqq \dots \leqq d_n$,并且 $n\geqq 3$. 若存在$m<n/2$, 有 $d_m\le m$ ,且有 $d_{n-m}<n-m$, 则$G$是非$H$图。

---

采用 度序列判定法 来做（考试频率极高）如果违反这个定理，也许是 H 图也许不是

第一步：从小到大写度序列（下图 9 个顶点）
第二步：枚举 m，$m<n/2$ （9/2 = 4.5），注意是任意 m，所以需要满足所有情况
第三步：对每个 m 进行检验，满足或有 $d_m>m$, 或有$d_{n-m}\geqq n-m$

说明：m = 1, 2, 3, 4，依次检验 $d_1=3>1$ 满足， $d_2=3>2$ 满足，$d_3=3=3$ 不满足 > 3， $d_{9-3}=d_6=6\geqq 9-3$，因此 m = 3 满足，$d_4=5>4$，满足，因此$G$是$H$图

---

作业

P97—99 习题4 ： 10, 12

三、度极大非哈密尔顿图与TSP问题

(一)、度极大非哈密尔顿图

回顾度弱于度优关系

结论： $G_1$ 度弱于 $G_2$, 则 $m(G_1)\le m(G_2)$. （握手定理可以说明）

回顾联运算

1、定义

定义1 图$G$称为度极大非$H$图，如果它的度不弱于其它非$H$图。

注： 极大 $H$ 图，与度极大 $H$ 图是不一样的，极大 $H$ 图是表示在不邻接顶点对，连接一条边后，就会变为 $H$ 图

2、$C_{m,n}$ 图（重点要求，n 固定，根据 m 的不同取值，得到一些列的 $C_{m,n}$ 图，为图族）

定义2 对于 $1\leqq m<n/2,C_{m,n}$ 图定义为：$$C_{m,n}=K_m\vee ({\bar{K}}_m+K_{n-2m})$$

对于 1$\le m<n/2,Cm,n$ 图：对$\forall S\subseteq X$ ,有$\left|N\left(S\right)\right|\ge \left|S\right|$

---

3、$C_{m,n}$ 的性质

引理1 对于$1\leqq m<n/2$的图$C_{m,n}$是非$H$图。

$d(v)=m+(m-1)+(n-2m)$ 是对于 $C_{m,n}$ 中 $K_m$ 的一个顶点自身其他顶点连接 m - 1， 与 $\overline{K_m}$ 连接 m， $K_{n-2m}$ 为 n - 2m

4、度极大非$H$图的特征

定理1 (Chvátal,1972) 若$G$是$n\geqq 3$的非$H$单图，则$G$度弱于某个$C_{m,n}$图。（Chvátal 还证明了度序列判定定理）（这里的度弱于某个 $C_{m,n}$图，是因为下面证明中是存在 $m<n/2$）

(1) 定理1 刻画了非 $H$ 单图的特征：从度序列角度看，$C_{m,n}$ 图族中某个图是某个 $n$ 阶非 $H$ 单图的极图。

(2) 定理的条件是充分条件而非必要条件。

(3) 如果$n$阶单图$G$度优于所有的$C_{m,n}$图族，则$G$是$H$图。

---

推论（充分条件） 设$G$是$n$阶单图。若 $n\geqq 3$ 且$\left|E(G\right)|>\left(\genfrac{}{}{0ex}{}{n-1}{2}\right)+1$ , 则$G$是$H$图；并且，具有$n$个顶点和$(\begin{array}{c}n-1\\ 2\end{array})+1$ 条边的非$H$图只有$C_{1,n}$以及当 $n=5$ 时，还有$C_{2,5}$.

---

---

注： 推论的条件是充分而非必要的。

---

通过添加一个点来说明，很美妙的思维！

---

两个子集不相等的偶图，一定不存在 $H$ 圈

---

(二)、TSP问题

TSP问题即旅行售货员问题，是应用图论中典型问题之一。问题提法为：一售货员要到若干城市去售货，每座城市只经历一次，问如何安排行走路线，使其行走的总路程最短

在赋权图中求最小$H$圈是 NP 难问题。理论上也已经证明：不存在多项式时间近似算法，使相对误差小于或等于某个固定的常数 $\epsilon$,即便是 $\epsilon =1000$ 也是如此。

1、边交换技术（近似解）

---

通过初始化时选择不同的 $H$ 圈来尝试寻找更优的解，那是否有个下界呢？

---

2、最优$H$圈的下界（期末考过 ☆☆☆☆☆）

可以通过如下方法求出最优$H$圈的一个下界：

• (1) 在$G$中删掉一点$v$(任意的)得图$G_1$;
• (2) 在图$G_1$中求出一棵最小生成树$T$;
• (3) 在$v$的关联边中选出两条权值最小者$e_1$与$e_2$.

若$H$是$G$的最优圈，则：
$$W\left(H\right)\ge W\left(T\right)+W\left(e_1\right)+W\left(e_2\right)$$

---

满足条件后：$W\left(T\right)+W\left(e_1\right)+W\left(e_2\right)$ 即为最优 $H$ 圈的下界，下界不唯一 ，删除顶点不一样，下界或许不一样，因此可以通过遍历删除每个顶点，下界越大越好

---

---

P97—99 习题4 ： 13, 14，17

四、超哈密尔顿图与超可迹图问题

(一)、超$H$图与超$H$迹

定义1 若图$G$是非$H$图，但对于$G$中任意点$v$, 都有$G-v$是$H$图，则称$G$是超$H$图。

定理1 彼得森（Peterson）图是超$H$图。

---

---

---

定义2 若$G$中没有$H$路，但是对$G$中任意点$v$，$G-v$存在$H$路，则称$G$是超可迹的。

数学家加莱曾经猜想：不存在超可迹的图。但该猜想被Horton和Thomassen以构图的方式否定了。

定理2 Thomassen图是超可迹图。

---

---

关于H图的一些猜想

1、加莱猜想：不存在超可迹的图。

2、泰特猜想：任何3连通3正则可平面图是H图。

3、纳什—威廉斯猜想：每个4连通4正则图是H图。

4、托特猜想：每个3连通3正则偶图是H图。

5、普鲁默猜想：每个2连通图的平方是H图。（该猜想是正确的，已经得到证明。）

定义： 图$G$的平方$G^2$是这样的图:

值得一提的是：在H问题研究中，H图中H圈的计数问题也是一个研究方向。

定理：每个3正则H图至少有3个生成圈。

(二)、$E$ 图和 $H$ 图的关系（重点）

从表面上看，$E$ 图与$H$图间没有联系。因为我们可以不费力地找到： (1) $E$图但非$H$图；(2) $E$图且$H$图；(3) $H$图但非$E$图; (4) 非$E$图且非$H$图.

1、线图概念

定义3 设$G$是图，$G$的线图$L(G)$定义为：（线图$L(G)$的顶点集合正好等于原图$G$的边集合，且两条边属于线图当且仅当这两条边在原图中邻接）

$$V(L(G))=E(G)$$

$$(e_1,e_2)\in E(L(G))\iff \text{在}G\text{中有:边}{e}_1\text{与}{e}_2\text{邻接}$$

实际上就是将边的邻接转换为点的邻接，是因为研究点好研究一些。

特别地，定义$G$的$n$次迭线图$L^n(G)$ 为：$L^n(G)=L(L^{n-1}(G))$

$G_1$ 到 $G_2$ 实际上就是将原图的边变为点，可以看到，线图的点数就是原图的边数，

2、线图的性质

(1) 线图$L(G)$顶点数等于$G$的边数；若$e=uv$是$G$的边，则$e$作为$L(G)$的顶点度数为：$d(e)=d(u)+d(v)-2$ .

(2) 若$G=(n,m)$, 则线图 $L(G)$ 边数为：
$$m(E(L(G))=-m+\frac{1}{2}\sum _{v\in V(G)}{d}^2(v)$$

证明： 由线图的定义，$L(G)$ 有 $m$ 个顶点。对于 $G$ 中任一顶点 $v$，关联于该顶点的 $d(v)$ 条边将产生 $L(G)$ 中 $C_{d(v)}^2$ 条边。所以 $L(G)$ 中的总边数为：（$C_{d(v)}^2$ 是因为原图 $G$ 中，任意与 $v$ 相邻的两个点与$v$组成两条边，且这两条边在 $L(G)$ 中用点表示，并相邻，因此两两组合，产生 $C_{d(v)}^2$ 条边）

$$m(E(L(G))=\sum _{v\in V(G)}{C}_{d(v)}^2=\frac{1}{2}\sum _{v\in V(G)}d(v)(d(v)-1)=-m+\frac{1}{2}\sum _{v\in V(G)}{d}^2(v)$$

(3) 一个图同构于它的线图，当且仅当它是圈。
(4) 若图G和$G_1$有同构的线图，则除了一个是$K_3$而另一个是$K_{1,3}$外，$G$和$G_1$同构。(证明比较复杂)

3、从线图的角度考察E图与H图的关系（了解即可）

定义4 称$S_n$是图$G$的$n$次细分图，是指将$G$的每条边中都插入$n$个$2$度顶点。

定理3
(1)若G是E图，则L(G) 既是E图又是H图。
(2)若G是H图，则L(G)是H图。

定理4 一个图 $G$ 是 $E$ 图的充要条件是 $L_3(G)$ 为 $H$ 图

定理5 （Chartarand）若$G$ 是$n$个点的非平凡连通图，且不是一条路，则对所有$m\ge n-3，L_m(G)$ 是 $H$ 图。