一 特殊平面图
1 极大平面图及其性质

极大平面图的两种情况,一种是K1到K4四种特殊情况,即1阶到4阶的完全图是极大可平面图
另一种就是一般的情况,任意非邻接顶点间添加一条边后,得到的图均是非可平面图。













二、平面图的对偶图




一 特殊平面图
1 极大平面图及其性质

极大平面图的两种情况,一种是K1到K4四种特殊情况,即1阶到4阶的完全图是极大可平面图
另一种就是一般的情况,任意非邻接顶点间添加一条边后,得到的图均是非可平面图。













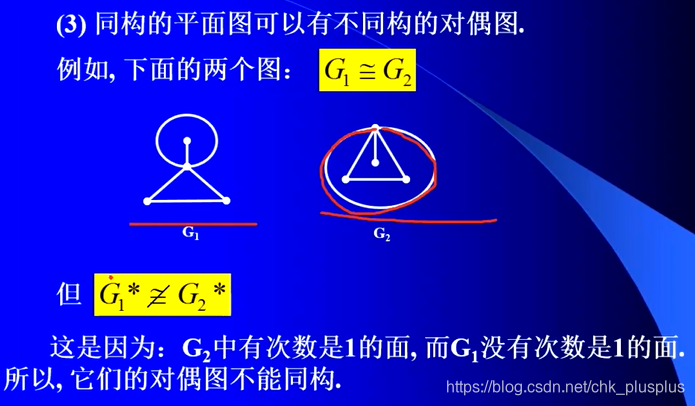
二、平面图的对偶图





 5862
5862
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


