1.PCA理论介绍
Principal Component Analysis(PCA)是最常用的线性降维方法,它的目标是通过某种线性投影,将高维的数据映射到低维的
空间中表示,并期望在所投影的维度上数据的方差最大,以此使用较少的数据维度,同时保留住较多的原数据点的特性。
通俗的理解,如果把所有的点都映射到一起,那么几乎所有的信息(如点和点之间的距离关系)都丢失了,而如果映射后方差
尽可能的大,那么数据点则会分散开来,以此来保留更多的信息。可以证明,PCA是丢失原始数据信息最少的一种线性降维方式。
(实际上就是最接近原始数据,但是PCA并不试图去探索数据内在结构)
在具体介绍PCA之前,先来了解一下协方差矩阵的概念。
协方差总是在两维数据之间进行度量,如果我们具有超过两维的数据,将会有多于两个的协方差。例如对于三维数据(x, y, z维),需要计算cov(x,y),cov(y,z)和cov(z,x)。获得所有维数之间协方差的方法是计算协方差矩阵。维数据协方差矩阵的定义为
这个公式告诉我们,如果我们有一个n维数据,那么协方差矩阵就是一个n行n列的方矩阵,矩阵的每一个元素是两个不同维数据之间的协方差。
对于一个3维数据(x,y,z),协方差矩阵有3行3列,它的元素值为:
需要注意的是:沿着主对角线,可以看到元素值是同一维数据之间的协方差,这正好是该维数据的方差。对于其它元素,因为cov(a,b)=cov(b,a),所以协方差矩阵是关于主对角线对称的。
在介绍了协方差矩阵的概念后,我们来看一下PCA的计算过程:
1)获取数据
2)减去均值
3)计算协方差矩阵
4)计算协方差矩阵的特征矢量和特征值
5)选择特征值最大的K个特征值对应的特征向量作为主成分
6)用主成分矩阵乘以原始数据得到降维后的数据
举例说明:
假设我们得到的2维数据如下:
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。可以这样认为,有10篇文档,x是10篇文档中“learn”出
现的TF-IDF,y是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车,x是千米/小时的速度,y是英里/小时的速度等。
第一步分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,那么一个样例
减去均值后即为(0.69,0.49),得到
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是
这里只有x和y,求解得
<








 PCA(主成分分析)是一种线性降维方法,旨在通过最大化投影后的方差来保留数据的主要特性。它包括计算协方差矩阵、特征值和特征向量,选择最大特征值对应的特征向量作为主成分。PCA适用于数据预处理,减少特征维度,但可能不适用于分类任务,因为它不考虑类别区分性。
PCA(主成分分析)是一种线性降维方法,旨在通过最大化投影后的方差来保留数据的主要特性。它包括计算协方差矩阵、特征值和特征向量,选择最大特征值对应的特征向量作为主成分。PCA适用于数据预处理,减少特征维度,但可能不适用于分类任务,因为它不考虑类别区分性。
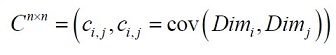
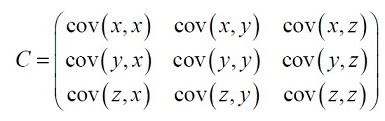
![clip_image001[4] clip_image001[4]](https://i-blog.csdnimg.cn/blog_migrate/989d7d47ae20a177a278b170f5770741.png)
![clip_image002[4] clip_image002[4]](https://i-blog.csdnimg.cn/blog_migrate/827b8f5f38dd8c6586334a2da3b061c5.png)
![clip_image003[4] clip_image003[4]](https://i-blog.csdnimg.cn/blog_migrate/2ca70e462fad739a74a8a4b1e824ce90.png)
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 708
708

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








