51nod 1052 最大M子段和 （区间dp）

看到大佬题解，感觉很全面

动态规划，借助矩阵可以直观的看到计算过程。

定义二维数组dp， dp[ i ][ j ]，表示前 j 项所构成 i 子段的最大和，且必须包含着第j项，即以第j项结尾

然后是一个递推过程。

求dp[ i ][ j ]，有两种情况

1、dp[ i ][ j ] = dp[ i ] [ j-1 ] + a[ j ] ，即把第j项融合到第 j-1 项的子段中，子段数没变

2、dp[ i ][ j ] = dp[ i-1 ] [ t ] + a[ j ]，（i-1<= t < j ）

把第 j 项作为单独的一个子段，然后找一下i-1个子段时，最大的和，然后加上a[ j ] 

然后比较上面两种情况，取大的。

下面看图，红色数字为输入的序列：

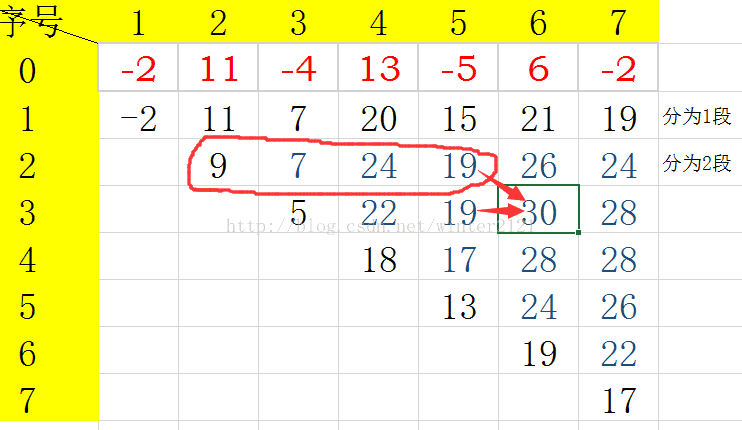可以看出dp[3][6]只和dp[3][5]和上一行中红色圈中的有关，所以把上一行用pre这个一维数组来表示，他们的最大值用一个数表示，每次记得跟更新就行了。

我要说一下我自己对这个题的理解，首先看到题，我想到的是区间dp，区间dp需要三重循环就是n^3是不能解决问题的，我直接否定了它，正确的dp思路（我以为的）应该是先去想怎么能在分成k组的时候用到k-1组的数据。所以dp数组应该是二维的其中一维表示分成几组，dp[i][j]表示分成i组，j应该表示什么应该是以j为结尾。里面必须有a[j]。那我们就会去想如果一个没有a【j】的数最大怎么办，我们可以用ans一直更新比ans大的数。dp[i][j]应该是谁递推而来的呢，肯定是前一行位置j之前的最大值，和这一行前面的dp[i][j-1]。我们现在想前面的j之前的最大值，每一次都要更新j，这不还是n^3，事实上o(1)就可以得到 前一行位置j之前的最大值，这样就出来了o（n^2）的算法。

为什么算原创的，因为，我只是用了那个dalao部分说明和图片

#include<bits\stdc++.h>
typedef long long ll;
using namespace std;
int n,m;
        ll a[5050];
        ll dp[5002]={0};
        ll pre[5002]={0};//记录上一行
int main()
{
       scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]);
        long long ans=-(1 << 30);
        for(int i=1;i<=m;i++)
        {
            dp[i]=pre[i-1]+a[i];//先假设为左上角那个元素为最优值
            ll maxpre=pre[i-1]; //maxpre记录上一行的最大值
            for(int j=i;j<=n;j++)
            {
                dp[j]=max(dp[j-1],maxpre)+a[j];
                ans=max(ans,dp[j]);
                maxpre=max(maxpre,pre[j]);
                pre[j]=dp[j];
            }
        }
       cout<<ans<<endl;
    return 0;
}