【上一篇 2 从Multi-arm Bandits问题分析 - RL进阶】
【下一篇 4 动态编程(Dynamic Programming, DP)】
本次总结中的 1-4 小节主要介绍了增强学习中的一些重要的概念,如:Goals、Rewards、Returns、Episode 等,第 5 小节介绍了 Markov Property,第 6 小节介绍了 Markov Decision Processes,第 7、8 小节介绍了 RL 中的 Value Function。可以说这次总结也是为之后介绍 RL 相关算法做了铺垫。
1 增强学习中的一般模型
在强化学习(Reinforcement Learning, RL)初步介绍中曾经介绍了 RL 问题的一般模型,下面再简单回顾一下:
在 RL 中,agents 是具有明确的目标的,所有的 agents 都能感知自己的环境,并根据目标来指导自己的行为,因此 RL 的另一个特点是它将 agents 和与其交互的不确定的环境视为是一个完整的问题。在 RL 问题中,有四个非常重要的概念:
(1)规则(policy)
Policy 定义了 agents 在特定的时间特定的环境下的行为方式,可以视为是从环境状态到行为的映射,常用 π \pi π 来表示。policy 可以分为两类:
- 确定性的 policy(Deterministic policy): a = π ( s ) a=\pi(s) a=π(s)
- 随机性的 policy(Stochastic policy): π ( a ∣ s ) = P [ A t = a ∣ S t = t ] \pi(a|s)=P[A_t=a|S_t=t] π(a∣s)=P[At=a∣St=t]
其中, t t t 是时间点, t = 0 , 1 , 2 , 3 , … … t=0,1,2,3,…… t=0,1,2,3,……
S t ∈ S S_t\in{\mathcal{S}} St∈S, S {\mathcal{S}} S是环境状态的集合, S t S_t St代表时刻 t t t 的状态, s s s 代表其中某个特定的状态;
A t ∈ A ( S t ) A_t\in{\mathcal{A}}(S_t) At∈A(St), A ( S t ) {\mathcal{A}}(S_t) A(St) 是在状态 S t S_t St 下的 actions 的集合, A t A_t At 代表时刻 t t t 的行为, a a a 代表其中某个特定的行为。
(2)奖励信号(a reward signal)
Reward 就是一个标量值,是每个 time step 中环境根据 agent 的行为返回给 agent 的信号,reward 定义了在该情景下执行该行为的好坏,agent 可以根据 reward 来调整自己的 policy。常用 R R R 来表示。
(3)值函数(value function)
Reward 定义的是立即的收益,而 value function 定义的是长期的收益,它可以看作是累计的 reward,常用 v v v 来表示。
(4)环境模型(a model of the environment)
整个Agent和Environment交互的过程可以用下图来表示:
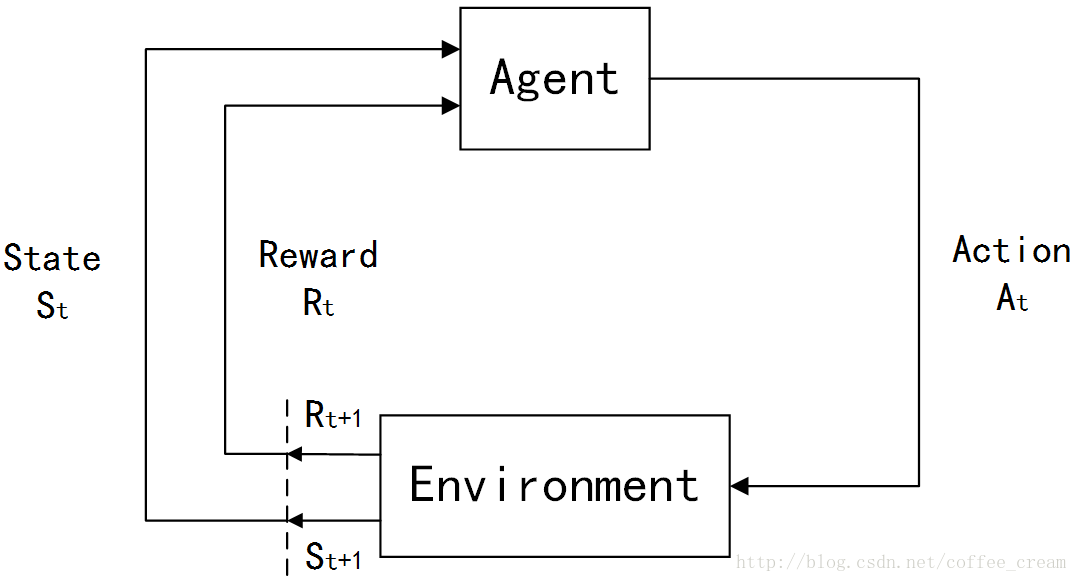
其中, t t t 是时间点, t = 0 , 1 , 2 , 3 , … … t=0,1,2,3,…… t=0,1,2,3,……
S t ∈ S S_t\in{\mathcal{S}} St∈S, S {\mathcal{S}} S 是环境状态的集合;
A t ∈ A ( S t ) A_t\in{\mathcal{A}}(S_t) At∈A(St), A ( S t ) {\mathcal{A}}(S_t) A(St) 是在状态 S t S_t St 下的 actions 的集合;
R t ∈ R ∈ R R_t\in{\mathcal{R}}\in{\Bbb R} Rt∈R∈R 是数值型的 reward。
在每个时间步骤中,agent 都会实现一个从 states 到每个可能的 actions 的 probabilities 的映射,这个映射函数就称作是这个 agent 的 p o l i c y policy policy,常用符号 π t \pi_t πt 来表示, π t ( a ∣ s ) \pi_t(a|s) πt(a∣s) 指的就是在状态 S t = s S_t=s St=s 下选择执行 A t = a A_t=a At=a 的概率。
其实概括的来说,不同的 RL 方法的主要不同就是利用 experience 来改变自己的 π t \pi_t πt 的方法,毕竟RL 就是从 experience 中进行学习的一系列方法。
2 Goals 和 Rewards
在 RL 中,goals 和 rewards 是两个重要的概念,在每个时间步骤中,环境返回给 Agent 的 reward 就是一个简单的数值,而 Agent 的 goal 就是最大化它接受到的所有的 reward signal 的和,也就是说,它的目的不是最大化当前步骤的立即获得的 reward ,而是一个长远的目标,并且需要注意的是,这个 reward 是由 environment 定义的而非 Agent。
3 Returns
刚刚提到,Agent 的 goal 就是最大化它接受到的所有的 reward signal 的和,那么就需要将这个目标值用函数的形式来表达出来,这里令时间 t t t 获得的 reward 为 R t + 1 , R t + 2 , R t + 3 , … R_{t+1}, R_{t+2}, R_{t+3}, \ldots Rt+1,Rt+2,Rt+3,… ,令 G t G_t Gt 代表期望的 return,那么最简单的 return 的形式为:
G t ≐ R t + 1 + R t + 2 + R t + 3 + … + R T (1) G_t \doteq R_{t+1}+R_{t+2}+R_{t+3}+\ldots +R_T \tag{1} Gt≐Rt+1+Rt+2+Rt+3+…+RT(1)
其中, T T T 代表最后一个的时间步骤。
这时就需要再引入一个新的概念 episodes,翻译成中文的话就是“片段、插曲”的意思,这里指的是一个可以自然结束的 agent-environment 交互的过程,每个 episode 都会在一个特殊的状态下结束,这个状态就称作是 terminal state,因此每个 episode 的相同点是它们都以 terminal state 来结束,不同就是每个 episode 获得的 reward 不同,采用 episodes 形式的 tasks 就称为是 episodic tasks,在episodic tasks 中,常常将所有非终止的状态的集合记为是 S {\mathcal{S}} S,而把包含终止状态的所有状态的集合记为是 S + {\mathcal{S}}^+ S+。
与 episode task 相对应的另外一种是 continuing tasks,它们指的是那些不会自然结束,会一直持续进行的 task,这时 return 公式(1)中的 T = ∞ T=\infty T=∞。
还有一个比较重要的概念是 Discounting,它是对未来不同时刻的 reward 赋予不同的权重,距离现在较近的 reward 的权重较高,而时间越远的权重越低,这时选择行为 A t A_t At 的准则就是最大化期望的 Discounted Return:
G t ≐ R t + 1 + γ R t + 2 + γ 2 R t + 3 + … = ∑ k = 0 ∞ γ k R t + k + 1 G_t \doteq R_{t+1}+{\gamma}R_{t+2}+{\gamma}^2R_{t+3}+\ldots =\sum_{k=0}^{\infty}{\gamma_k R_{t+k+1}} Gt≐Rt+1+γRt+2+γ2Rt+3+








 本文详细介绍了强化学习中的一般模型,包括Goals、Rewards、Returns和Episodic与Continuing Tasks。重点讲解了马尔可夫性质与马尔可夫决策过程(MDPs),并探讨了Value Functions和Optimal Value Functions,为后续RL算法的学习奠定了基础。
本文详细介绍了强化学习中的一般模型,包括Goals、Rewards、Returns和Episodic与Continuing Tasks。重点讲解了马尔可夫性质与马尔可夫决策过程(MDPs),并探讨了Value Functions和Optimal Value Functions,为后续RL算法的学习奠定了基础。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1145
1145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








