MIMO信道容量（即系统能够传输的最大信息速率，不会引起误差）的推导

引言

以下是信道矩阵 $\mathbf{H}$ 的奇异值的一些重要作用：

1. 信道容量分析：想象你的通信系统是一条多车道的高速公路，每条车道就像是一个可以传输信息的通道。信道容量就是这些车道可以安全运输信息的最大速率。在MIMO系统中，我们可以通过检查信道矩阵的奇异值来估算这个最大速率。奇异值的平方告诉我们每条车道可以承载多少信息。

2. 信号分解和空间复用：通过一种叫做奇异值分解（SVD）的技巧，我们可以把复杂的多车道高速公路变成多个单车道的直线路段，每个直线路段对应一个奇异值。这样，我们就可以在每个直线路段上独立地发送信息，就好像每个路段都是自己的私人道路一样。

3. 预编码设计：在发送信息前，我们可以通过一种称为预编码的方法调整信号，以适应当前的通信条件，就像根据天气和交通状况调整你的行车路线一样。利用SVD，我们可以根据信道矩阵的特定向量来调整信号，以此来确保信息传输尽可能清晰。

4. 抗干扰与抗衰落：在MIMO系统中，我们可以通过调整我们的信号发送策略来对抗干扰和信号衰减。如果我们发现某些“车道”（子信道）条件很差（即对应的奇异值很小），我们就可以选择不在这些车道上发送信息，从而提高整体的传输效率和质量。

5. 系统性能评估：信道矩阵的奇异值可以帮助我们了解通信信道的质量。如果最小的奇异值都相对较大，这意味着即使是条件最差的车道也表现得不错，说明整个MIMO通信系统的性能很好。

简而言之，信道矩阵的奇异值在设计和评估MIMO通信系统时扮演着重要的角色，它们帮助我们理解每个通道的传输能力，设计最佳的传输策略，并评估整个系统的性能。

所以，本文我们通过介绍SVD及相关操作，引入各种条件下MIMO系统信道容量的推导。

简化解释SVD

考虑一个复数矩阵 $\mathbf{H}$，它具有 $N_{\mathrm{Rx}}$ 行和 $N_{\mathrm{Tx}}$ 列。这个矩阵可以通过一种特殊的方法（称为奇异值分解或SVD）被分解成三个部分：

$$\begin{array}{c}\mathbf{H}=\mathbf{U}\Sigma {\mathbf{V}}^{\mathrm{H}}\end{array}$$

1. $\mathbf{U}$ 矩阵 - 它是一个正方形矩阵，行和列的数量与 $\mathbf{H}$ 矩阵的行数相同。$\mathbf{U}$ 是一个酉矩阵，意味着它与其自身的共轭转置相乘等于单位矩阵（一个主对角线上全是1，其他地方全是0的矩阵）。

2. $\Sigma$ 矩阵 - 这是一个对角矩阵，意味着除了主对角线外，其他元素都是0。对角线上的元素是非负实数，称为矩阵 $\mathbf{H}$ 的奇异值。

3. ${\mathbf{V}}^{\mathrm{H}}$ 矩阵 - 类似于 $\mathbf{U}$，它是一个酉矩阵，行和列的数量与 $\mathbf{H}$ 矩阵的列数相同。这里的 $\mathrm{H}$ 表示共轭转置。

酉矩阵和奇异值

• 酉矩阵：如果一个矩阵与其自身的共轭转置相乘等于单位矩阵，那么这个矩阵就是酉的。
• 奇异值：$\mathbf{H}$ 矩阵的奇异值是一些特定的值，可以从 $\Sigma$ 矩阵的对角线上找到。这些值给我们提供了关于矩阵的某些特性的信息，比如它的“秩”。

矩阵的秩

• 矩阵 $\mathbf{H}$ 的“秩”等于其非零奇异值的数量。这个数字最大可以是 $N_{\mathrm{Rx}}$ 和 $N_{\mathrm{Tx}}$ 中的较小值。

特征值和Frobenius范数

• 特征值：矩阵 $\mathbf{H}$ 的奇异值的平方实际上是两个特殊形式的矩阵（$\mathbf{H}{\mathbf{H}}^{\mathrm{H}}$ 或 ${\mathbf{H}}^{\mathrm{H}}\mathbf{H}$）的特征值。
• Frobenius范数：是一种衡量矩阵大小（或“能量”）的方法。对于 $\mathbf{H}$，它等于所有元素的平方和。通过SVD，我们可以将Frobenius范数表示为所有非零奇异值的平方和。

---

1. 有用的矩阵理论

矩阵 $\mathbf{H}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{Tx}}}$ 的奇异值分解 (Singular Value Decomposition, SVD) 可以表示为
$$\begin{array}{c}\mathbf{H}=\mathbf{U}\Sigma {\mathbf{V}}^{\mathrm{H}}\end{array}$$

其中, $\mathbf{U}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{Rx}}}$ 和 $\mathbf{V}\in {\mathbb{C}}^{N_{\mathrm{Tx}}\times N_{\mathrm{Tx}}}$ 都为酉矩阵 ； $\mathbf{\Sigma }\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{Tx}}}$ 为对角矩阵, 其对角线上的元素为非负实数, 非对角线上的元素为零。 $\mathbf{\Sigma }$ 的对角线元素是矩阵 $\mathbf{H}$ 的奇异值, 记为 ${\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_{N_{\min }}$,其中 $N_{\text{min }}\triangleq \min \left(N_{\mathrm{Tx}},N_{\mathrm{Rx}}\right)$ 。

酉矩阵: 酉矩阵 $\mathbf{U}$ 满足 ${\mathbf{U}}^{\mathrm{H}}\mathbf{U}={\mathbf{I}}_{N_{\mathrm{Rx}}}$, 其中 ${\mathbf{I}}_{N_{\mathrm{Rx}}}$ 是 $N_{\mathrm{Rx}}\times N_{\mathrm{Rx}}$ 的单位矩阵。

在实际中, 假设 ${\sigma }_1⩾{\sigma }_2⩾\cdots ⩾{\sigma }_{N_{\text{min }}}$, 即 $\mathbf{\Sigma }$ 的对角线元素是矩阵 $\mathbf{H}$ 经过排序的奇异值。 $\mathbf{H}$ 的秩等于非零奇异值的个数, 即 $\mathrm{rank}(\mathbf{H})⩽N_{\text{min }}$ 。在 $N_{\text{min }}=N_{\mathrm{Tx}}$ 的情况下，式（1）中的 SVD 也可以表示为
$$\begin{array}{rl}\mathbf{H}& =\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{H}}\\ & =\underset{\mathbf{U}}{\underbrace{[{\mathbf{U}}_{N_{\min }}{\mathbf{U}}_{N_{\mathrm{Rx}}-N_{\min }}}}]\underset{\Sigma }{\underbrace{\left[\begin{array}{c}{\Sigma }_{N_{\min }}\\ 0_{N_{\mathrm{Rx}}-N_{\min }}\end{array}\right]}}{\mathbf{V}}^{\mathrm{H}}\\ & ={\mathbf{U}}_{N_{\min }}{\mathbf{\Sigma }}_{N_{\min }}{\mathbf{V}}^{\mathrm{H}}\end{array}$$

其中, ${\mathbf{U}}_{N_{\min }}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\min }}$ 由 $N_{\min }$ 个最大非零奇异值对应的左奇异值向量构成, 且 ${\Sigma }_{N_{\min }}\in {\mathbb{C}}^{N_{\min }\times N_{\min }}$ 是方阵。由于 ${\mathbf{U}}_{N_{\mathrm{mm}}}$ 中的 $N_{\min }$ 个奇异值向量的长度为 $N_{\mathrm{Rx}}$, 所以总是存在 $N_{\mathrm{Rx}}-N_{\min }$ 个奇异值向量使得 $\left[{\mathbf{U}}_{N_{\min }}{\mathbf{U}}_{N_{\mathrm{kx}}-N_{\min }}\right]$ 是酉矩阵。

在 $N_{\min }=N_{\mathrm{Rx}}$ 的情况下, 式 (1) 中的 SVD 可以表示为
$$\begin{array}{rl}\mathbf{H}& =\mathbf{U}\underset{\mathbf{\Sigma }}{\underbrace{[{\mathbf{\Sigma }}_{N_{\min }}{0}_{N_{\mathrm{Ta}}-N_{\mathrm{mix}}}}}]\underset{{\mathbf{V}}^{\mathrm{H}}}{\underbrace{\left[\begin{array}{c}{\mathbf{V}}_{N_{\mathrm{mix}}}^{\mathrm{H}}\\ {\mathbf{V}}_{N_{\mathrm{Tx}}}^{\mathrm{H}}-N_{\mathrm{man}}\end{array}\right]}}\\ & =\mathbf{U}{\mathbf{\Sigma }}_{N_{\mathrm{mix}}}{\mathbf{V}}_{N_{\min }}^{\mathrm{H}}\end{array}$$
其中, $V_{N_{\min }}\in {\mathbb{C}}^{N_{\mathrm{T}}\times N_{\min }}$ 由 $N_{\min }$ 个右奇异值向量构成。

给定 $\mathbf{H}$ 的 SVD, 以下的特征值分解成立:
$$\begin{array}{c}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}=\mathbf{U}\Sigma {\Sigma }^{\mathrm{H}}{\mathbf{U}}^{\mathrm{H}}=\mathbf{QA}{\mathbf{Q}}^{\mathrm{H}}\end{array}$$

其中, $\mathbf{Q}=\mathbf{U}$, 满足 ${\mathbf{Q}}^{\mathrm{H}}\mathbf{Q}={\mathbf{I}}_{N_{\mathrm{zx}}}$, 且 $\mathbf{A}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{Rx}}}$ 是对角矩阵, 其对角元素为
$$\begin{array}{c}{\lambda }_i=\{\begin{array}{ll}{\sigma }_i^2,& i=1,2,\cdots ,N_{\text{min }}\\ 0,& i=N_{\text{min }}+1,\cdots ,N_{\mathrm{Rx}}\end{array}\end{array}$$

因为 $\mathbf{A}$ 的对角元素是特征值 { λ i } i = 1 N R x \left\{\lambda_i\right\}_{i=1}^{N_{\mathrm{Rx}}} {λi​}i=1NRx​​, 所以式 (5) 说明 $\mathbf{H}$ 的奇异值的平方 $\left\{{\sigma }_i^2\right\}$ 是埃米特对称矩阵 $\mathbf{H}{\mathbf{H}}^{\mathrm{H}}$ 或 ${\mathbf{H}}^{\mathrm{H}}\mathbf{H}$ 的特征值。所以，我们可以通过计算矩阵 $\mathbf{H}{\mathbf{H}}^{\mathrm{H}}$ 或 ${\mathbf{H}}^{\mathrm{H}}\mathbf{H}$ 的特征值来获得矩阵 $\mathbf{H}$ 的奇异值。

$$\begin{array}{c}\text{Tr}(\mathbf{H}{\mathbf{H}}^{\mathrm{H}})=\sum _i{\sigma }_i^2\end{array}$$
这个等式揭示了信道的能量与其奇异值之间的直接联系：信道的总能量可以通过其奇异值的平方和来确定。这对于理解和分析信道的特性非常有用，因为奇异值本身就提供了信道能够传输信息的“能力”或“强度”的度量。

对于一个非埃米特方阵 $\mathbf{H}\in {\mathbb{C}}^{n\times n}$ (或非对称实矩阵), 其特征值分解可表示为

$$\begin{array}{c}\mathbf{H}=\mathbf{X}{\mathbf{A}}_{\mathrm{nan}-H}{\mathbf{X}}^{-1}\end{array}$$

其中, { x i } i = 1 n ∈ C n × 1 \left\{\boldsymbol{x}_i\right\}_{i=1}^n \in \mathbb{C}^{n \times 1} {xi​}i=1n​∈Cn×1 为 ${\mathbf{A}}_{\mathrm{non}-H}\in {\mathbb{C}}^{n\times n}$ 中特征值对应的右特征值向量。在式 (7) 中, 假设特征值向量是线性无关的。比较式 (4) 和式 (7), 很容易看出非埃米特矩阵 $\mathbf{H}\in {\mathbb{C}}^{n\times n}$ 的特征值向量不是正交的, 而埃米特矩阵 $\mathbf{H}{\mathbf{H}}^{\mathrm{H}}$ 的特征值向量是正交的, 即 ${\mathbf{Q}}^{-1}={\mathbf{Q}}^{\mathrm{H}}$ 。
此外, MIMO 信道的 Frobenius 范数的平方被认为是信道增益的总功率, 即
$$\begin{array}{c}\Vert \mathbf{H}{\Vert }_{\mathrm{F}}^2=\mathrm{Tr}\left(\mathbf{H}{\mathbf{H}}^{\mathrm{H}}\right)=\sum _{i=1}^{N_{\mathrm{Rx}}}\sum _{j=1}^{N_{\mathrm{Tx}}}|h_{i,j}{|}^2\end{array}$$

利用式 (4) 中的特征值分解, 式 (8) 可以表示为
$$\begin{array}{rl}\Vert \mathbf{H}{\Vert }_{\mathrm{F}}^2& ={\Vert {\mathbf{Q}}^{\mathrm{H}}\mathbf{H}\Vert }_{\mathrm{F}}^2\\ & =\mathrm{Tr}\left({\mathbf{Q}}^{\mathrm{H}}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}\mathbf{Q}\right)\\ & =\mathrm{Tr}\left({\mathbf{Q}}^{\mathrm{H}}\mathbf{Q}\mathbf{A}{\mathbf{Q}}^{\mathrm{H}}\mathbf{Q}\right)\\ & =\mathrm{Tr}(\mathbf{A})\text{(对角线元素之和)}\\ & =\sum _{i=1}^{N_{\min }}{\lambda }_i\\ & =\sum _{i=1}^{N_{\min }}{\sigma }_i^2\end{array}$$
在推导式（9）的过程中用到了：与酉矩阵相乘，矩阵的Frobenius范数保持不变。

2. 确定性MIMO信道容量

对于 $N_{\mathrm{Tx}}$ 根发射天线和 $N_{\mathrm{Rx}}$ 根接收天线的 $\mathrm{MIMO}$ 系统，时不变窄带无线信道可以表示成 $N_{\mathrm{Rx}}\times N_{\mathrm{Tx}}$ 的确定性矩阵 $\mathbf{H}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times N_{\mathrm{Tx}}}$ 。对于由 $N_T$ 个独立符号 $x_1,x_1,\cdots ,x_{N_{\mathrm{Tx}}}$ 构成的发射符号向量 $\mathbf{x}\in {\mathbb{C}}^{N_{\mathrm{Tx}}\times 1}$, 接收信号 $\mathbf{y}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times 1}$ 可以表示为
$$\begin{array}{c}\mathbf{y}=\sqrt{\frac{E_x}{N_{\mathrm{Tx}}}}\mathbf{H}\mathbf{x}+\mathbf{z}\end{array}$$

其中, $z={\left(z_1,z_1,\cdots ,z_{N_{\mathrm{Rx}}}\right)}^{\mathrm{T}}\in {\mathbb{C}}^{N_R\times 1}$ 是噪声向量, 假设服从零均值循环对称复高斯 (Zero Mean Circular Symmetric Complex Gaussian, ZMCSCG）分布。对于任意的 $\theta$, 当 ${\mathrm{e}}^{\mathrm{j}\theta }z$ 与 $z$ 具有相同的分布时,向量 $z$ 被称为是循环对称的。发送信号向量的自相关矩阵定义为
$$\begin{array}{c}{\mathbf{R}}_{xx}=E\left\{\mathbf{x}{\mathbf{x}}^{\mathrm{H}}\right\}\end{array}$$

当假设每一根发射天线的发射功率为 1 时, 有 $\mathrm{Tr}\left({\mathbf{R}}_{xx}\right)=N_{\mathrm{Tx}}$ 。

2.1 发射端已知CSI时的信道容量

互信息（Mutual Information，MI）度量了了解一个随机变量 $X$ 对另一个随机变量 $Y$ 的不确定性减少了多少，反之亦然。
互信息衡量的是通过观察一个随机变量可以获得的关于另一个随机变量的信息量。
数学上，两个随机变量 $X$ 和 $Y$ 之间的互信息定义为：

$$I(X;Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\log \left(\frac{p(x,y)}{p(x)p(y)}\right),$$

其中

• $p(x,y)$ 是 $X$ 和 $Y$ 的联合概率分布，
• $p(x)$ 和 $p(y)$ 分别是 $X$ 和 $Y$ 的边缘概率分布，
• 对数可以是自然对数或以 2 为底的对数，依赖于信息量的单位（比特或奈特）。

互信息可以表示为条件熵的差值：

$$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X),$$
其中

• $H(X)$ 和 $H(Y)$ 分别是 $X$ 和 $Y$ 的熵，
• $H(X|Y)$ 和 $H(Y|X)$ 分别是给定 $Y$ 的条件下 $X$ 的条件熵，和给定 $X$ 的条件下 $Y$ 的条件熵。

---

确定性信道的容量被定义为
$$\begin{array}{c}C=\underset{f(\mathbf{x})}{\max }I(\mathbf{x};\mathbf{y})\end{array}$$

其中, $f(x)$ 为发射信号向量 $\mathbf{x}$ 的 PDF, $I(\mathbf{x};\mathbf{y})$ 为随机向量 $\mathbf{x}$ 和 $\mathbf{y}$ 的互信息。通过改变发射信号向量 PDF 得到的最大互信息就是信道容量。根据信息论的基本原理, 两个连续随机向量 $\mathbf{x}$ 和 $\mathbf{y}$ 的互信息为(收到 $\mathrm{y}$ 获得关于 $\mathrm{x}$ 的信息量)
$$\begin{array}{c}I(\mathbf{x};\mathbf{y})=H(\mathbf{y})-H(\mathbf{y}\mid \mathbf{x})\end{array}$$

其中, $H(\mathbf{y})$ 为 $\mathbf{y}$ 的微分熵, $H(\mathbf{y}\mid \mathbf{x})$ 为当 $\mathbf{x}$ 给定时 $\mathbf{y}$ 的条件微分熵。

利用上式中两个随机向量 $\mathbf{z}$ 和 $\mathbf{x}$ 之间的统计独立性, 可以得到如下关系:
$$\begin{array}{c}H(\mathbf{y}\mid \mathbf{x})=H(\mathbf{z})\end{array}$$

利用式 $(14)$, 可以将式 $(13)$ 表示为
$$\begin{array}{c}I(\mathbf{x};\mathbf{y})=H(\mathbf{y})-H(\mathbf{z})\end{array}$$

从式 (15) 中可以看出如果 $H(\mathbf{z})$ 为一常数, 那么当 $H(\mathbf{y})$ 达到最大时实现互信息最大化。此外, 根据式 $(10),\mathbf{y}$ 的自相关矩阵(无干扰模式)为
$$\begin{array}{rl}{\mathbf{R}}_{\mathbf{y}\mathbf{y}}& =E\left\{\mathbf{y}{\mathbf{y}}^{\mathrm{H}}\right\}=E\left\{\left(\sqrt{\frac{E_x}{N_{\mathrm{Tx}}}}\mathbf{H}\mathbf{x}+\mathbf{z}\right)\left(\sqrt{\frac{E_x}{N_{\mathrm{Tx}}}}{\mathbf{x}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}+{\mathbf{z}}^{\mathrm{H}}\right)\right\}\\ & =E\left\{\left(\frac{E_x}{N_{\mathrm{Tx}}}\mathbf{H}\mathbf{x}{\mathbf{x}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}+\mathbf{z}{\mathbf{z}}^{\mathrm{H}}\right)\right\}\text{噪声是独立的，所以噪声和发送信号的交叉项的期望是零}\\ & =\frac{E_x}{N_{\mathrm{Tx}}}E\left\{\mathbf{H}\mathbf{x}{\mathbf{x}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}+\mathbf{z}{\mathbf{z}}^{\mathrm{H}}\right\}\\ & =\frac{E_x}{N_{\mathrm{Tx}}}\mathbf{H}E\left\{\mathbf{x}{\mathbf{x}}^{\mathrm{H}}\right\}{\mathbf{H}}^{\mathrm{H}}+E\left\{\mathbf{z}{\mathbf{z}}^{\mathrm{H}}\right\}\\ & =\frac{E_x}{N_{\mathrm{Tx}}}\mathbf{H}{\mathbf{R}}_{xx}{\mathbf{H}}^{\mathrm{H}}+N_0{\mathbf{I}}_{N_{\mathrm{Rx}}}\end{array}$$

其中, $E_x$ 为发射信号的能量, $N_0$ 为加性噪声 { z i } i = 1 N R x \left\{z_i\right\}_{i=1}^{N_{\mathrm{Rx}}} {zi​}i=1NRx​​ 的功率谱密度。当 $\mathbf{y}$ 为 ZMCSCG 向量时, 微分摘 $H(y)$ 最大, 因此要求 $\mathbf{x}$ 也是 ZMCSCG 向量。 $\mathbf{y}$ 和 $z$ 的互信息分别为
H ( y ) = log ⁡ 2 { det ⁡ ( π e R y y ) } H ( z ) = log ⁡ 2 { det ⁡ ( π e N 0 I N R x ) } \begin{align} & H(\boldsymbol{y})=\log _2\left\{\operatorname{det}\left(\pi \mathrm{e} \boldsymbol{R}_{y y}\right)\right\}\notag \\ & H(\boldsymbol{z})=\log _2\left\{\operatorname{det}\left(\pi \mathrm{e} N_0 \boldsymbol{I}_{N_{\mathrm{Rx}}}\right)\right\} \end{align} ​H(y)=log2​{det(πeRyy​)}H(z)=log2​{det(πeN0​INRx​​)}​​

在文献[217]中, 已经证明了利用式 (17)，式 (15) 中的互信息可以表示为
$$\begin{array}{c}I(\mathbf{x};\mathbf{y})={\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\mathbf{HR}}_{xx}{\mathbf{H}}^{\mathrm{H}}\right)\mathrm{bps}/\mathrm{Hz}\end{array}$$

确定性 MIMO 信道的容量可以表示为（只有$\mathbf{x}$是未知变量）
$$\begin{array}{c}C=\underset{\mathrm{Tr}\left(R_{xx}\right)=N_{\mathrm{Tx}}}{\max }{\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}\mathbf{H}{\mathbf{R}}_{xx}{\mathbf{H}}^{\mathrm{H}}\right)\text{ bps }/\mathrm{Hz}\end{array}$$

图1：发射端可以获得CSI时的模态分解

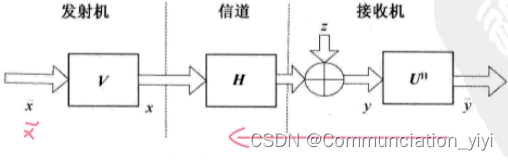
如图1所示, 当发射端已知信道状态信息 (Channel State Information, CSI) 时, 执行模态分解, 在发射机用 $\mathbf{V}$ 预处理发射信号, 然后在接收机用 ${\mathbf{U}}^{\mathrm{H}}$ 后处理接收信号。

根据图1，接收机的输出信号可以表示为
$$\begin{array}{c}\tilde{\mathbf{y}}=\sqrt{\frac{E_x}{N_{T_x}}}{\mathbf{U}}^{\mathrm{H}}\mathbf{H}\mathbf{V}\tilde{\mathbf{x}}+\tilde{\mathbf{z}}\end{array}$$
其中，$\tilde{\mathbf{z}}={\mathbf{U}}^{\mathrm{H}}\mathbf{z}$。利用式（1）中的奇异值分解，式（20）可以重写为
$$\begin{array}{c}\tilde{\mathbf{y}}=\sqrt{\frac{E_x}{N_{\mathrm{Tr}}}}\mathbf{\Sigma }\tilde{\mathbf{x}}+\tilde{\mathbf{z}}\end{array}$$
$$\begin{array}{c}{\tilde{y}}_i=\sqrt{\frac{E_i}{N_{\mathrm{Tx}}}}\sqrt{{\lambda }_i}{\tilde{x}}_i+{\tilde{z}}_j,i=1,2,\cdots ,r\end{array}$$
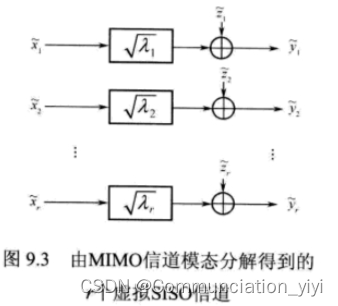
上面的等价表达式可由图 2来说明。如果第 $i$ 根发射天线的发射功率为 ${\gamma }_i=E\left\{{\left|x_i\right|}^2\right\}$, 那么第 $i$ 个虚拟的 SISO 信道容量为
$$\begin{array}{c}{C}_i\left({\gamma }_i\right)={\log }_2\left(1+\frac{E_x{\gamma }_i}{N_{\mathrm{Tx}}{N}_0}{\lambda }_i\right),i=1,2,\cdots ,r\end{array}$$

图2：由MIMO信道模态分解的得到的虚拟SISO信道

假设发射机可用的总功率为
$$\begin{array}{c}E\left\{{\mathbf{x}}^{\mathrm{H}}\mathbf{x}\right\}=\sum _{i=1}^{N_{\mathrm{Tx}}}E\left\{{\left|x_i\right|}^2\right\}\end{array}$$

此时，MIMO 信道容量是所有虚拟 SISO 信道容量之和，即
$$C=\sum _{i=1}^r{C}_i\left({\gamma }_i\right)=\sum _{i=1}^r{\log }_2\left(1+\frac{E_x{\gamma }_i}{N_{\mathrm{Tx}}{N}_0}{\lambda }_i\right)$$

式 (24) 必须满足式 (23) 中的总功率约束。通过求解下面的功率分配问题, 能够得到式 (24)中的最大容量:
C = max ⁡ { γ i } ∑ i = 1 r log ⁡ 2 ( 1 + E x γ i N T x N 0 λ i )  s.t.  ∑ i = 1 r γ i = N T x \begin{align} & C=\max _{\left\{\gamma_i\right\}} \sum_{i=1}^r \log _2\left(1+\frac{E_x \gamma_i}{N_{\mathrm{Tx}} N_0} \lambda_i\right) \notag\\ & \text { s.t. } \sum_{i=1}^r \gamma_i=N_{\mathrm{Tx}} \end{align} ​C={γi​}max​i=1∑r​log2​(1+NTx​N0​Ex​γi​​λi​) s.t. i=1∑r​γi​=NTx​​​

可以证明式 (25) 中的最优化问题的解为
$$\begin{array}{c}{\gamma }_i^{\mathrm{opt}}={\left(\mu -\frac{N_{\mathrm{Tx}}{N}_0}{E_x{\lambda }_i}\right)}^{+},i=1,\cdots ,r\\ \sum _{i=1}^r{\gamma }_i^{\mathrm{opt}}=N_{\mathrm{Tx}}\end{array}$$

其中, $\mu$ 是一个常数, $(x{)}^{+}$被定义为
$$\begin{array}{c}(x{)}^{+}=\{\begin{array}{cc}x,& x⩾0\\ 0,& x<0\end{array}\end{array}$$

当满足式 (27) 的约束条件时，式 (26) 的解可由著名的注水功率算法得到。如图 3 所示，注水算法给更高的 SNR 模式分配更多的功率。如果模式的 SNR 低于给定门限 $\mu$，则该模式不能被使用，即不给该模式分配功率。

输入: λ[1...r] (通道增益), N_Tx (总传输功率), N_0 (噪声功率), E_x

1. 初始化:
    γ[1...r] = 0
    μ = 无穷大

2. 将λ排序为降序，得到排序后的索引order

3. 为每个通道i进行注水:
   for i = 1 to r do
       μ_temp = (N_Tx + sum(N_0 / (λ[order[1:i]] * E_x))) / i
       if μ_temp < μ then
           μ = μ_temp
       end if
   end for

4. 计算每个通道的功率分配:
   for i = 1 to r do
       γ[i] = max(μ - (N_Tx * N_0) / (E_x * λ[i]), 0)
   end for

5. 确保总功率约束:
   if sum(γ[1...r]) ≠ N_Tx then
       print "Error in power allocation!"
       return
   end if

6. 计算总容量:
   C = 0
   for i = 1 to r do
       C = C + log2(1 + (E_x * γ[i] / (N_Tx * N_0)) * λ[i])
   end for

输出: C, γ[1...r]

2.2 发射端位置CSI时的信道容量

当发射机不能获得CSI时，总功率平均分配给所有的发射天线。
此时，发射信号向量$\mathbf{x}$的自相关函数为
$$\begin{array}{c}{\mathbf{R}}_{xx}={\mathbf{I}}_{xx}\end{array}$$
在这种情况下, 信道容量可以表示为
$$\begin{array}{c}C={\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{TX}}{N}_0}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}\right)\end{array}$$

利用特征值分解 $\mathbf{H}{\mathbf{H}}^{\mathrm{H}}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{H}}$ 和恒等式 $\det \left({\mathbf{I}}_m+\mathbf{AB}\right)=\det \left({\mathbf{I}}_n+\mathbf{B}\mathbf{A}\right)$, 其中 $\mathbf{A}\in {\mathbb{C}}^{m\times n}$ 和 $\mathbf{B}\in {\mathbb{C}}^{n\times m}$，式 (30) 中的信道容量可以表示为
$$\begin{array}{rl}C& ={\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}\underset{\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{H}}\mathbf{Q}}{\underbrace{\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{H}}}}\right)\\ & ={\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}\mathbf{\Lambda }\right)\\ & =\sum _{i=1}^r{\log }_2\left(1+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\lambda }_i\right)\end{array}$$

其中, $r$ 为 $\mathbf{H}$ 的秩, 即 $r=N_{\min }\triangleq \min \left(N_{Tx},N_{\mathrm{Rx}}\right)$。从式 (31) 中可以看出, MIMO 信道转换为 $r$个虚拟的 SISO 信道，每个信道的发射功率为 $E_x/N_{\mathrm{Tx}}$, 并且第 $i$ 个 SISO 信道的增益为 ${\lambda }_i$。注意，式 (31) 是式 (24) 在 ${\gamma }_i=1,i=1,2,\cdots ,r$ 特殊情况下的结果。

如果总的信道增益是固定不变的, 如 $\Vert \mathbf{H}{\Vert }_{\mathrm{F}}^2={\sum }_{i=1}^r{\lambda }_i=\zeta$，$\mathbf{H}$ 是满秩的, $N_{\mathrm{Tx}}=N_{\mathrm{Rx}}=N$, $r=N$，那么，当所有并行的 SISO 信道拥有相同的奇异值时，式 (31) 的信道容量达到最大。也就是说，SISO 信道的奇异值为
$$\begin{array}{c}{\lambda }_i=\frac{\zeta }{N},i=1,2,\cdots ,N\end{array}$$

式 (32) 说明当信道正交时 MIMO 信道容量达到最大, 即信道具有如下特征:
$$\begin{array}{c}{\mathbf{HH}}^{\mathrm{H}}={\mathbf{H}}^{\mathrm{H}}\mathbf{H}=\frac{\zeta }{N}{\mathbf{I}}_N\end{array}$$

式 (33) 使得 MIMO 信道容量是每个并行信道容量的 $N$ 倍, 即
$$\begin{array}{c}C=N{\log }_2\left(1+\frac{\zeta E_x}{N_{0}N}\right)\end{array}$$

2.3 SIMO信道容量

对于具有一根发射天线、 $N_{\mathrm{Rx}}$ 根接收天线的 SIMO 信道, 信道增益为 $\mathbf{h}\in {\mathbb{C}}^{N_{\mathrm{Rx}}\times 1}$，因此 $r=1$，${\lambda }_1=\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2$ 。不论发射机已知或者未知 CSI，信道容量都为
$$\begin{array}{c}{C}_{\text{SIMO }}={\log }_2\left(1+\frac{E_x}{N_0}\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2\right)\end{array}$$

如果 ${\left|h_i\right|}^2=1,i=1,2,\cdots ,N_{\mathrm{Rx}}$，有 $\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2=N_{\mathrm{Rx}}$，那么式 (35) 中的容量可以表示为
$$\begin{array}{c}{C}_{\text{SIMO }}={\log }_2\left(1+\frac{E_x}{N_0}{N}_{\mathrm{Rx}}\right)\end{array}$$

从式 (36) 中可以看出，信道容量随天线数量对数增加；此外，只能发射一个数据流，且发射机对 CSI 的获取根本不能改善信道容量。

2.4 MISO信道容量

在 MISO 信道下, 信道增益为 $\mathbf{h}\in {\mathbb{C}}^{1\times N_{\mathrm{Tx}}}$，因此 $r=1,{\lambda }_1=\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2$ 。当发射机未知 CSI 时，信道容量为
$$\begin{array}{c}{C}_{\text{MISO }}={\log }_2\left(1+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2\right)\end{array}$$

如果 ${\left|h_i\right|}^2=1,i=1,2,\cdots ,N_{\mathrm{Tx}}$，有 $\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2=N_{\mathrm{Tx}}$，那么式 (37) 简化为
$$\begin{array}{c}{C}_{\text{MISO }}={\log }_2\left(1+\frac{E_x}{N_0}\right)(当发射机未知CSI时)\end{array}$$

从式 (38) 中可以看出, MISO 信道容量与 SISO 信道容量相同。人们可能会问：当与单发射天线系统的容量相同时，多发射天线系统的优势是什么? 尽管两个系统能够获得相同的最大传输速率，但是有多种方法利用多天线。例如，空时编码技术可以提高传输的可靠性。

当发射机可以获得 CSI ( $\mathbf{h}$ 已知) 时, 可以把发射功率集中于当前信道的某个特定模式。换句话说，发射 $\left({\mathbf{h}}^{\mathrm{H}}/\Vert \mathbf{h}\Vert \right)x$ 而不是直接发射 $x$ 。接收信号可以表示为
$$\begin{array}{c}y=\sqrt{E_x}\mathbf{h}\cdot \frac{{\mathbf{h}}^{\mathrm{H}}}{\Vert \mathbf{h}\Vert }x+\mathbf{z}=\sqrt{E_x}\Vert \mathbf{h}\Vert x+\mathbf{z}\end{array}$$

式 (39) 中接收信号的功率提高了 $N_{\mathrm{Tx}}$ 倍, 因此信道容量为
$$\begin{array}{c}{C}_{\mathrm{MISO}}={\log }_2\left(1+\frac{E_x}{N_0}\Vert \mathbf{h}{\Vert }_{\mathrm{F}}^2\right)={\log }_2\left(1+\frac{E_x}{N_0}{N}_{\mathrm{Tx}}\right)\end{array}$$

3. 随机MIMO信道容量

MIMO 信道通常是随机变化的, 因此 $\mathbf{H}$ 是随机矩阵，这意味着 MIMO 信道的容量也是随机时变的。换句话说，MIMO 信道的容量可以通过它的时间平均给出。在实际中，假设随机信道是遍历¹过程。然后, 考虑 MIMO 信道容量的统计概念：
C ˉ = E { C ( H ) } = E { max ⁡ Tr ⁡ ( R x x ) = N T x log ⁡ 2 det ⁡ ( I N R x + E x N T x N 0 H R x x H H ) } \begin{align} \bar{C}&=E\{C(\boldsymbol{H})\}\notag\\ &=E\left\{\max _{\operatorname{Tr}\left(\boldsymbol{R}_{x x}\right)=N_{\mathrm{Tx}}} \log _2 \operatorname{det}\left(\boldsymbol{I}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}} N_0} \boldsymbol{H} \boldsymbol{R}_{x x} \boldsymbol{H}^{\mathrm{H}}\right)\right\} \end{align} Cˉ​=E{C(H)}=E{Tr(Rxx​)=NTx​max​log2​det(INRx​​+NTx​N0​Ex​​HRxx​HH)}​​
$\bar{C}$ 通常被称为遍历信道容量。例如，对于发射机未知 CSI 的开环系统，由式 (31) 可以得到其遍历信道容量为
$$\begin{array}{c}{\bar{C}}_{\mathrm{OL}}=E\left\{\sum _{i=1}^r{\log }_2\left(1+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\lambda }_i\right)\right\}\end{array}$$

类似地, 对于发送端使用 CSI 的闭环系统，由式 (24) 可以得到其遍历信道容量为
$$\begin{array}{rl}{\bar{C}}_{\mathrm{CL}}& =E\left\{\underset{{\sum }_{i=1}^r{\gamma }_i=N_{\mathrm{Tx}}}{\max }\sum _{i=1}^r{\log }_2\left(1+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\gamma }_j{\lambda }_i\right)\right\}\\ & =E\left\{\sum _{i=1}^r{\log }_2\left(1+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\gamma }_i^{\text{opt }}{\lambda }_i\right)\right\}\end{array}$$

信道容量的另一个统计概念是信道的中断容量。中断概率定义为
$$\begin{array}{c}{P}_{\text{out }}(R)=\mathrm{Pr}(C(\mathbf{H})<R)\end{array}$$

换句话说，如果对传输速率为 $R\mathrm{bps}/\mathrm{Hz}$ 的数据，不能实现任意小的译码差错概率，那么这个系统就处于中断状态。信道的 $\epsilon$ 中断容量定义为：使式 (45) 中的中断概率小于 $\epsilon$ 的可能的最大数据速率。换句话说，信道的中断容量就是满足 $P\left(C(\mathbf{H})⩽C_{\epsilon }\right)=\epsilon$ 所对应的 $C_{\epsilon }$ 。

4. 讨论信道相关性

总的来说, MIMO 信道增益不是独立同分布的。MIMO 信道容量与信道的相关性密切相关。接下来, 考虑当发射天线和接收天线之间的信道相关时 MIMO 信道的容量。当 SNR 较高时, 确定性信道的容量可以近似为
$$\begin{array}{c}C\approx \underset{\mathrm{Tr}\left({\mathbf{R}}_{xx}\right)=N}{\max }{\log }_2\det \left({\mathbf{R}}_{xx}\right)+{\log }_2\left(\frac{E_x}{N{N}_0}{\mathbf{H}}_{\mathrm{w}}{\mathbf{H}}_{\mathrm{w}}^{\mathrm{H}}\right)\end{array}$$

可以看出式 (46) 中的第二项为常数, 而包含 $\det \left({\mathbf{R}}_{xx}\right)$ 的第一项在 ${\mathbf{R}}_{xx}={\mathbf{I}}_N$ 时最大。考虑如下的相关信道模型:
$$\begin{array}{c}\mathbf{H}={\mathbf{R}}_{\mathrm{Rx}}^{1/2}{\mathbf{H}}_{\mathrm{w}}{\mathbf{R}}_{\mathrm{Tx}}^{1/2}\end{array}$$

其中, ${\mathbf{R}}_{\mathrm{Tx}}$ 为反映发射天线之间相关性的相关矩阵 (即 $\mathbf{H}$ 的列向量之间的相关性), ${\mathbf{R}}_{\mathrm{Rx}}$ 为反映接收天线之间相关性的相关矩阵 (即 $\mathbf{H}$ 的行向量之间的相关性), ${\mathbf{H}}_{\mathrm{w}}$ 为 i.i.d. 瑞利衰落的信道增益矩阵。 ${\mathbf{R}}_{\mathrm{Tx}}$ 和 ${\mathbf{R}}_{\mathrm{Rx}}$ 的对角线元素都被限定为 1。然后, 由式 (30) 可以得到 MIMO 信道的容量为
$$\begin{array}{c}C={\log }_2\det \left({\mathbf{I}}_{N_{\mathrm{Rx}}}+\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\mathbf{R}}_{\mathrm{Rx}}^{1/2}{\mathbf{H}}_{\mathrm{w}}{\mathbf{R}}_{\mathrm{Tx}}{\mathbf{H}}_{\mathrm{w}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{Rx}}^{\mathrm{H}/2}\right)\end{array}$$

如果 $N_{\mathrm{Tx}}=N_{\mathrm{Rx}}=N,{\mathbf{R}}_{\mathrm{Tx}}$ 和 ${\mathbf{R}}_{\mathrm{Rx}}$ 是满秩的, 且 $\mathrm{SNR}$ 很高, 那么式 (48) 可近似为
$$\begin{array}{c}C\approx {\log }_2\det \left(\frac{E_x}{N_{\mathrm{Tx}}{N}_0}{\mathbf{H}}_{\mathrm{w}}{\mathbf{H}}_{\mathrm{w}}^{\mathrm{H}}\right)+{\log }_2\det \left({\mathbf{R}}_{\mathrm{Rx}}\right)+{\log }_2\det \left({\mathbf{R}}_{\mathrm{Tx}}\right)\end{array}$$

从式 (49) 中可以发现 MIMO 信道容量已经减少了。发射天线和接收天线之间的相关性使信道容量减少的数量为 (单位: bps)
$$\begin{array}{c}{\log }_2\det \left({\mathbf{R}}_{\mathrm{Rx}}\right)+{\log }_2\det \left({\mathbf{R}}_{\mathrm{Tx}}\right)\end{array}$$
可以证明对于任意的相关矩阵 $\mathbf{R}$, 有 ${\log }_2\det (\mathbf{R})⩽0$ ²。因此, 式(50)的取值总是负的。 $\mathbf{R}$是对称矩阵,因此可以使用式 (2) 中的特征值分解,即 $\mathbf{R}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\mathrm{H}}$ 。由于西矩阵的行列式为 1,所以相关矩阵的行列式可以表示为
$$\begin{array}{c}\det (\mathbf{R})=\prod _{i=1}^N{\dot{\lambda }}_i\end{array}$$

此外, 几何平均小于算数平均:
$$\begin{array}{c}{\left(\prod _{i=1}^N{\lambda }_i\right)}^{\frac{1}{N}}⩽\frac{1}{N}\sum _{i=1}^N{\lambda }_i=1\end{array}$$

从式 (51) 和式 (52) 可以更加明显地看出:
$$\begin{array}{c}{\log }_2\det (\mathbf{R})⩽0\end{array}$$

当相关矩阵是单位矩阵时, 意味着各个随机变量之间是统计独立, 式 (53) 中的等号成立。因此, 式 (50) 的结果都是负的。

---

1. 对于随机过程的所有实现来说, 如果它的时间平均收敛于相同的极限，如对于一个离散随机过程 $x[n]$，当 $N\to \infty$ 时， 1 N ∑ n = 1 N X [ n ] → E { X [ n ] } \frac{1}{N} \sum_{n=1}^N X[n] \rightarrow E\{X[n]\} N1​∑n=1N​X[n]→E{X[n]}，则称这个随机过程是遍历的。 ↩︎

2. 首先，我们知道相关矩阵$\mathbf{R}$是Hermitian的（在实数域中是对称的），且所有的主对角线元素为1（因为一个变量与自己的相关系数是1）。这意味着它是一个正半定矩阵。
   考虑到这一点，我们可以用以下方式证明给定的不等式：证明：1. 特征值：正半定矩阵的所有特征值都是非负的。因此，对于相关矩阵$\mathbf{R}$，其所有的特征值 ${\lambda }_i$ 都满足 ${\lambda }_i\ge 0$。2. 行列式与特征值的关系：一个矩阵的行列式是其所有特征值的乘积。因此，有$\det (\mathbf{R})={\prod }_{i=1}^n{\lambda }_i$其中 $n$ 是矩阵的大小。3. 由于 $0\le {\lambda }_i\le 1$（因为特征值由相关矩阵的元素决定，这些元素的范围在-1到1之间，且对角线上的元素为1），我们可以得出$0\le \det (\mathbf{R})\le 1$。 4. 取两边的 ${\log }_2$ ，我们得到${\log }_2\det (\mathbf{R})\le 0$这正是我们想要证明的。因此，对于任意的相关矩阵 $\mathbf{R}$，我们已经证明了 ${\log }_2\det (\mathbf{R})\le 0$。 ↩︎