一、74LS183简介:
74LS183是一种4位高速全加器,用于数字电路中的加法运算。74LS183输入端包括两个4位二进制数和一个进位信号,输出端包括1个4位二进制数和一个进位信号。
74LS138具有快速响应、低功耗灯特点,能实现高校的数字匀速。
二、74LS183引脚定义:

三、74LS183功能表:
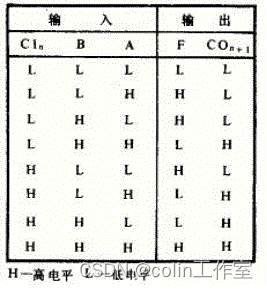
四、74LS183逻辑图:

五、仿真原理图:

六、运行效果:

一、74LS183简介:
74LS183是一种4位高速全加器,用于数字电路中的加法运算。74LS183输入端包括两个4位二进制数和一个进位信号,输出端包括1个4位二进制数和一个进位信号。
74LS138具有快速响应、低功耗灯特点,能实现高校的数字匀速。
二、74LS183引脚定义:

三、74LS183功能表:

四、74LS183逻辑图:

五、仿真原理图:

六、运行效果:

 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


