第二类生产线平衡问题及其MATLAB实现

        生产线平衡问题是经典的N-P问题, 我们常用遗传算法或粒子群算法等智能算法予以求解. 生产线平衡问题是一种有顺序约束的装配问题, 目标函数一般是工作站数量最小化或生产节拍最小化或最大化平衡率或平滑指数.

        前面的一篇文章介绍了第一类生产线平衡问题及其MATLAB实现(最小化工作站数量), 今天我们介绍第二类生产线平衡问题.

       生产线平衡问题的模型为: 有N个作业工序, 各作业工序的时间为Ti(图中圆圈上部的数字), 无回路的有向图G规定了N个工序的装配顺序约束(举例如下图所示). 图G中箭头所指为工序之间的紧前约束, 也即箭头起点的工序完成后才能开始箭头终点的工序. 第一类生产线平衡问题就是基于以上模型, 寻找一个划分, 将N个工序划分为m个有序子集(每个子集称为一个工位), 使得满足G的同时, 最小化m.

       第二类生产线平衡问题即确定了工作站数目m、任务时间Ti和工位优先顺序，使得生产节拍CT最小，数学模型如下:

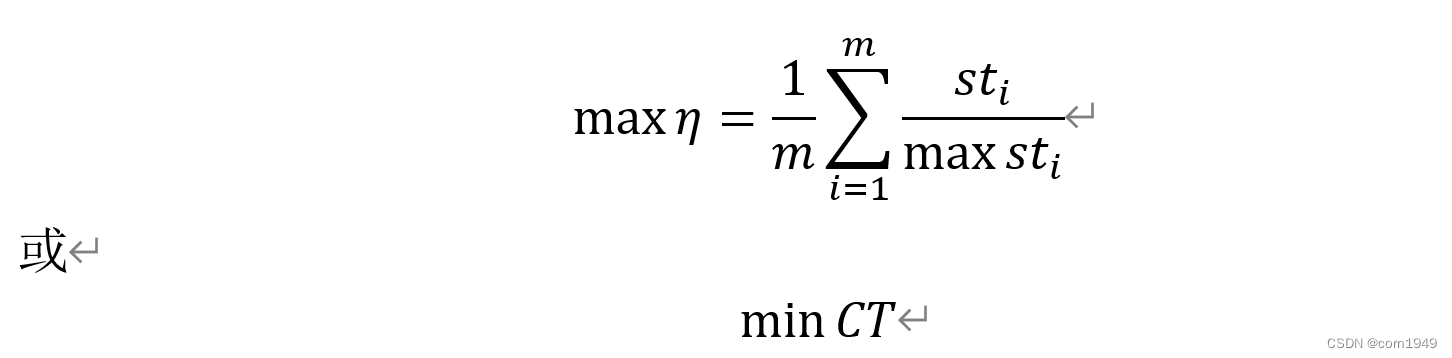
式中：η为平衡率；

sti为第i个工作站的完成工时

mi为第i个工作站中安排的工序个数

Tik为第i个工作站中第k个工序的工作时长

max(sti) 为工作站的最大完成工时间；

CT为生产节拍；

m为工作站数。

该模型的假设如下:

(1)各作业工序Ti的时间已知且是确定的。
(2)每一个作业工序不可以再分配给两个工位，且需要是不能再分割的最小作业单元。
(3)作业工序时间不超过工位的时间。
(4)作业工序中的最大时间不可以大于装配线的节拍时间
(5)装配线可以完成装配过程的每一项作业。
(6)不准许并行的工作站在装配线上同时存在。

图G 

      对以上问题, 我们可以采用经典智的能算法遗传算法来求解. 

根据图G, 我们构造以下的数据表作为程序的格式化输入数据. 并存到Excel中.

编号	工序	紧前工序	时间/min
1	工序1	0	1.2
2	工序2	1	0.8
3	工序3	1	1.9
4	工序4	1	1
5	工序5	2	0.7
6	工序6	3、4	1.1
7	工序7	5、6	2.5

       然后我们采用自然数排序编码给定一个工序的顺序, 从1到N的自然数的排序, 比如N=7时, 编码[2,3,1,4,6,5,7]表示一个染色体,代表一个装配方案. 这里非常关键的是排序编码如何对应一个装配方案, 这是关键点之一, 后面有时间专门出一期论述. 

MATLAB实现代码如下:

%% 遗传算法
clc;close all;clear all;warning off;%清除变量
rand('seed', 500);
randn('seed', 300);
format long g;
addpath(genpath('gatoolbox'));
%% 本代码由华量信息技术工作室 代码顾问免费提供 联系方式 QQ1579325979

global T stationnumber0 nodenumber premat;
global w1 w2;

%% 设置模型参数
w1=0.5;
w2=0.5;

%% 读取数据
filename_my='数据.xls';
[adata201_my,bdata201_my,cdata201_my]=xlsread(filename_my);

T=adata201_my(:,4);
beforecdata_my=cdata201_my(2:end,3);
n_my=size(beforecdata_my,1);
premat=prematfun(beforecdata_my);

nodenumber=size(premat,1);% 工序数
stationnumber0=3;% 设定工作站数

% 设定每个工作站的可安排工序个数的范围
lb_my=max(max(T),sum(T)/stationnumber0);
ub_my=max(max(T),sum(T)/stationnumber0*2);
N_my=nodenumber;

% 遗传算法参数
popsize=50;% 遗传算法子群的种群数
maxgen=100;% 遗传算法迭代次数
PM=0.1;% 变异概率
PC=0.8;% 交叉概率

%% 遗传算法主程序
tracemat_ga_my=zeros(maxgen,2);% 性能跟踪
gen=0;
tic;
Chrom=genChrome(popsize,nodenumber,lb_my,ub_my);% 建立种群
Value=decodingFun(Chrom,popsize);% 解码染色体

while gen<maxgen
    %% 遗传算子
    FitnV=ranking(Value);% 分配适应度值
    Chrom=select('rws',Chrom,FitnV,1);% 选择
    Chrom=mutationGA(Chrom,popsize,PM,nodenumber,lb_my,ub_my);% 种群变异,单点变异
    Chrom=crossGA(Chrom,popsize,PC,nodenumber);% 种群交叉,2点交叉
    Value=decodingFun(Chrom,popsize);% 解码染色体
    
    %% 计算最优
    [vmin,indexmin]=min(Value);
    gen=gen+1;
    tracemat_ga_my(gen,2)=mean(Value);
    %% 记录最优
    if gen==1
        bestChrom_ga_my=Chrom(indexmin,:);%记录最优染色体
        bestValue_ga_my=vmin;%记录的最优值
    end
    if bestValue_ga_my>vmin
        bestChrom_ga_my=Chrom(indexmin,:);%记录最优染色体
        bestValue_ga_my=vmin;%记录的最优值
    end
    tracemat_ga_my(gen,1)=bestValue_ga_my;% 保留最优
    waitbar(gen/maxgen,wait_hand);%每循环一次更新一次进步条
end
delete(wait_hand);%执行完后删除该进度条

disp('遗传算法运行时间');
runtime_ga=toc

% 显示结果
disp('遗传算法优化得到的最优目标函数值');
bestValue_ga_my
disp('遗传算法优化得到的最优染色体');
bestChrom_ga_my

% 绘图
figure;
plot(1./tracemat_ga_my(:,1)*100,'r-','linewidth',1.5);
xlabel('迭代次数','fontname','宋体');
ylabel('平衡率(%)','fontname','宋体');
title('遗传算法迭代曲线','fontname','宋体');

% 转换为需要的格式和输出文件
x=bestChrom_ga_my;
[y,P,CT,CTmat,stationnumber,Rcell,f1,punish201]=myfun(x);
CT,punish201
stationnumber

title201='遗传算法优化得到的均衡图';
drawBalancedfun(Rcell,stationnumber,T,title201);


%% 本代码由华量信息技术工作室 代码顾问免费提供 联系方式 QQ1579325979


rmpath(genpath('gatoolbox'));

       子程序比较多, 解码函数约100行, 逻辑复杂, 基本逻辑就是人脑排工序顺序的步骤, 其他为遗传算法的变异,交叉,选择函数.

程序结果如下:

 平衡率95.8%