这里简要介绍一下如何使用最大似然估计方法来拟合威布尔分布:
- 假设样本数据x1,x2,…,xn来自于一个未知的威布尔分布。威布尔分布的概率密度函数为:
f(x|λ) = λe^(-λx)
其中λ为位置参数。
- 根据最大似然原理,我们要找到使样本数据的似然函数L(λ|x1,x2,…,xn)达到最大值的λ值。
L(λ|x1,x2,…,xn) = Πi=1^n f(xi|λ) = λ^n e^(-λΣxi)
- 对数似然函数为:
l(λ|x1,x2,…,xn) = nlogλ - λΣxi
- 将对数似然函数对λ求导并令导数为0,可以得到最大似然估计λˆ的值:
λˆ = Σxi / n
也就是样本数据的平均值。
- 所以,通过最大似然估计,我们可以得到威布尔分布位置参数λ的一个无偏估计λˆ,它等于样本数据的平均值。
以上就是利用最大似然估计方法拟合威布尔分布的基本步骤。
数据如下:
4.5601436443429
7.62862412532937
6.10435481521625
5.17911106734894
4.53737502238713
6.01159516400874
7.41074637210801
11.822337714548
10.6466358831609
10.3378228536724
1.49264705542417
6.68282534527858
13.4671284422267
9.66667276322504
3.96926844138616
3.28811058517436
6.45949731670622
12.8306267221037
4.76112071515054
2.94354705173048
8.65132829053067
4.07025852552667
5.41991945158543
7.93293700057303
2.36889275928023
7.27443698731837
7.95076274238595
8.06190901454078
9.90466610901846
6.41795399916641
7.85245829421285
8.36368464881367
4.26873223607297
10.3506021419208
5.3360985789564
6.27395246057449
6.75442746358506
9.28969851350674
3.98912407718702
0.745428231041202
3.59930760169802
4.82336229251733
8.46995737552821
5.68611753138303
5.63112152665565
5.13626846700053
9.78592420862787
4.38343275573315
16.6467377162442
6.09148864758909
3.94839868888265
8.14842107079688
5.42857013945754
2.02140997037051
7.28433324294674
12.7679286296203
6.97923009798084
9.94990051100038
6.82719535455114
3.53516340883958
12.9153889330274
5.34323305230609
5.11482377176055
5.06156634306467
19.3370910368456
11.4511291520224
4.70003057516638
5.29152519681062
6.19025264758849
9.25848484451243
8.48214945946961
9.57831745130914
19.0414835098518
2.88357835786613
6.12318980254731
7.24279148152443
2.66201388600265
7.36494731845442
9.56250988878509
11.8601704165236
3.78354849644309
5.35899541881499
16.5205727124694
3.56742702702706
2.53120985898255
10.1235179869659
6.11685828736108
5.2102854774718
6.23597712401358
4.33425039655978
4.88217129585998
6.97510387777615
7.08559632969083
1.33640194541483
4.31481960035607
8.47092426294821
8.04874230348502
6.86822229870322
10.8957538419381
3.30981412183682
程序如下:
clc;close all;clear all;warning off;%清除变量
y=wblrnd(8,2,100,1)+1*rand(100,1);% 随机数
y
x0=[1,1];
[parmhat1,ML]=fminsearch(@(x) myfun(y,x),x0);
disp('最大似然估计风速得到的威布尔分布参数');
parmhat1
ywbl=wblrnd(parmhat1(1),parmhat1(2),length(y),1);
figure;
plot(ywbl,'b-');
title('威布尔分布','fontname','宋体');
figure;
wblplot(y);
title('威布尔分布概率图','fontname','宋体');
figure; probplot('weibull',y);
a1=wblcdf(sort(y),parmhat1(1),parmhat1(2));
[counts,centers]=hist(y,100);
a0=counts/sum(counts);
g=cumsum(a0);
figure;
bar(centers,counts/sum(counts)); %画出概率密度分布图
figure;
plot(centers,g,'b*'); %画出概率密度分布图
hold on;
plot(sort(y),a1,'r');
legend({'样本','拟合'},'fontname','宋体');
xlabel('数值','fontname','宋体');
ylabel('累积概率','fontname','宋体');
title('威尔分布累积概率','fontname','宋体');
function y=myfun(data,x)
a=x(1);% 分布的参数1
b=x(2);% 分布的参数2
% y = wblpdf(data,A,B);% 概率
p=b/a*(data/a).^(b-1).*exp(-(data/a).^b);% 威布尔分布的概率密度函数
y=-sum(log(p));% 似然函数值最大化
程序结果如下:
最大似然估计风速得到的威布尔分布参数
parmhat1 =
8.1692 2.0760
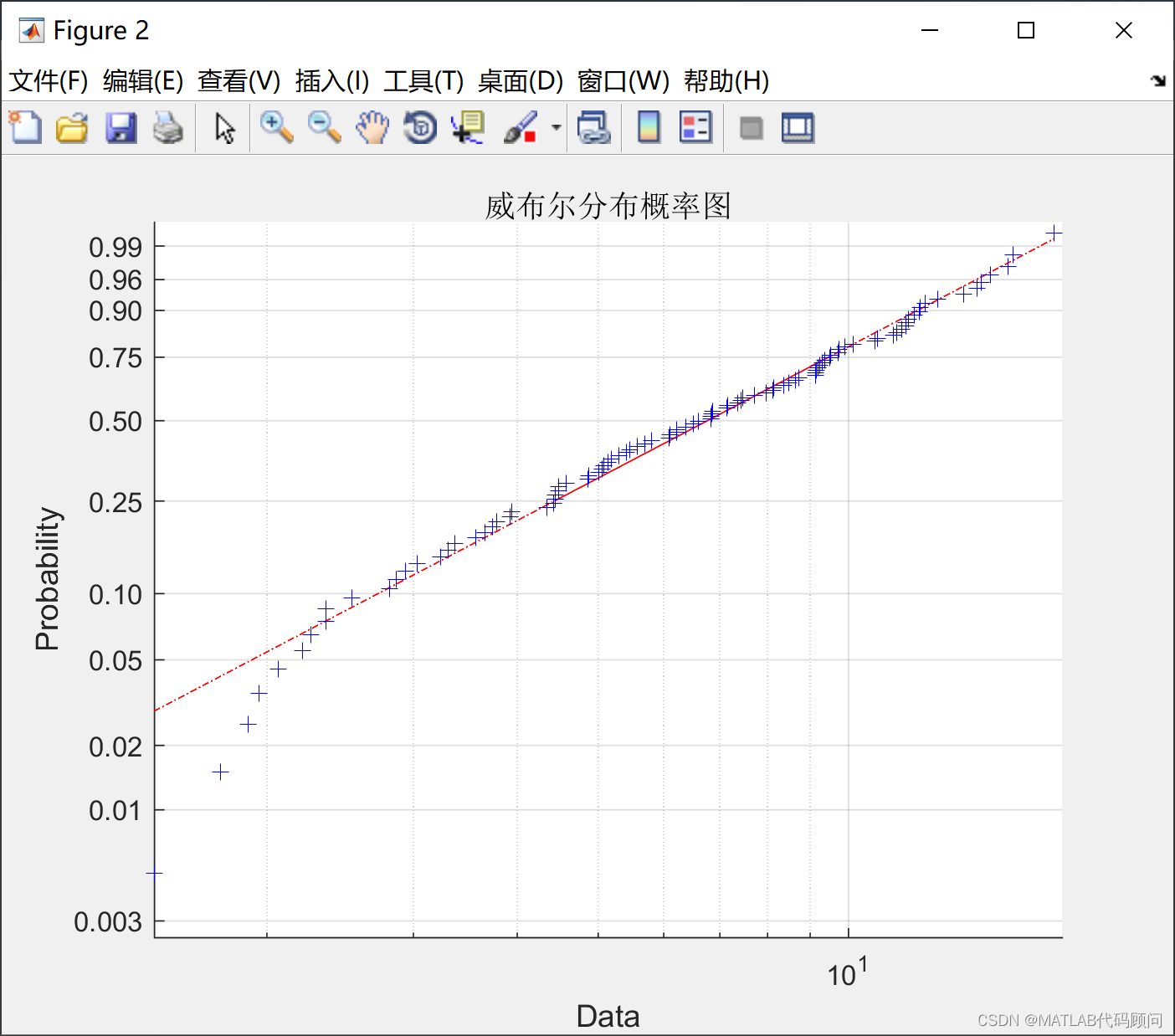
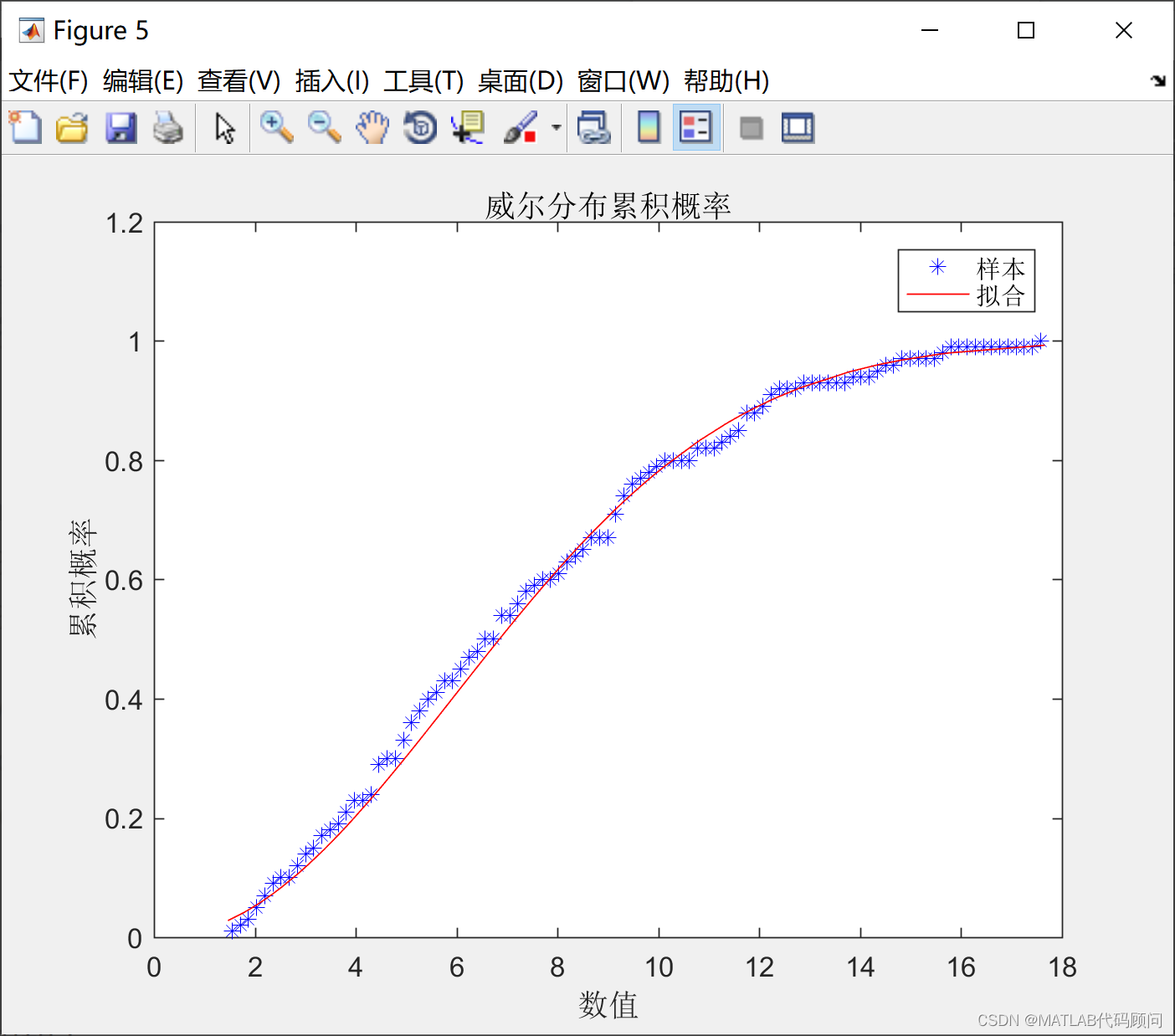







 文章介绍了如何使用最大似然估计方法来拟合威布尔分布,通过样本数据计算对数似然函数并求导,得出位置参数λ的估计值,即样本数据的平均值。给出了一个实际例子,展示了如何用Matlab编程实现这一过程。
文章介绍了如何使用最大似然估计方法来拟合威布尔分布,通过样本数据计算对数似然函数并求导,得出位置参数λ的估计值,即样本数据的平均值。给出了一个实际例子,展示了如何用Matlab编程实现这一过程。


















 1146
1146

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










