线性代数及其应用 1.1线性方程组

哈喽，大家好。这里是37的数学屋。第一次发表个人的学习思路，有不足的地方还希望各位谅解(不然又要被6敲打了)

这节我们浅谈一下线性方程组。我们知道，线性代数和线性方程组都有两个字————“线性”，可见线性方程组在线性代数当中的地位有多高。咱们这一节和下一节，也就是1.2主要介绍一下线性方程组的一个常规方法。好了，话不多说，我们进入正题。

我们先简单介绍一下什么是线性方程：

        线性方程是形如

        并且包含变量的方程。其中b和系数可以是实数或者是复数，通常是已知数，下标n可以是任意大的正整数。看到这里，相信大家都猜到了什么是线性方程组，其实就是这些线性方程组合在一起就叫线性方程组啦。

那么，这里又涉及到了另一个概念(严肃)，线性方程，线性线性，啥是线性？

其实，线性可以简单概括为：一次。

如果两个变量之间存在一次方函数关系，就称它们之间存在线性关系。在二维的平面内，这类线性方程的图像实际上为一条直线。

那么线性方程组比较正式一点的定义是：由一个或者几个包含相同变量的线性方程组成的。

例如：

而方程组的解则是一组数,意思就是说，当我们用这些数来分别代替方程组中对应的x时，会得到一个恒等式。我们把这样的若干个解划分在一个集合里，把这个集合称之为解集。

如果两个方程组的解集一样(集合的性质)，我们就称这两个方程组是等价的。

看到这里，相信许多小伙伴都猜到了，我们要求线性方程组的解，实际上就是去求这两个线性方程在平面坐标上的交点。

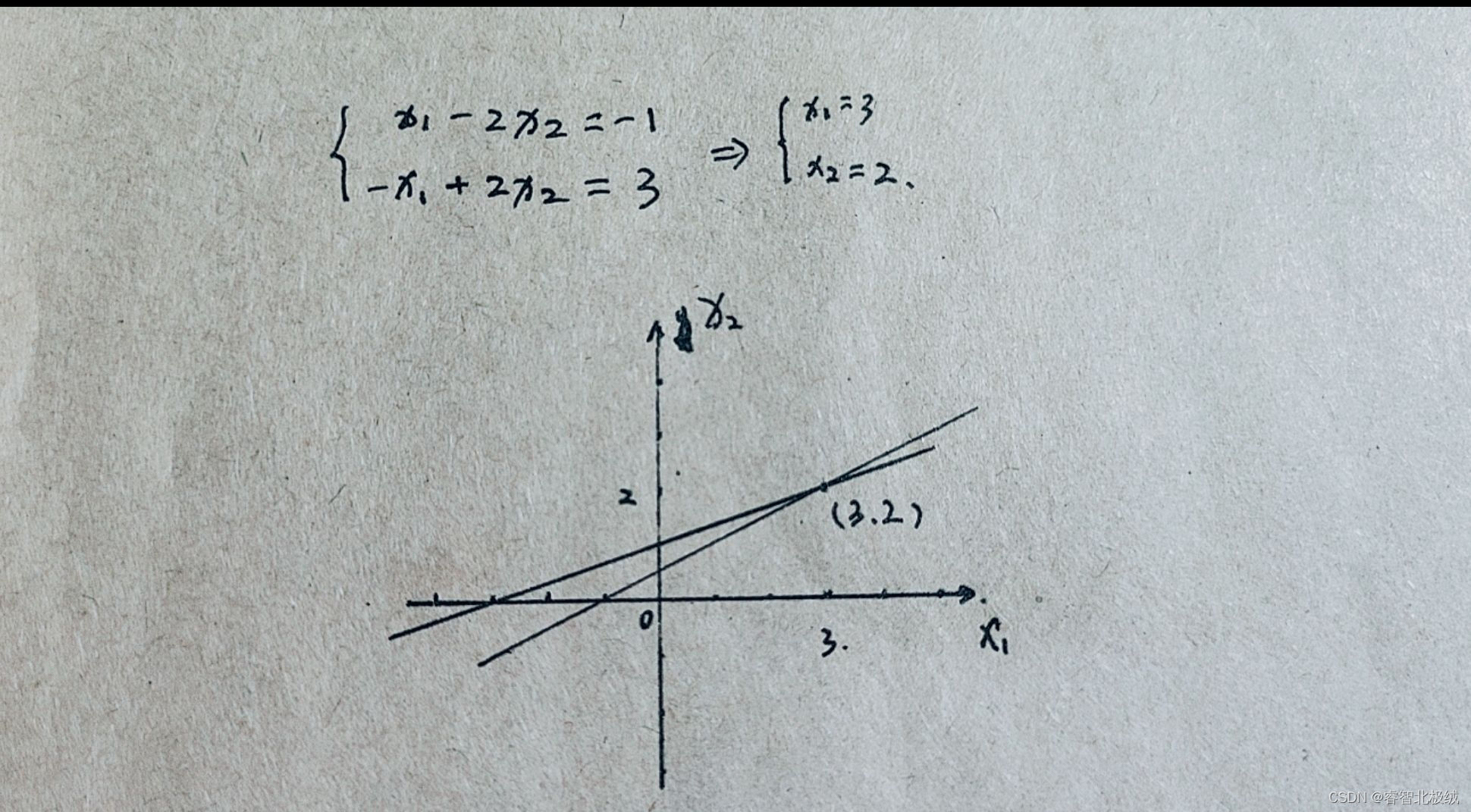
既然是求交点，那肯定会涉及到有无解，有无无数解的情况。

             

所以，线性方程组的解有下列三种情况：

1. 无解
2. 有唯一解
3. 有无穷多个解

(证明会在下一节讲解)

这里又涉及到一个基本概念：相容性

如果它有一个解或者有无穷多个解，我们就称这个线性方程组是相容的；如果它无解，则称它是不相容的。

好了，我们现在已经了解了基本的线性方程组概念，就可以试着去解一些线性方程组了。不过在实际操作之前，我们还要学会一种常见写法——矩阵记号

一个线性方程组包含的主要信息我们可以把它们用一个紧凑的矩形阵列表示，这个矩形矩阵就称之为矩阵。

这个写法很重要，我们之后解线性方程组都要用到它。实际上也不难，就是把每一个x前的系数提取出来，写在对齐的一列中。

                                                  

                                                                     

                          

 

得到的矩阵为       

这种只有x系数的矩阵我们称之为系数矩阵。

而有这么一类矩阵，连方程组的等式右边也写了进去，我们就称这类矩阵为增广矩阵。

      

通俗来讲，增广矩阵就是在系数矩阵上添加一列所得，这一列就是方程组右边的常数组陈。

我们知道，矩阵包含了行和列，比如上面的增广矩阵就是一个3行4列的矩阵.那么矩阵的维数就说明了它包含的行数和列数。

这里有一个直观的概括：若m,n是正整数，m*n矩阵就是一个m行n列的数的矩形阵列。

简单记为：行在前，列在后

========================================================================= 小节分割线

=========================================================================

欧克，我们现在已经学会了解方程组的基本写法，下面来学习一下解方程组的思路。

我们线性方程组的思路一般是用一个更容易解的等价方程组来替代原来的方程组，粗略的概括就是我们用方程组中含有的项去消去其他方程中含有的项，用第二个方程中含的项消去其他方程中含有的项，以此类推就会得到一个简化的方程组。

我们这里引入化简线性方程组的三个基本范式：

1. 两个方程组相加
2. 两个方程组的位置交换

把某一个方程等式两边同时乘以一个非0常数

例如：

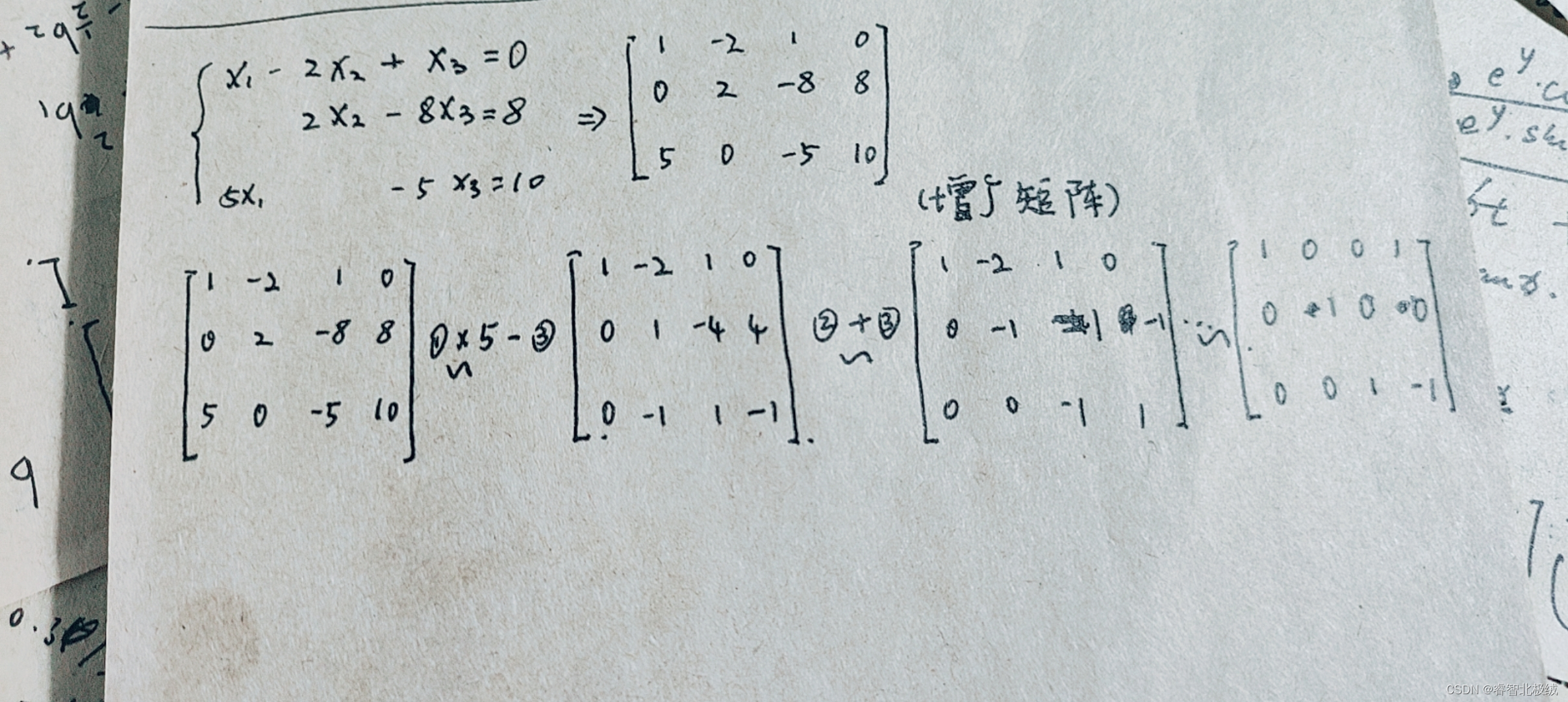
这个例子说明了线性方程的变换和增广矩阵的行变换对应。

补充一点，增广矩阵的行变换也是三种：

1. 倍加变换    把某一行换成它本身与另一行的倍数
2. 对换变换    把两行位置对换
3. 倍乘变换    把莫一行的所有元素乘以同一个非零数

其实行变换不仅仅是可以施行于增广矩阵，对于任何矩阵都是适用的。如果现在有两个矩阵摆在你的面前，其中一个矩阵可以经过一系列行变换成为另一个矩阵，我们就称这两个矩阵是行等价的

那么，有些细心的朋友可能会意识到，我们可以将某一方程两边同时乘以常数c，那也可以将变换后的方程两边同时除以常数c得到原方程，同理，面对两个倍加变换的方程，把其中一个方程的c倍减去也会得到原来的方程，这个有趣的性质就是行变换的可逆性

由于新的方程组是由原方程组经过各类行变换得到的，所以我们大胆猜测这两个方程组的解集是不是相同的呢？

当然，我都这么说了，那肯定是相等的啦。

所以就有了这样的一个推论：

若两个线性方程组的增广矩阵是行等价的，那么它们就具有相同的解集

尽管解方程组的方法比较麻烦，但我们仍然在熟练后可以很快地看出，毕竟没有人会把特别复杂的数类运算塞到一个矩阵里。方法，方法最重要。

好啦，这节的分享就到这里啦，觉得还可以的话给点个关注吧