【初等数论】阶断性总结(未完结)

导言

数论是信息竞赛$($当然数竞也要学$)$中一重大分支，其主要研究整数环的整除理论及同余理论，此外它也包括了连分数理论和少许不定方程的问题。本质上说，初等数论的研究手段局限在整除性质上

大纲

• 整除
• 模运算
• 同余
• 排列组合
• 质数筛
• 最大公约数与最小公倍数
• 裴蜀定理
• 拓展欧几里得
• 费马小定理
• 逆元

一.整除

定义：

设$a,b\in \mathbb{Z}$，$a\ne 0$，如果$\exists$一个数$q\in \mathbb{Z}$，使得$a\cdot q=b$， 则$b$能被$a$整除， 记作$a\mid b$, 否则$a\nmid b$

性质

①：
如果$a\mid b$，且$b\mid c$，则 $a\mid c$
证明：

$\because$ $a\mid b$
$\therefore a\cdot x=b(x\in \mathbb{Z}$ 且 $x\ne 0)$
$\because$ $a\mid c$
$\therefore b\cdot y=c(y\in \mathbb{Z}$ 且 $y\ne 0)$
$\because$ $a\cdot x\cdot y=c$
$\therefore a\mid c$

②：
若 $a\mid b$ 且 $a\mid c$，则 $a\mid (b\cdot x+c\cdot y)$
证明：

设$b=a\cdot q$，$c=a\cdot p$
那么 $b\cdot x+c\cdot y=a\cdot q\cdot x+a\cdot q\cdot y=a(q\cdot x+p\cdot y)$
$\because$ $a\mid a\cdot (q\cdot x+p\cdot y)$
$\therefore a\mid (b\cdot x+c\cdot y)$

③：
设 $m\ne 0$，则 $a\mid b$ 等价于 $a\cdot m\mid b\cdot m$
证明：

令 $b=a\cdot x(x\in \mathbb{Z})$
$\because$ $a\cdot m\mid a\cdot m\cdot x$
$\therefore a\cdot m\mid b\cdot m$

④：
设整数 $x,y$ 满足下式：$a\cdot x+b\cdot y=1,$ 且 $a\mid n$，$b\mid n$，那么 $a\cdot b\mid n$
证明：

证明 $a\cdot b\mid n$ 即证明 $\frac{n}{a\cdot b}\in \mathbb{Z}$
设 $a=\frac{n}{k_1}(k1\in \mathbb{Z}),b=\frac{n}{k_2}(k2\in \mathbb{Z})$
那么 $\frac{n}{a\cdot b}=\frac{n}{\frac{n^2}{k1\cdot k2}}=\frac{k1\cdot k2}{n}$
$\because$ $a\cdot x+b\cdot y=1$
$\therefore$ $\frac{n\cdot x}{k_1}+\frac{n\cdot y}{k_2}=1$
$\therefore$ $n\cdot x+n\cdot y=k1\cdot k2$
$\therefore$ $n\cdot (x+y)=k1\cdot k2$
$\therefore$ $\frac{k1\cdot k2}{n}=x+y$
$\because x,y\in \mathbb{Z}$
$\therefore \frac{k1\cdot k2}{n}\in \mathbb{Z}$
$\because$ $\frac{n}{a\cdot b}$ $=$ $\frac{k1\cdot k2}{n}$

$\therefore \frac{n}{a\cdot b}\in \mathbb{Z}$
$\therefore a\cdot b\mid n$

⑤：若 $b=q\cdot d+c$，那么 $d\mid b$ 的充要条件是 $d\mid c$
备注：充要条件 即充分必要条件，意思是说，如果能从命题$p$推出命题$q$，而且也能从命题$q$推出命题$p$ ，则称$p$是$q$的充分必要条件，且$q$也是$p$的充分必要条件
$(1)$

若 $d\mid b$, 则 $b$ 可以表示为$p\cdot d(p\in \mathbb{Z})$
$\therefore p\cdot d=q\cdot d+c$
$\therefore (p-q)\cdot d=c$
$\because (p-q)\in \mathbb{Z}$
$\therefore d\mid c$

$(2)$

$d\mid c$, 则 $c$ 可以表示为$p\cdot d(p\in \mathbb{Z})$
则 $b=q\cdot d+p\cdot d=(q+p)\cdot d$
$\therefore d\mid b$

二.模运算

定义：

对于整数 $a,b$，其中$b\ne 0$，求$a$整除$b$的余数，称为$a$模$b$，记为$a$ $mod$ $b$

①分配率

1 ) $(a+b)$ $mod$ $c=(a$ $mod$ $c+b$ $mod$ $c)$ $mod$ $c$
证明：

设 $a=k_1\cdot c+r_1(k_1\in \mathbb{Z})$，$b=k_2\cdot c+r_2(k_2\in \mathbb{Z})$
$(a+b)$ $mod$ $c$
$=[(k1+k2)\cdot c+r1+r2]$ $mod$ $c$
$=(r1+r2)$ $mod$
$(a$ $mod$ $c+b$ $mod$ $c)$ $mod$ $c$
$=(r1+r2)$ $mod$ $c$
$\therefore $ $(a+b)$ $mod$ $c=(a$ $mod$ $c+b$ $mod$ $c)$ $mod$ $c$

2 ) $(a-b)$ $mod$ $c=(a$ $mod$ $c-b$ $mod$ $c)$ $mod$ $c$

与加法分配率类似，故不予证明

3 ) $(a\cdot b)$ $mod$ $c=(a$ $mod$ $c\cdot b$ $mod$ $c)$ $mod$ $c$

与加法分配率类似，故不予证明

4 ) $(a^b)$ $mod$ $c=(a$ $mod$ $c$)${}^b$ $mod$ $c$

与加法分配率类似，故不予证明

②放缩性

1 ) $a$ $mod$ $b=c$，则$a\cdot d$ $mod$ $b\cdot d=c\cdot d$

证明：不妨设$a=k\cdot b+c(k\in \mathbb{Z})$
则 $(a\cdot b)$ $mod$ $(b\cdot d)=(k\cdot b\cdot d+c\cdot d)$ $mod$ $(b\cdot d)=c\cdot d$ $mod$ $b\cdot d$
$\because$ $a$ $mod$ $b=c$
$\therefore c<b$
$\therefore c\cdot d<b\cdot d$
$\therefore$ $c\cdot d$ $mod$ $b\cdot d=c\cdot d$
$\therefore$ $a\cdot d$ $mod$ $b\cdot d=c\cdot d$

2 ) $a$ $mod$ $b=c$，$d\mid a$ 且 $d\mid b$ , $a÷d$ $mod$ $b÷d=c÷d$

证明：不妨设 $a=k_1\cdot d,b=k_2\cdot d$
$a$ $mod$ $b=k_1\cdot d$ $mod$ $k_2\cdot d=$ $d\cdot ($ $k_1$ $mod$ $k_2)$
$a÷d$ $mod$ $b÷d=k1$ $mod$ $k2=c$

三.同余

概念：

设$m$是给定的正整数，若满足$m\mid (a-b)$，则称$a$与$b$对模$m$同余，记作$a\equiv b(\mathrm{mod}m)$，若$m\nmid (a-b)$，则$a$与$b$对模$m$不同余

性质

① 自反性：$a\equiv a(\mathrm{mod}m)$

显然，故不予证明

② 对称性：若 $a\equiv b(\mathrm{mod}m)$，那么$b\equiv a(\mathrm{mod}m)$
证明：

$\because a\equiv b(\mathrm{mod}m)$
$\therefore$ $a$ $mod$ $m=b$ $mod$ $m$
$\therefore b\equiv a(\mathrm{mod}m)$

③ 传递性：若 $a\equiv b(\mathrm{mod}m)$ 且 $b\equiv c(\mathrm{mod}m)$，那么 $a\equiv c(\mathrm{mod}m)$
证明：

$\because a\equiv b(\mathrm{mod}m)$
$\therefore$ $a$ $mod$ $m=b$ $mod$ $m$
又$\because b\equiv c(\mathrm{mod}m)$
$\therefore$ $c$ $mod$ $m=b$ $mod$ $m$
$\therefore$ $a$ $mod$ $m=c$ $mod$ $m$
$\therefore a\equiv c(\mathrm{mod}m)$

④ 同加性：若 $a\equiv b(\mathrm{mod}m)$，那么$a+c\equiv b+c(\mathrm{mod}m)$
证明：

$\because a\equiv b(\mathrm{mod}m)$
$\therefore$ $a$ $mod$ $m=b$ $mod$ $m$
$\because a+c$ $mod$ $m=a$ $mod$ $m+c$ $mod$ $m$
又$\because b+c$ $mod$ $m=b$ $mod$ $m+c$ $mod$ $m$
$\therefore$ $a+c$ $mod$ $m=b+c$ $mod$ $m$
$\therefore$ $a+c\equiv b+c(\mathrm{mod}m)$

⑤ 同减性：若 $a\equiv b(\mathrm{mod}m)$，那么$a-c\equiv b-c(\mathrm{mod}m)$

与同加性证明类似，故不予证明

⑦ 同减性：若 $a\equiv b(\mathrm{mod}m)$，那么$a-c\equiv b-c(\mathrm{mod}m)$

与同加性证明类似，故不予证明

⑥ 同乘性：若 $a\equiv b(\mathrm{mod}m)$，那么$a\cdot c\equiv b\cdot c(\mathrm{mod}m)$

与同加性证明类似，故不予证明

⑧ 同除性：若 $a\equiv b(\mathrm{mod}m)$，且$c\mid a$， $c\mid b$，$(a,b)=1$，那么$ \dfrac{a}{c} \equiv \dfrac{b}{c} \pmod m$
证明：

不妨设 $a=k1\cdot m+r,b=k2\cdot m+r$
$ \dfrac{a-b}{c}= \dfrac{(k1-k2) \cdot m}{c}$
$ \because c \mid a$ 且 $c\mid b$
$ \therefore \dfrac{a-b}{c} \in \mathbb{Z}$
$ \therefore \dfrac{(k1-k2) \cdot m}{c} \in \mathbb{Z}$
$ \because (a,b)=1$
$ \therefore c \mid (k1-k2)$
$ \therefore m \mid \dfrac{(k1-k2) \cdot m}{c}$
$ \therefore m \mid \dfrac{a-b}{c})$
$ \therefore \dfrac{a}{c} \equiv \dfrac{b}{c} \pmod m$

⑨ 同幂性：若 $a\equiv b(\mathrm{mod}m)$，那么$a^c\equiv b^c(\mathrm{mod}m)$
证明：

$\because a^c=(a$ $mod$ $m{)}^c$
又 $\because b^c=(b$ $mod$ $m{)}^c$
$\therefore a^c=b^c$
$\therefore a^c\equiv b^c(\mathrm{mod}m)$

⑩ 互加性：若 $a\equiv b(\mathrm{mod}m)$，$c\equiv d(\mathrm{mod}m)$，那么$a+c\equiv b+d(\mathrm{mod}m)$
证明：

不妨设
$a=k_1\cdot m+r_1$
$b=k_2\cdot m+r_1$
$c=k_3\cdot m+r_2$
$d=k_4\cdot m+r_2$
那么 $(a+c)$ $mod$ $m=(r1+r2)$ $mod$ $m$
$(b+d)$ $mod$ $m=(r1+r2)$ $mod$ $m$
$\therefore a+c\equiv b+d(\mathrm{mod}m)$

? 互乘性：若 $a\equiv b(\mathrm{mod}m)$，$c\equiv d(\mathrm{mod}m)$，那么$a\cdot c\equiv b\cdot d(\mathrm{mod}m)$
证明：

$a\cdot c$ $mod$ $m=a$ $mod$ $m\cdot c$ $mod$ $m$
$b\cdot d$ $mod$ $m=b$ $mod$ $m\cdot d$ $mod$ $m$
$\because a$ $mod$ $m=b$ $mod$ $m$
又$\because c$ $mod$ $m=d$ $mod$ $m$
$\therefore a\cdot c\equiv b\cdot d(\mathrm{mod}m)$

推论

①：若2能整除a末位，则$2\mid a$
证明：

设 $a$ 为 $ \overline {k_1k_2k_3k_4k_5 \cdots k_n}$
$a$ $mod$ $2=(\overline{k_1{k}_2{k}_3{k}_4{k}_5\cdots k_{n-1}}\times 10+k_n)$ $mod$ $2=k_n$ $mod$ $2$

②：若4能整除a末两位，则 $4\mid a$
证明：

设 $a$ 为 $ \overline {k_1k_2k_3k_4k_5 \cdots k_n}$
$a$ $mod$ $4=(\overline{k_1{k}_2{k}_3{k}_4{k}_5\cdots k_{n-2}}\times 100+k_n)$ $mod$ $4=\overline{k_{n-1}{k}_n}$ $mod$ $4$

③：推广，若$2^n$能整除a的末$n$位，则$2^n\mid a$

证法同①②，故不予证明

④：若$3$能整除$a$的各个位之和，则 $3\mid a$
证明：

设 $a$ 为 $ \overline {k_1k_2k_3k_4}$
$a$ $mod$ $3=(k_1\cdot (999+1)+k_2\cdot (99+1)+k_3\cdot (9+1)+k_4)$ $mod$ $3=(k_1+k_2+k_3+k_4)$ $mod$ $3$

⑤：若$9$能整除$a$的各个位之和，则 $9\mid a$

证法同④，故不予证明

⑥：若$11$能整除$a$的偶数位之和与奇数位之和的差，则 $11\mid a$
证明：

设 $a$ 为 $ \overline {k_1k_2k_3k_4k_5k_6k_7}$
$a$ $mod$ $11=(k_1\cdot (999999+1)+k_2\cdot (100001-1)+k_3\cdot (9999+1)+k_4\cdot (1001-1)+k_5\cdot (99+1)+k_6\cdot (11-1)+k_7))$ $mod$ $11=(k_1+k_2+k_3+k_4)$ $mod$ $11$

⑦：若能被$7$，$11$，$13$整除的数的特征是，这个数末三位与末三位以前所分别组成的数字的差能被$7$，$11$，$13$整除
证明：

结论转化：能被$7$，$11$，$13$整除的数即是能被$1001$整除的数
设 $a$ 为 $ \overline {k_1k_2k_3k_4k_5k_6k_7}$
$a$ $mod$ $1001=(\overline{k_1{k}_2{k}_3{k}_4}\cdot (1001-1)+\overline{k_1{k}_2{k}_3})$ $mod$ $1001=(\overline{k_1{k}_2{k}_3}-\overline{k_1{k}_2{k}_3{k}_4})$ $mod$ $1001$

四.排列组合

定义：

• 排列：给定的元素中，取出指定个数的元素，进行排序，记为$A(Arrangement)$
• 组合: 给定的元素中，取出指定个数的元素，不考虑排序，记为$C(Combination)$

计算方法

• 排列：情景创造，设从$n$个小球中取出$m$个放入指定篮子里，则第一个篮子有$n$种选择，第二个篮子有$n-1$种选择，以此类推，直至最后一个篮子有$n-m+1$种选择，根据乘法原理，故 $A_m^n={\prod }_{i=m-n+1}^{n}i$，即 $\frac{n!}{(n-m)!}$

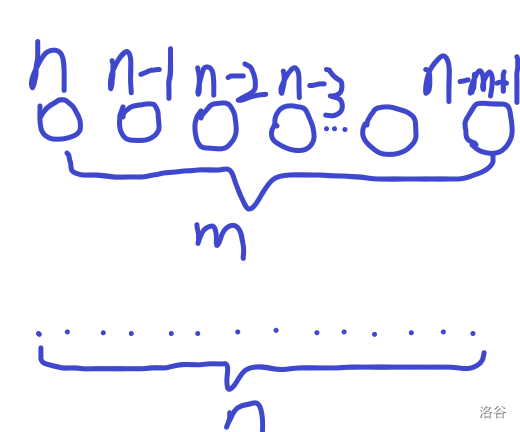
• 组合：因为不考虑排序，所以排列即是在每个合法组合中交换两数位置，最终每个组合会多$m!$种可能，所以$C_m^n=A_m^n÷m!=\frac{n!}{(n-m)!\cdot m!}$

盒子与球模型

①球相同，盒不同，无空盒
推导：

设有$n$个小球和$m$个盒子
运用隔板法，要满足$m$个盒子无空盒，则需要$(m-1)$个隔板，而每两个小球之间有一个缝隙，故有$(n-1)$个可安插隔板的位置,因为球相同，故使用组合数，最后答案为 $C_{n-1}^{m-1}$

如下图，红色代表安插隔板的位置

②球相同，盒不同，有空盒
推导：

$\because$ 允许空盒
$\therefore$ 我们先在每个盒子里放上一个虚拟的球，后按无空盒问题处理即可，最后答案为 $C_{n+m-1}^{m-1}$

③球不同，盒相同，无空盒
推导：

定义$dp[i][j]$有$i$个小球和$j$个盒子的情况
因为不允许有空盒，所以对于第$i$个盒子来说，只需考虑两种情况：该小球独占一个盒子和与其他小球用这$j$个盒子，因为球不同，所以对于第二种情况来说，有$j$种可能，而对于第一种情况来说，因为盒相同，所以有且只有一种可能
故状态转移方程应为 $d{p}_{i,j}=d{p}_{i-1,j-1}+d{p}_{i-1,j}$

④球不同，盒相同，有空盒
推导：

因为与③的差异只在于允许空盒，那么我们只需要在③的基础上枚举有多少个空盒，然后把其累加即可
故答案为 ${\sum }_{i=1}^{m}d{p}_{n,i}$

⑤球不同，盒不同，无空盒
推导：

该模型与与③类似，因为盒不同，所以对于③的每个合法组合都多了$m!$种可能
故答案为 $d{p}_{n,m}\cdot m!$

⑥球不同，盒不同，有空盒
推导：

对于每个小球来说都有$m$种放法
故答案为 $m^n$

⑦球相同，盒相同，无空盒
推导：

状态仍旧为 $d{p}_{i,j}$
对于 $d{p}_{i,k}$，因为不允许有空盒，所以我们先借$j$个小球放入$j$个盒子里，然后再由$ dp_{i-j,k}(1 \leq k \leq j)$转移过来
故状态转移方程为 $d{p}_{i,j}={\sum }_{k=1}^{j}d{p}_{i-j,k}$
答案为 ${\sum }_{i=1}^{m}d{p}_{n-m,i}$

⑧球相同，盒相同，有空盒
推导：

与②到③的思路无异，先把每个盒子里放入一个虚拟的球，然后按⑦解决即可
故答案为 $dp[n+m][m]$

五.质数筛

相关概念

• 质数：大于$1$的自然数中除了$1$和该数自身外，无法被其他自然数整除的数
• 筛法：顾名思义，就是把一些特定的数筛出去。这里的质数筛法一般指的是把一些数的倍数筛掉。筛到第$n$个数了，比$n$小的数就都是质数了

① 暴力筛法

即把$(1,n]$中所有的倍数筛去，留下的即为质数
时间复杂度：$O(n$ $\ln$ $n)$
核心代码：

for (int i = 2 ; i * i <= n ; i ++) {
	for (int j = i ; j * i <= n ; j ++) {
		vis[i * j] = 1;
	}
}

② 埃拉托斯特尼筛法(埃筛)

一个数如果有因子，那它一定有质因子，所以我们只需把质数的倍数筛去即可
时间复杂度：$O(n$ $\ln$ $n)$
核心代码：

for (int i = 2 ; i * i <= n ; i ++) {
	if (vis[i]) continue;
	for (int j = i ; j * i <= n ; j ++) {
		vis[i * j] = 1;
	}
}

③ 欧拉筛(线性筛)

埃筛重复计算的原因：一个数被它的多个质因子筛了多次，造成了耗时的增长
解决方案：确保一个数只被它的最小质因子筛掉，这就是欧拉筛的原理

• 建立一个数组$prime$用来保存已知的质数
• 枚举$i(1\le i\le n)$，把$i$作为倍数，并把$prim{e}_j(1\le j\le len)$与$i$的乘积筛去
• 若当前$prim{e}_j$为$i$的倍数，则$break$，因为$i$的倍数一定会被$prim{e}_j$筛掉
• $prime$里存储的则是$1-n$的质数

时间复杂度：$O(n)$
核心代码：

for (int i = 2 ; i <= n ; i ++) {
	if (!vis[i]) a[++ cnt] = i;
	for (int j = 1 ; j <= cnt && a[j] * i <= n ; j ++) {
		vis[i * a[j]] = 1;
		if (i % a[j] == 0) break;
	}
}

六.最大公约数与最小公倍数

定义

• $gcd$： 一般设$a_1,a_2,a_3\cdots a_k$是$k$个${\mathbb{Z}}^{+}$，如果存在一个正整数$d$，使得$d\mid a_1,d\mid a_2,d\mid a_k$，那么$d$则为$a_1{a}_2\cdots a_k$的公约数
• $lcm$： 一般设$a_1,a_2,a_3\cdots a_k$是$k$个${\mathbb{Z}}^{+}$，如果存在一个正整数$d$，使得$a_1\mid d,a_2\mid d,a_k\mid d$，那么$d$则为$a_1{a}_2\cdots a_k$的公倍数

定理

① $lcm(a,b)\cdot gcd(a,b)=a\cdot b$
证明：

将$a,b$进行质因子分解
设$a,b$质因子集合并为 { P 1 , P 2 ⋯   , p n } \{ P_1,P_2 \cdots,p_n \} {P1​,P2​⋯,pn​}
那么，可设 $a={\prod }_{i=1}^n{P}_i^{k_i}$，$b={\prod }_{i=1}^n{P}_i^{j_i}$
$gcd(a,b)={\prod }_{i=1}^n{P}_i^{min(k_i,j_i)}$
$lcm(a,b)={\prod }_{i=1}^n{P}_i^{max(k_i,j_i)}$
又 $\because min(k_i,j_i)+max(k_i,j_i)=k_i+j_i$
$\therefore gcd(a,b)\cdot lcm(a,b)={\prod }_{i=1}^n{P}_i^{k_i+j_i}=a\cdot b$

② 辗转相除法：$gcd(a,b)=gcd(b,a$ $mod$ $b)$
证明：

设 $a=kb+r(k,r\in \mathbb{Z}),d=gcd(a,b)$
$\because r=a-kb$
$\therefore \frac{r}{d}=\frac{a}{d}-\frac{kb}{d}$
$\because \frac{a}{d},\frac{kb}{d}\in \mathbb{Z}$
$\therefore d\mid r$
$\because d$为$b$的最大因子且为$a$ $mod$ $b$的因子
$\therefore gcd(b,a$ $mod$ $b)=d$

七.裴蜀定理

公式

对于不定方程$ax+by=m$，其有解的充要条件是 $gcd(a,b)\mid m$

• 对于充分性，后在扩展欧几里得提及
• 对于必要性
  证明：

$\because ax+by=m$
$\therefore$ 有整数$x,y$使得$ax+by=m$
又$\because gcd(a,b)\mid a$
$\because gcd(a,b)\mid b$
$\therefore gcd(a,b)\mid (a\cdot x+b\cdot y)$
$\therefore gcd(a,b)\mid m$

引理

① 对于$\forall x,y\in \mathbb{Z}$，函数$f(x,y)=a\cdot x+b\cdot y$的最小正整数取值为$gcd(a,b)$
证明：

设集合 A = { m ( a ⋅ x + b ⋅ y = m ) , x , y ∈ Z A=\{m(a \cdot x+b \cdot y=m),x,y \in \mathbb{Z} A={m(a⋅x+b⋅y=m),x,y∈Z
结论转化：设$S$为$A$中最小的元素，证明$gcd(a,b)=s$ 就等价于证明 $gcd(a,b)\mid s$ 且 $s\mid gcd(a,b)$
$\because S$为$A$集中最小元素
$ \therefore $满足线性方程 $a\cdot x_0+b\cdot y_0=S$
又 $\because gcd(a,b)\mid a$
$\therefore gcd(a,b)\mid a\cdot x_0$
同理 $gcd(a,b)\mid b\cdot y_0$
$\therefore gcd(a,b)\mid S$
设$a=q\cdot s+r(0\le r<s)$
$r$
$=a-q\cdot s$
$=a-q\cdot (a\cdot x_0+b\cdot y_0)$
$=a\cdot (1-q\cdot x_0)+b\cdot (-q\cdot y_0)$
$\because a\cdot (1-q\cdot x_0)+b\cdot (-q\cdot y_0)$与$a\cdot x_0+b\cdot y_0$是一致的线性方程
$\therefore r\in A$
又$\because S$为$A$中最小的正整数，且$(0\le r<s)$
$\therefore S=0$
$\therefore S\mid a$
$\therefore S\mid b$
$\therefore S\mid gcd(a,b)$

② 如果$a,b$为正整数，且$(a,b)=1$，则不存在小于$b$的正整数