Fast Gradient Sign Method (FGSM)原理细节及代码实现

基于梯度的攻击方法有很多，其基本思路主要是两个：

• 对约束标准做改动，如$L2-norm$、$L-infinity$等。
• 对优化方案做改动
  

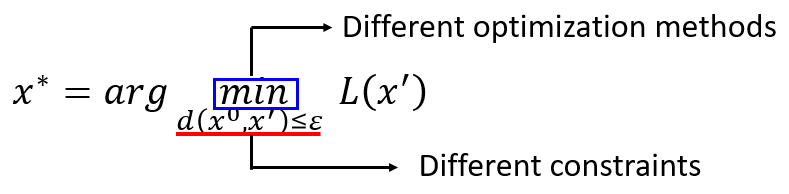
可以说FGSM是最简单的攻击方法。它的思路很简单：网络参数$\theta$保持不变，损失函数$L$对原始输入$x^0$的所有维度求导，若值为正数，取1；值为负数，取-1。得到$\Delta$$x$。
实际上，如果$\Delta$$x$中没有符号函数$sign$参与计算，那么得到的就是梯度方向。而加上$sign$之后，得到的$\Delta$$x$就不是准确的梯度方向了，就成了作者做说的“梯度符号”。
不过我们依然可以把它理解成梯度方向，这样原始样本$x^0$往梯度的反方向前进$\epsilon$距离。$\epsilon$是扰动约束，可以理解为一个很大的学习率。这样整个过程就是按照梯度下降的方法优化一次，而且一步到位。

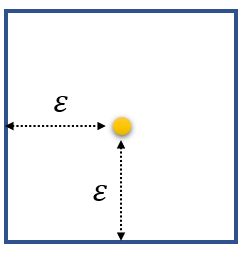
假设扰动约束$\epsilon$使用$L-infinity$。那么扰动空间就成了一个方形，原始样本距离每条边的距离都是$\epsilon$。如下图所示。

首先算出原始样本$x^0$的梯度，如下图：

正常的梯度下降方式为：原始参数$x^0$+（梯度的反方向*学习率），得到的结果为下图中的$x^1$。

而FGSM是一部到位，直接得到右上角的$x^{\ast }$。

它关注的不是$gradient$的具体方向，不管$gradient$指向左下角的哪一个方向，$x^{\ast }$始终会落到右上角。因为向量$\Delta$$x$是方向指向左下角正方向且每个维度的绝对值都为1的向量。如下图红色箭头所示。

同理，如果$gradient$在左上角的任何一个方向，对抗样本$x^{\ast }$始终会落在右下角那个点。

实际上，FGSM是对样本$x^0$进行一次梯度下降的过程，该过程的学习率足够大，以至于可以一步到位。超出的部分由约束$\epsilon$进行截断（每个维度的最大值是$\epsilon$）。