【长文阅读】MAMBA作者博士论文＜MODELING SEQUENCES WITH STRUCTURED STATE SPACES＞-Chapter5 HIPPO as Orthogonal SSMs

Chapter 5 HIPPO as Orthogonal SSMs

Gu A. Modeling Sequences with Structured State Spaces[D]. Stanford University, 2023.

本文是MAMBA作者的博士毕业论文，为了理清楚MAMBA专门花时间拜读这篇长达330页的博士论文，由于知识水平有限，只能尽自己所能概述记录，并适当补充一些相关数学背景，欢迎探讨与批评指正。内容多，分章节更新以免凌乱

第五章通过SSM的视角重新审视了HIPPO框架，将其细化并推广到了一系列新的状态空间模型。这一部分包括对HIPPO的多种实例化，以及如何初始化这一系列SSM的各个参数。

5.1 Framework: Revisiting HIPPO as Orthogonal SSMs

本节从 SSM 的角度重新审视 HIPPO 框架，并引入正交 SSM 的概念，捕捉其在线记忆的主要目的。

5.1.1 Summary of HIPPO Matrices

本节先回顾了之前章节HIPPO 生产的多种具有特定公式的算子：

明确第一步是用 SSM 语言重新表述 HIPPO 算子的定义。 HIPPO 的目标是找到一个适当选择的 SSM 基 $(A,B)$，以便在任何时间 $t$，当前状态 $x(t)$ 可以用于近似重建直到时间 $t$ 的整个输入 $u$。

5.1.2 Orthogonal State Space Models

论文首先给出了一些抽象定义：

定义5.1 如果一个状态空间模型（SSM）由$(A(t),B(t))$组成，并且对于基函数$p_n(t,s)$和非负的测量函数$\omega (t,s)\ge 0$，SSM基内核$K_n(t,s)=p_n(t,s)\omega (t,s)$在所有时间点$t$满足以下条件，那么这个SSM称为正交状态空间模型（O-SSM）：

在所有时间点t，$x_n(t)={\int }_{-\infty }^t{K}_n(t,s)u(s)ds$ (5.4)

并且 ${\int }_{-\infty }^t{p}_n(t,s)p_m(t,s)\omega (t,s)ds={\delta }_{nm}$

其中，${\delta }_{nm}$是Kronecker delta函数。

对于时不变 O-SSM (TO-SSM) ，$K_n(t,s)=:K_n(t-s)$,给定$\omega (t-s):=\omega (t,s)$和$p_n(t-s):=p_n(t,s)$

对于 O-SSM，$(p,\omega )$ 和 $K$ 是彼此唯一确定的，因此我们可以通过其中之一来引用 OSSM。一个方向是显而易见的：$(p,\omega )$通过 $K_n(t,s)=p_n(t,s)\omega (t,s)$ 确定 $K$。

这个公式第一次看符号较多，论文说明较少，对这个定义补充解读一下：

定义5.1中描述的正交状态空间模型（O-SSM）是一种特殊类型的状态空间模型（SSM），其特点在于它使用了特定的基函数和测量函数来构建状态向量。

1. 状态空间模型（SSM）：SSM是一种用于描述动态系统的数学模型，通常由状态向量和输入信号组成。在这个定义中，SSM由一对函数$A(t)$和$B(t)$表示，这些函数定义了系统的动态行为。
2. 基函数$p_n(t,s)$和测量函数$\omega (t,s)$：在O-SSM中，基函数$p_n(t,s)$和测量函数$\omega (t,s)$是核心概念。基函数通常用于表示系统状态的不同方面，而测量函数用于加权这些状态。这些函数共同定义了系统如何响应输入信号。
3. 函数$K_n(t,s)$的定义：$K_n(t,s)$是通过乘积$p_n(t,s)\omega (t,s)$得到的函数，代表了系统在时间点$t$对过去输入的响应。这个函数是状态向量$x_n(t)$的积分核心，决定了系统如何从输入信号$u(s)$中提取信息。
4. 状态向量的积分表示：定义中的第一个积分式$x_n(t)={\int }_{-\infty }^t{K}_n(t,s)u(s)ds$表示状态向量$x_n(t)$是$K_n(t,s)$与输入信号$u(s)$的卷积。这意味着$x_n(t)$是输入信号历史的加权和，反映了系统对过去输入的“记忆”。
5. 正交性条件：定义中的第二个积分式${\int }_{-\infty }^t{p}_n(t,s)p_m(t,s)\omega (t,s)ds={\delta }_{nm}$表明，不同的基函数$p_n$和$p_m$在$\omega$加权下是正交的。这里的Kronecker delta函数${\delta }_{nm}$确保当$n$和m不相等时，这两个基函数的加权内积为零，而当$n$和$m$相等时为一。这种正交性是O-SSM的关键特征，它保证了状态向量的各个分量能够独立地表示输入信号的不同方面。

总之，定义5.1中的O-SSM是一种特殊的SSM，它通过使用正交基函数和特定的测量函数来精确地表示和处理输入信号的历史信息，从而使得状态向量可以高效且独立地捕获输入信号的不同特征。

命题5.2：如果一组核函数满足$ K_n(t, s) = p_n(t, s)\omega(t, s) $，其中函数$p_n $关于$\omega$是完备且正交的（即对于每个固定的$t$，$\langle p_n, p_m \rangle_{\omega} = \delta_{nm}$，或者说$p_n$是关于测度$\omega$的一个正交归一化基），那么$p$和$\omega$是唯一的。在此框架下，对于所有的$t$，状态向量$ x(t) $简单地表示为输入$ u$在$t$之前的投影到一个正交归一化基上，因此可以从$x(t)$重构u的历史。

命题5.3：考虑一个满足(5.4)的正交状态空间模型（O-SSM），并固定一个时间点$t$。进一步假设当$N$趋于无穷大时，$p_{nt}$在$\omega (t)$的支持上形成一个完整的基。那么对于所有$s \leq t $，都有$u(s) = \sum_{n=0}^{\infty} x_n(t) p_n(t, s)$。

命题5.4：不存在具有对角状态矩阵 A = diag { − 1 , − 2 , … } A = \text{diag}\{-1, -2, \ldots\} A=diag{−1,−2,…}的时间不变正交状态空间模型（TO-SSM）。

这些命题为理解正交状态空间模型（O-SSM）和时间不变正交状态空间模型（TO-SSM）提供了重要的理论基础。命题5.2和5.3关注的是如何用状态空间模型来表示和重构函数，而命题5.4则指出了在构建TO-SSM时的一个特定限制。

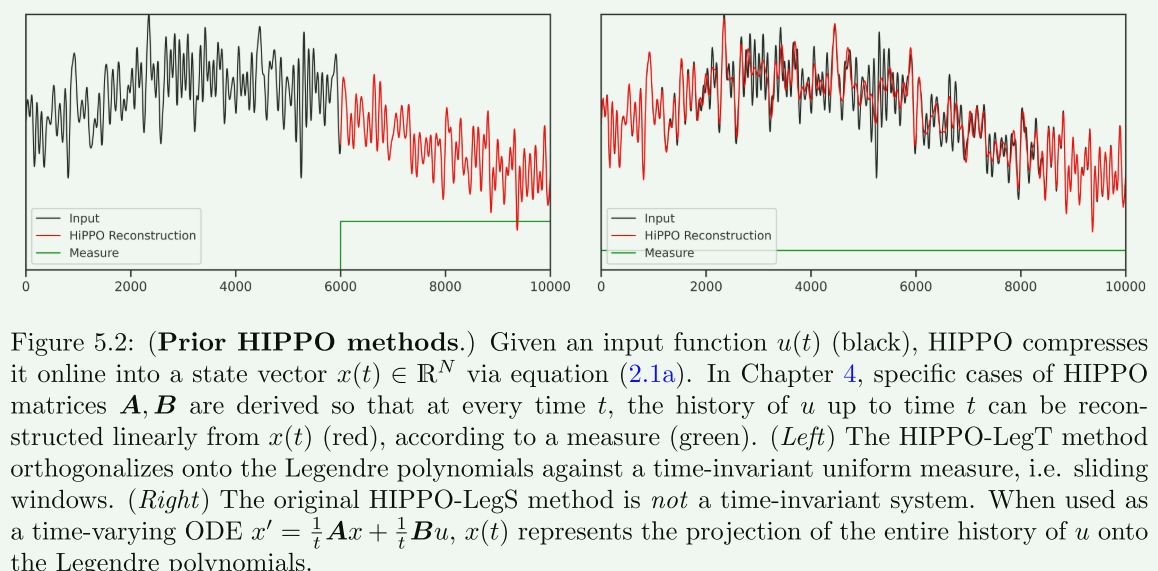
对上图的理解：该图展示了HIPPO方法的应用

• HIPPO压缩过程：给定一个输入函数$u(t)$(黑色曲线），HIPPO方法在线实时地将其压缩为一个状态向量$x(t)\in {\mathbb{R}}^N$，这一过程遵循方程(2.1a)。在第4章中，特定情况下的HIPPO矩阵$A$和B被推导出来，以便在每个时间点$t$，可以从$x(t)$（红色曲线）线性重构出直至时间$t$的$u$的历史，根据一个测量（绿色）。

• 两种方法：图中展示了两种不同的HIPPO方法。

  • 左图 - HIPPO-LegT方法：此方法将输入正交化到勒让德多项式上，对应于一个时间不变的均匀测量，即滑动窗口。

  • 右图 - 原始的HIPPO-LegS方法：这不是一个时间不变的系统。当使用作为一个时变常微分方程$x^{\prime }=\frac{1}{t}Ax+\frac{1}{t}Bu$，$x(t)$表示整个$u$历史的投影到勒让德多项式上。

这个图片说明了HIPPO方法如何将连续的输入信号压缩为状态向量，以及不同的HIPPO变体如何在不同的测量和假设下工作。

5.1.3 Previous HIPPO Methods

对于之前的HIPPO方法进行了讨论，主要集中在HIPPO-LegT和HIPPO-LegS两种方法上。

1. HIPPO-LegT:
   • 定义：该系统是一个时间不变的正交状态空间模型（TO-SSM），用于近似截断的勒让德多项式。这里用到的是勒让德多项式$L_n(t)$，经重新缩放使之在区间[0, 1]上正交归一化，即满足$\int L_n(t)L_m(t)I(t)dt={\delta }_{nm}$，其中$ I(t)$是单位区间[0, 1]上的指示函数。
   • 命题5.6：当$N$趋向于无穷大时，SSM使用(5.2)中的$(A,B)$矩阵，形成一个TO-SSM，其中$\omega (t)=I(t)$和$K_n(t)=L_n(t)I(t)$。
   • 应用：这个系统是HIPPO方法的前身，也被称为勒让德延迟网络（LDN）或勒让德记忆单元（LMU）。原始动机是找到一个最优的SSM近似来模拟具有脉冲响应$K(t)=\delta (t-1)$的延迟网络，表示一个延迟了1个时间单位的输出。
2. HIPPO-LegS:
   • 不同于HIPPO-LegT（一个线性时不变系统（LTI）或TO-SSM），HIPPO-LegS是在第4章中提出的，用于时变系统，其动态方程为$x^{\prime }(t)=\frac{1}{t}Ax(t)+\frac{1}{t}Bu(t)$。
   • 与HIPPO-LegT不同，后者是在滑动窗口$[t-1,t]$上重建截断的勒让德多项式，而HIPPO-LegS则是在“缩放”窗口$[0,t]$上重建勒让德多项式。由于窗口随时间变化，系统不是时间不变的。

总的来说，这两种方法展示了HIPPO框架在不同假设下的应用，其中HIPPO-LegT方法通过使用时间不变的正交状态空间模型来近似勒让德多项式，而HIPPO-LegS方法则利用时变系统来重建勒让德多项式，突显了HIPPO方法的灵活性和适应性。

补充说明：勒让德多项式（Legendre polynomials）是一系列在数学中广泛使用的正交多项式。它们的定义和性质包括：

1. 定义: 勒让德多项式是在区间[-1, 1]上的解析函数，通常以$P_n(x)$ 表示，其中 $n$ 是非负整数，代表多项式的阶。
2. 正交性: 勒让德多项式满足正交性质，即在区间[-1, 1]上对于不同阶的多项式，它们的积分为0。具体来说，如果 $m\ne n$，则有 ${\int }_{-1}^1{P}_n(x)P_m(x)dx=0$
3. 递归关系: 勒让德多项式可以通过递归关系式构造，其中第n阶多项式可以通过前两个多项式计算得出。
4. 应用: 勒让德多项式在物理学（特别是在量子力学和电磁学中解球坐标系下的问题）、工程学和数值分析等领域有广泛应用。
5. 生成函数: 勒让德多项式有相关的生成函数，这使得它们在解析问题时特别有用。

5.2 Generalizations of LegS

对HIPPO-LegS方法的推广进行了探讨

1. 推广的背景: 通过定理E.3，展示了一类特殊的时变正交状态空间模型（O-SSM），这些模型涵盖了HIPPO-LegS的时不变和时变版本。
2. 推论5.8: 定义了一个函数 $\sigma (t,s)=\exp (a(s)-a(t))$，其中 $a$ 是任意可微分的函数。这样的状态空间模型（SSM）($\left(a^{\prime }(t)A,a^{\prime }(t)B\right)$) 是一个O-SSM，具有以下特性：
   • 测量函数：$\omega (t,s)=I(\sigma (t,s))a^{\prime }(s)\sigma (t,s)$
   • 基函数：$p_n(t,s)=L_n(\sigma (t,s))$
3. 推论5.9 (Scale-Invariant HIPPO-LegS): 当设置 $a^{\prime }(t)=\frac{1}{t}$ 时，得到的SSM $\left(\frac{1}{t}A,\frac{1}{t}B\right)$ 是一个TO-SSM，其基函数 $K_n(t)=\frac{s}{t}{L}_n\left(\frac{s}{t}\right)$ 和测量函数 $\omega =\frac{1}{t}I[0,1]$，这里的$A$和$B$定义如公式(5.1)。
4. 推论5.10 (Time-Invariant HIPPO-LegS): 当设置 $a^{\prime }(t)=1$ 时，SSM $(A,B)$ 是一个TO-SSM，具有以下特性：
   • 测量函数：$\omega (t)=e^{-t}$
   • 基函数：$p_n(t)=L_n\left(e^{-t}\right)$

这些结果表明，可以通过调整基函数和测量函数的方式，将传统的HIPPO-LegS方法推广到不同的时间变化和时间不变的情况。这些推广方法在时间轴上对勒让德多项式进行了指数级“扭曲”或基础变换，从而实现了在不同时间尺度上对信号的正交表示。

5.3 Finite Window TO-SSMs

这一节主要讨论了在时间不变状态空间模型（TO-SSM）设置下，当SSM基函数 $K_n(t)$ 在有限窗口上支持时的情况。这些模型可以表示为滑动窗口变换。

1. HIPPO-FouT:
   • 使用了更通用的框架（定理E.3），不一定需要多项式作为基函数，而是得出一个将信号投影到截断的傅立叶函数上的TO-SSM。
   • 定理5.11: 当 $N\to \infty$ 时，对于式(5.3)的SSM是一个TO-SSM，其测量函数 $\omega (t)=\mathbb{I}(t)$，基函数集合 { p n } n ≥ 1 \left\{p_{n}\right\}_{n \geq 1} {pn​}n≥1​ 是在区间$[0,1]$ 上的截断傅立叶基函数，且正交。这些基函数以 { p n } n ≥ 0 = ( 1 , c 0 ( t ) , s 0 ( t ) , … ) \left\{p_{n}\right\}_{n \geq 0}=\left(1, c_{0}(t), s_{0}(t), \ldots\right) {pn​}n≥0​=(1,c0​(t),s0​(t),…) 的形式排列，其中 $s_{m}(t)=\sqrt{2} \sin (2 \pi m t) $ 和 $c_m(t)=\sqrt{2}\cos (2\pi mt)$，对于 $m=0,\dots ,N/2$。
2. 应用与优势:
   • 这个SSM对应于傅立叶级数分解，是信号处理中普遍使用的工具，但在这里以状态空间模型的形式表示。
   • 使用这些行为良好的基函数的优势在于可以利用傅立叶分析中的经典结果。例如，通过对截断的傅立叶基函数进行线性组合，可以表示区间 $[0,1]$ 上的任何函数，因此FouT可以表示任何局部卷积，即现代卷积神经网络的层。

5.4 Properties of TO-SSMs: Timescales and Normalization

讨论了时间不变状态空间模型（TO-SSMs）的属性，特别是时间尺度和归一化。

1. 初始化参数: 提出了关于如何为一个SS(S)M层正确初始化参数 $A,B,C$ 的问题。
2. 时间尺度 $\Delta$: 讨论了 $\Delta$ 在SSM模型中的直观意义以及如何设置。
3. 闭包属性: 展示了基本变换如何保持TO-SSMs的结构。对于TO-SSM $(A,B)$：
   • 标量缩放（Scalar Scaling）: $(cA,cB)$
   • 恒等位移（Identity Shift）: $(A+cI,B)$
   • 酉变换（Unitary Transformation）: $\left(VA{V}^{\ast },VB\right)$
4. 归一化:
   • 引理5.15（TO-SSM的归一化）: 对于任意输入 $u(t)$，$\Vert x(t){\Vert }_2^2=\Vert u{\Vert }_{\omega }^2={\int }_{-\infty }^{t}u(s{)}^2\omega (t-s)dt$。
   • 推论5.16: 对于具有概率测度的TO-SSM（即 $\omega (t)=1$）和任意恒定输入 $u(t)=c$，状态的范数 $\Vert x(t){\Vert }_2=c^2$，如果 $C$ 的条目是均值0方差1，则输出 $y(t)$ 的均值为0方差为 $c^2$。
5. 时间尺度:
   • 对于连续到离散时间的转换，涉及一个表示离散化步长的参数 $\Delta$。在TO-SSMs的上下文中，这相当于对基础SSM进行标量缩放。
   • 对于有限窗口TO-SSM（如LegT或FouT），离散化该系统的步长 $\Delta$ 相当于考虑具有步长1的系统 $(\Delta A,\Delta B)$，产生在区间 $\left[0,\frac{1}{\Delta }\right]$ 上精确支持的基函数。
   • 推论5.17和5.18提供了针对特定TO-SSM的离散时间推论。
6. 定义: 合适归一化的TO-SSMs $(A,B)$ 将建模预期长度为1的依赖关系，而 $\Delta$ 调节它以建模长度为$\frac{1}{\Delta }$的依赖关系，从而实现对TO-SSM上下文大小的细粒度控制。

基于以上定义得出两个推论和一个定义：

1. 推论5.17: 根据定理5.13，当 $N\to \infty$ 时，离散卷积核 $\overline{\mathbf{K}}\to {\mathbf{e}}_{\lceil {\Delta }^{-1}\rceil }$，即具有延迟 $\frac{1}{\Delta }$ 的离散延迟网络。
2. 推论5.18: 对于HIPPO-FouT矩阵 $A$ 和 $B$，根据定理5.11，当 $N\to \infty$ 时，离散卷积核 $\bar{K}$（取决于 $C$ 的选择）可以表示任何长度为 $\lfloor {\Delta }^{-1}\rfloor$ 的局部卷积。
3. 定义5.19 (TO-SSM的时间尺度): 定义 $\mathbb{E}[\omega ]=\frac{{\int }_0^{\infty }t\omega (t)dt}{{\int }_0^{\infty }\omega (t)dt}$ 为具有测量 $\omega (t)$ 的TO-SSM的时间尺度。如果TO-SSM具有时间尺度1，则称其为时间尺度归一化。

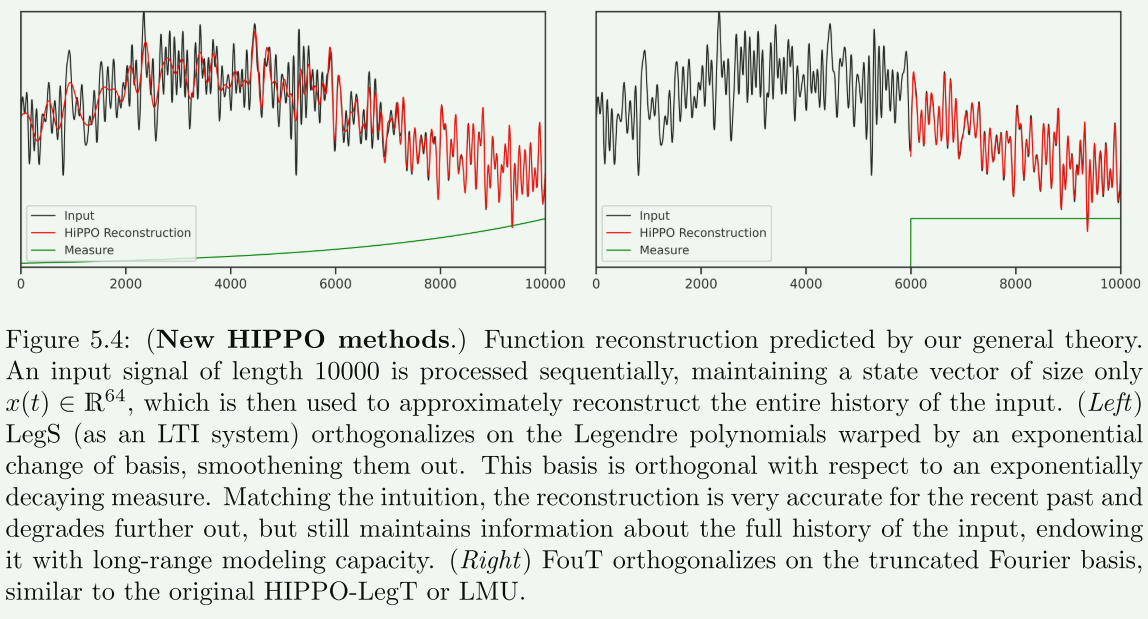
图5.4展示了基于一般理论预测的函数重建方法（新的HIPPO方法）。在这里，一个长度为10000的输入信号被顺序处理，并保持一个仅有64维的状态向量 $x(t)\in {\mathbb{R}}^{64}$，随后使用这个状态向量大致重建输入的整个历史。图中展示了两种方法：

1. LegS：作为线性时不变系统，它在勒让德多项式上进行正交化，并通过指数基变换使其变得平滑。这种基函数对应于指数衰减的测量。直观上，重建对于近期历史来说非常准确，但对于更远的历史则逐渐退化，尽管如此，它仍然保持了对输入完整历史的信息，赋予了它长期建模能力。
2. FouT：它在截断的傅立叶基础上进行正交化，类似于原始的HIPPO-LegT或LMU。

这些方法在理论上预测了函数重建的能力，展示了HIPPO框架在不同基函数和测量下的灵活应用。