熵相关概念（二）——交叉熵、JS散度、Wasserstein距离

原创已于 2025-01-20 15:09:21 修改 · 718 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #熵 #JS散度 #Wasserstein距离 #堆土机距离

于 2025-01-20 14:06:32 首次发布

基础知识专栏收录该内容

2 篇文章

订阅专栏

本系列已完结，全部文章地址为：

熵相关概念（一）——熵、KL散度-CSDN博客

熵相关概念（二）——交叉熵、JS散度、Wasserstein距离-CSDN博客

1 交叉熵

上一篇其实已经给出了交叉熵(Cross Entropy)的定义

$H(P,Q)=-\sum_xP(x)logQ(x)$

在深度学习的训练中，KL散度可以表示真实分布与拟合分布之间的距离，而KL散度=交叉熵-熵，真实分布的熵是固定的，不管拟合出什么分布，真实分布的熵是不变的，因此经常会看到使用交叉熵作为损失函数。

使用交叉熵代替均方误差还可以缓解梯度消失问题，见此文的说明熵、交叉熵、KL散度、JS散度 - Mrfanl - 博客园

特别地，对于二分类问题，P+Q=1，因此交叉熵可表示为

$L=-(ylog{\hat y}+(1-y)log(1-\hat y))$

其中y表示实际的标签， $\hat y$ 表示预测的标签。

2 JS散度

KL散度是非对称的，JS散度解决了此问题。

$JS(p||q)=\frac{1}{2}KL(p||\frac{p+q}{2})+\frac{1}{2}KL(q||\frac{p+q}{2})$ 。在GAN博文中就用到了JS散度。GAN对抗生成网络（一）——基本原理及数学推导_生成对抗网络推导-CSDN博客

3 Wasserstein距离

3.1 概念

Wasserstein距离也叫堆土机距离(Earth Mover's Distance)，假设概率分布A是土堆的分布状况，概率分布B是目标土堆的分布状况，用堆土机将A中的土堆削填变成B，堆土机路线最短距离称为堆土机距离。

以上是对“堆土”字面意义的理解，笔者再举一个例子，比如一个车企需要在全国各地设置制造厂，每个制造厂都要分配车床机器。分配机器的数量取决于当地政策、劳动力成本、上游零件运输成本、下游经销商运输成本、仓库空间等。当前车企在A省有3台机器，B省有4台机器，C省有1台机器，经过测算，最佳的分配是A省有1台，B省有5台，C省有2台。因此车企需要重新布局机器，在各省之间运输机器，达到最佳分配状态。考虑到A、B、C三省之间的距离，最短的运输距离就是堆土机距离。

3.2 数学表示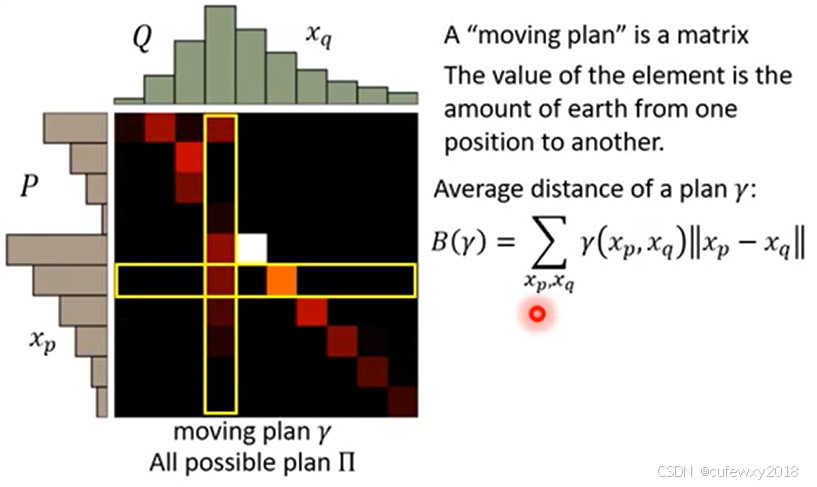

借用李宏毅老师的课件，符号表示如下：

符号	含义
P	分布之一
Q	分布之一
$x_p$	P分布中的取值
$x_q$	Q分布中的取值
$\gamma$	从P到Q每一个位置挪动的大小
B	moving plan对应的距离