线性代数矩阵转置乘法
Prerequisites:
先决条件:
The transpose of a matrix is a matrix whose rows are the columns of the original. In mathematical terms, A(i,j) becomes A(j,i) in the new matrix. Transpose has an important role in understanding and implementing Machine Learning algorithms. Major usage by Matrix Multiplication.
矩阵的转置是其行是原始列的矩阵。 用数学术语来说, A(i,j )在新矩阵中变为A(j,i) 。 转置在理解和实现机器学习算法中具有重要作用。 矩阵乘法的主要用法。
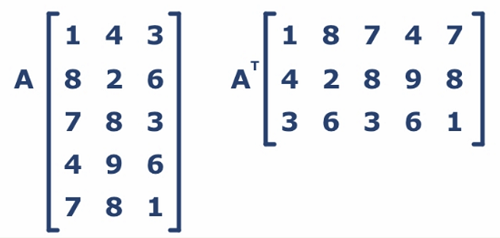
Method 1:
方法1:
Syntax:
transpose_M = M.T
Parameter:
Matrix M
Return:
MT
Method 2:
方法2:
Syntax:
transpose_M = numpy.transpose(M)
Input Parameter:
Matrix M
Return:
MT
转置矩阵的Python代码 (Python code for transpose matrix)
# Linear Algebra Learning Sequence
# Transpose using different Method
import numpy as np
g = np.array([[2,3,4], [45,45,45]])
print("---Matrix g----\n", g)
# Transposing the Matrix g
print('\n\nTranspose as g.T----\n', g.T)
print('\n\nTranspose as np.tanspose(g)----\n', np.transpose(g))
Output:
输出:
---Matrix g----
[[ 2 3 4]
[45 45 45]]
Transpose as g.T----
[[ 2 45]
[ 3 45]
[ 4 45]]
Transpose as np.tanspose(g)----
[[ 2 45]
[ 3 45]
[ 4 45]]
翻译自: https://www.includehelp.com/python/transpose-matrix.aspx
线性代数矩阵转置乘法







 本文介绍了线性代数中的矩阵转置概念,强调了转置在机器学习算法中的重要性,并提供了两种在Python中实现矩阵转置的方法,通过numpy库进行矩阵运算,最后展示了运算结果。
本文介绍了线性代数中的矩阵转置概念,强调了转置在机器学习算法中的重要性,并提供了两种在Python中实现矩阵转置的方法,通过numpy库进行矩阵运算,最后展示了运算结果。
















 737
737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








