目标检测（Object Detection）原理与实现(二)

基于霍夫变换和广义霍夫变换的目标检测

        上节讨论了基于阈值处理的目标检测，今天就来讨论下基于霍夫投票的目标检测，霍夫投票打算分成两个小节，第一个小节简单的说下霍夫变换和广义霍夫变换（generalized hough transform），他们投票的权重都是相等的，下一节讨论概率空间中的霍夫投票，顾名思义他们的投票权重是不确定的。

      先来看下霍夫变换（hough transform）,霍夫变换一般适用于有解析表达式的几何形状目标检测，例如直线、圆、椭圆等。用个统一的解析表达式来表达他们：f(x,alpha)=0,其中x 是图形上点，alpha则是解析表达式参数，比如欧式坐标系中直线的参数就是斜率m和截距c(或者极坐标系中的theta和ρ)，圆的参数则是原点和半径。霍夫变换的核心就是把图像空间的直线变换到参数空间（也叫霍夫空间），比如一个直线y=mx+c,给定一个点（x’,y’），把它代入直线方程，得到y’=mx’+c,其实此时仍然是一条直线（在参数空间的直线，斜率是-x’,截距是y’），图像空间和霍夫空间的对应关系如（图一）所示：

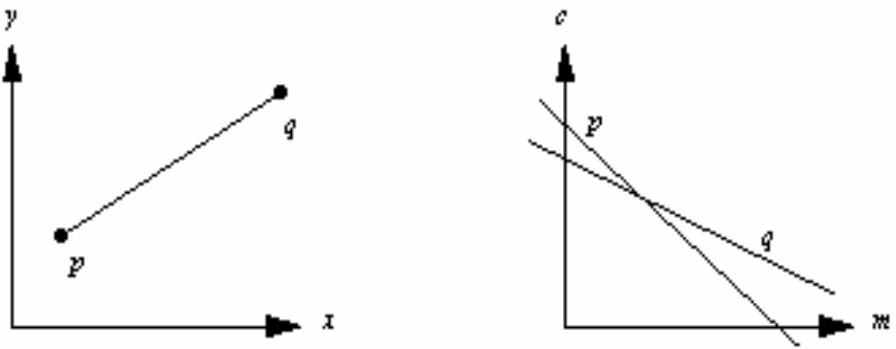
（图一）

     （图一）中左图是图像空间，右图是霍夫空间（参数空间），对于图像空间中线段pq上任意一点带入直线方程后，都可以在霍夫空间中得到另外一条直线，二者是对偶的，比如如（图一）所示，把两个端点带入后，在右图中得到的两个对偶直线，