神经网络学习笔记（五） 径向基函数神经网络

径向基函数神经网络

首先介绍一下网络结构：

1.输入层为向量，维度为m，样本个数为n，线性函数为传输函数。

2.隐藏层与输入层全连接，层内无连接，隐藏层神经元个数与样本个数相等，也就是n，传输函数为径向基函数。

3.输出层为线性输出。

理论基础

径向基函数神经网络只要隐含层有足够多的隐含层节点，可以逼近任何非线性函数。
在拟合函数的时候，我们要尽量的经过每一个点，但是当一大堆散乱数据的时候我们如果经过每一个点就造成过拟合，也就是根本无法寻找里面的隐含规律，我们需要一个权值均衡的拟合方式，这时候就要用到最小二乘法。

那么我们对样本点附近的点用什么方法插值呢？
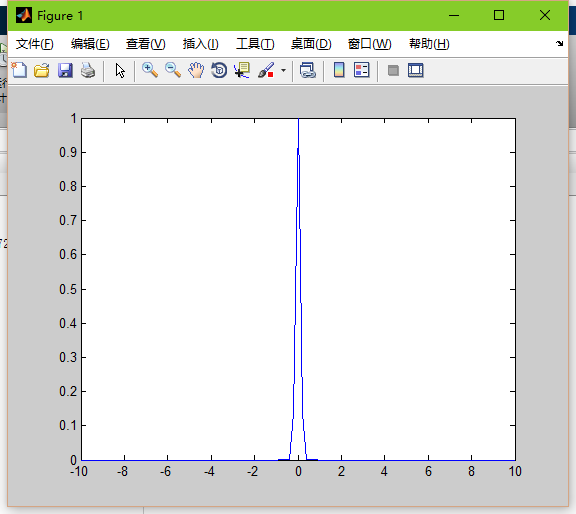
这就是基函数的作用了。通常我们将基函数设为高斯函数，那么高斯函数里面就涉及到两个参数了：sigma和距离d

高斯函数： exp（-d^2/(2*sigma^2)）;

sigam就是平滑因子，他可以控制高斯函数的平滑度。

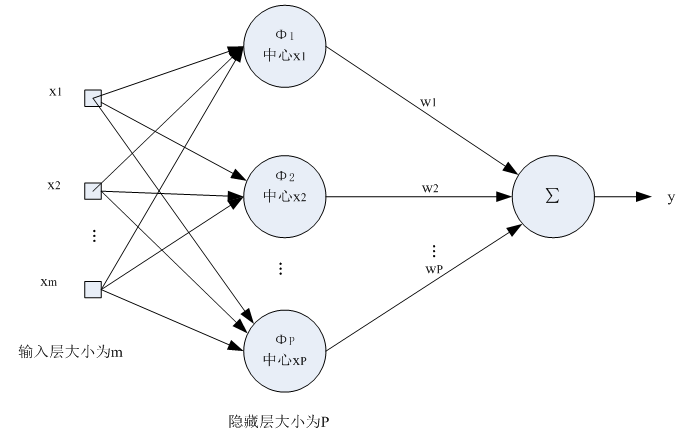
sigma=10

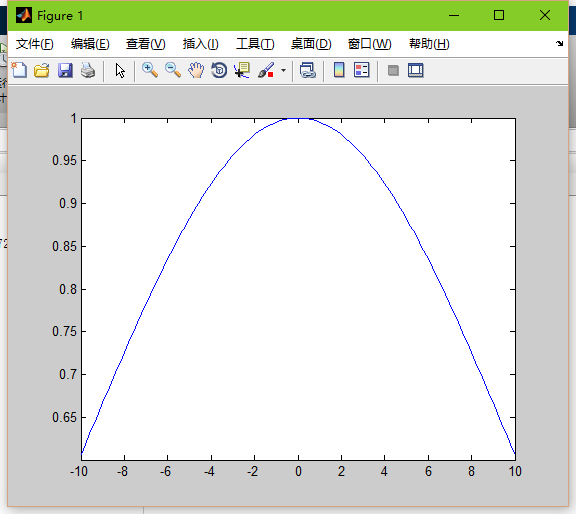
sigma=5

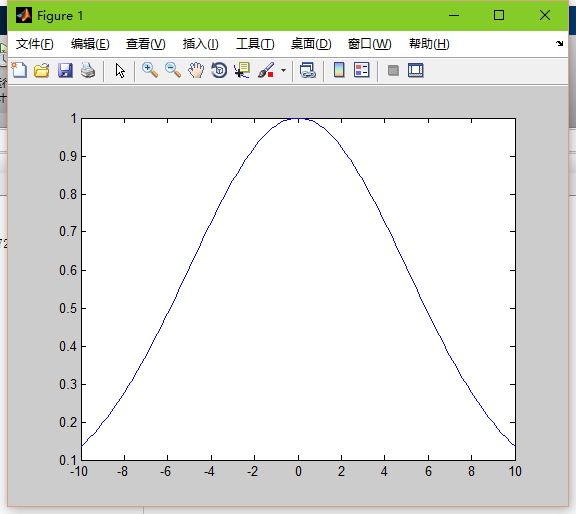
sigma=1

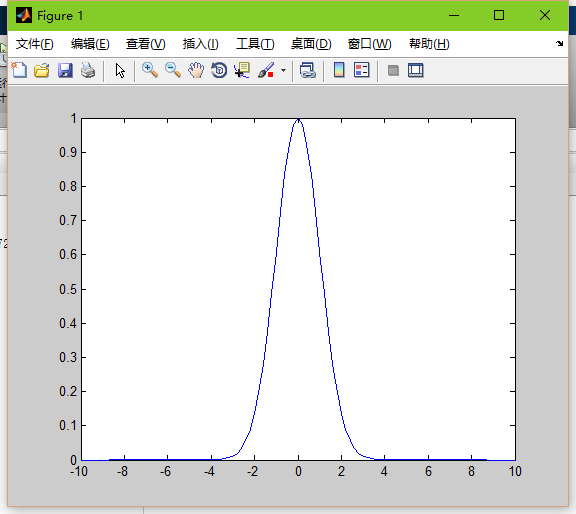
sigma=0.1

当平滑因子较低时，高斯函数就会尖锐，也就是边缘点的权值会很小，导致过拟合。

那么距离d是什么呢？

距离d就是向量离每一个隐含层中心的距离，通常隐含层的中心对应每个节点，所以每个距离就是节点矩阵自身相对自身每个点的距离。

距离表示着离节点越近，所受该节点的输出影响就越大。

下面就来实现一下这个神经网络

matlab（非API实现）

1.定义一些变量：

data=-9:1:8;
x=-9:.2:8;
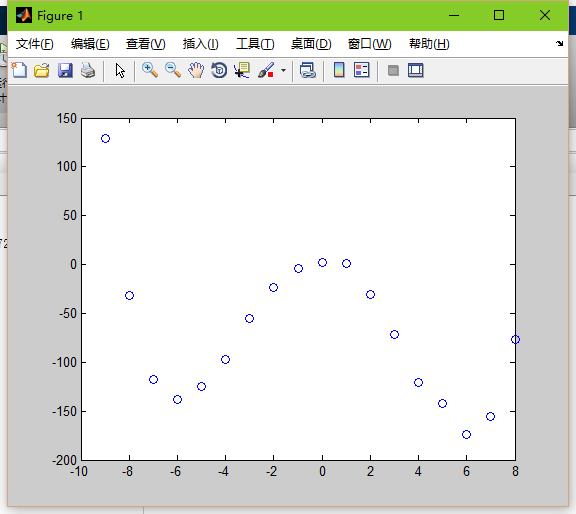
label=[129,-32,-118,-138,-125,-97,-55,-23,-4,2,1,-31,-72,-121,-142,-174,-155,-77];

spread=2;

spread就是sigma值 也称平滑度。
data为实际数据。
x为测试数据。
label表示目标输出。

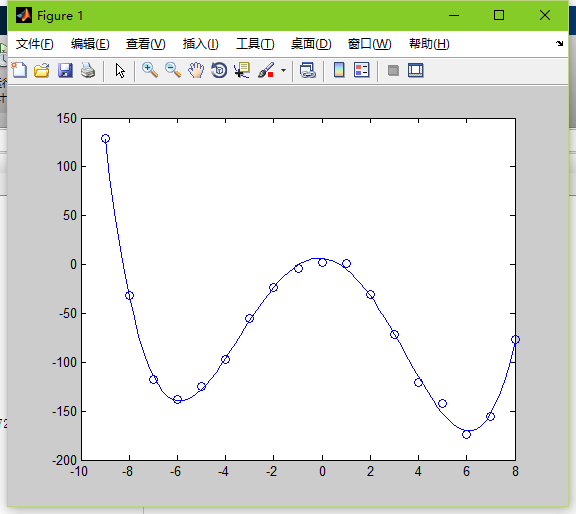
2.看一下输出点

plot(data,label,'o');
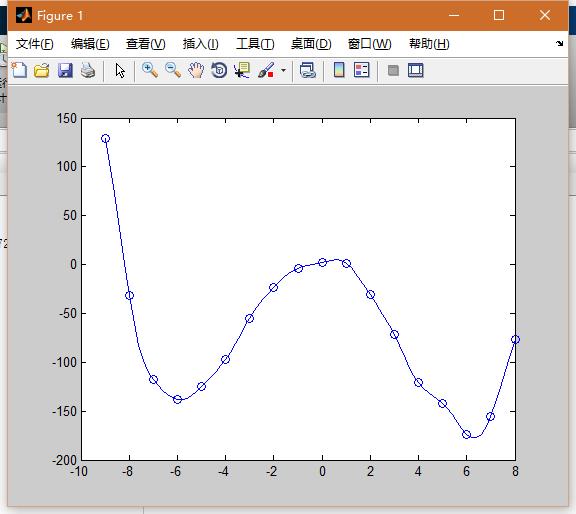
hold on;

3.拟合这条曲线的权值

dis=dist(data',data); %求距离

gdis=exp(-dis.^2/spread);%gauss

G=[gdis,ones(length(data(1,:)),1)];%广义rbf网络 （加入一个恒为1的隐含层节点）

w=G\label';%最小二乘的矩阵求解

4.测试所拟合的权值

chdis=dist(x',data);

chgdis=exp(-chdis.^2/spread);

chG=[chgdis,ones(length(x(1,:)),1)];

chy=chG*w;

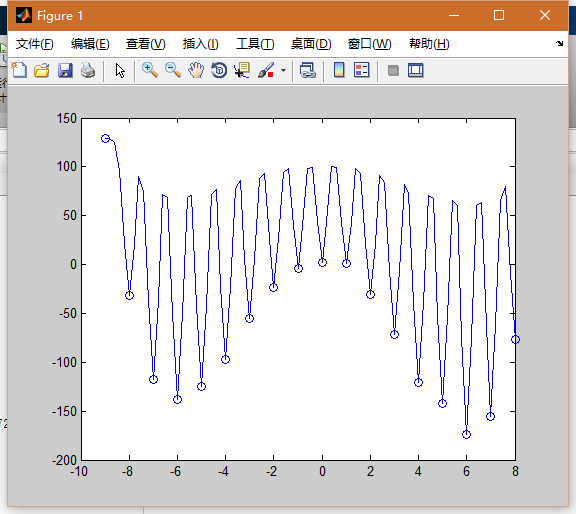
plot(x,chy);

如果将spread取0.1

节点附近的插值点的全脂会非常小导致曲线过拟合。

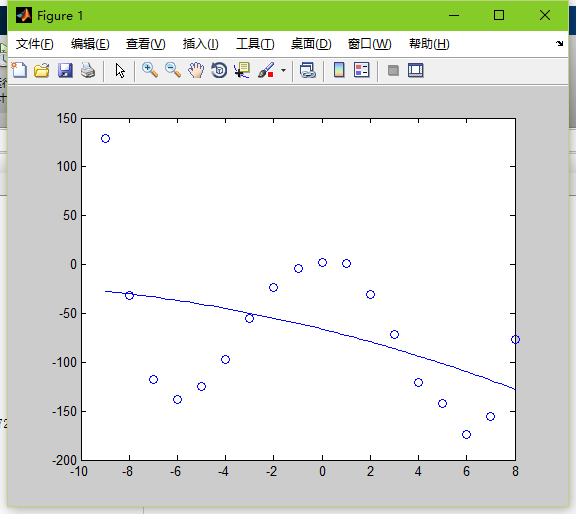
如果将spread取50000

很多点都已经偏离，曲线过于平滑。导致欠拟合。

如果再加2个0，取5000000

这个sigma太大了，直接会导致函数不拟合。

结束语

径向基函数有着bp算法不能达到的拟合效果，在拟合曲线上，径向基函数更快，更准确。
下一节我们会讨论优化的变种径向基函数神经网络—-广义回归神经网络（GRNN）。