CS229逻辑回归

逻辑回归的提出

在二分类问题中我们需要将离散的数据进行归类，首先我们规定正向类和负向类分别用1和0表示。按照一般我们使用线性分类处理，公式如下：

这时输出的y可能会远大于1或者远小于1，这时我们像能不能将输出值限制在0到1之间。

函数模型

将逻辑回归的输出变量的范围规定在0，1之间，其模型的假设是：

其中g函数使用sigmoid函数：

将z用线性组合代替：

函数图像为：

h函数的作用在于对于给定输入变量，根据选择的参数计算输出变量=1的可能性，即

在逻辑回归中，我们预测：

当大于等于0.5的时候，预测y=1；

当小于0.5的时候，预测y=0。

判定边界

结合sigmoid函数的图像可知，z=0的时候，g（z）=0.5,；z>0的时候，g（z）>0.5；z<0的时候，g（z）<0.5，然而$\mathbb{Z}={\theta }^{T}X$，所以当${\theta }^{T}X>0$时，预测y=1；当${\theta }^{T}X<0$，预测y=0。所以我们可以以${\theta }^{T}X=0$为该模型的分界线，将预测为1的区域和预测为0的区域隔离开。

代价函数

线性回归模型的代价函数是误差平方和理论上说逻辑回归可以沿用这个，但是我们将$h_{\theta }(X)=1/1+{\exp }^{-}{\theta }^{t}x$带入到误差平方和的代价函数中，我们得到的代价函数是一个非凸函数如下图：

而非凸函数，意味着将会由多个极小值点，那就会影响优化函数寻找全局最小值。所以我们的代价函数应该是凸函数。
所以我们从新设计逻辑回归的代价函数：
$J(\theta )=1/m\sum Cost(h_{\theta }(X^{(i)},y^{(i)})$即：

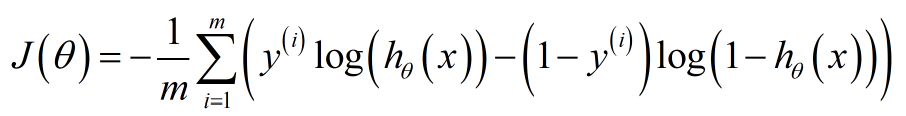
如何证明该函数是一个凸函数，需要验证该函数的二阶导数是正定矩阵。
我们假设f(x)为凸函数，且在x0处取得极小值，那么将该函数泰勒展开得：
$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+1/2f^{\prime \prime }(x_0)(x-x_0{)}^2$
$f^{\prime }(x_0)$=0，那么要使f(x0)为极小值就要让$f^{\prime \prime }(x_0)$大于等于0。
对于矩阵函数来说，将其泰勒展开为：

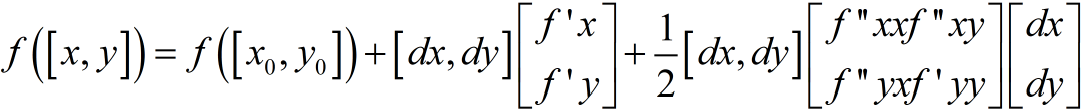
这是在一阶导数为0的情况下，是不是极小值取决于二阶导数矩阵是否非负，即$\Delta xH\Delta x>=0$，其中H矩阵就是二阶导数矩阵hession矩阵，我要验证hession矩阵是否正定。

优化函数

对于利用大量的数据去不断的优化参数，找到最合理的参数$\theta$使得代价函数最小，这是根据参数$\theta$确定的直线$\theta X=0$即为二分类的分界线。
优化函数一般采用梯度下降法，即${\theta }_j={\theta }_j-▽J_{\theta }({\theta }^{T}X)$
也可采用牛顿法优化函数，即：${\theta }_j={\theta }_j-▽J_{\theta }({\theta }^{T}X)/{▽}^2{J}_{\theta }({\theta }^{T}X)$

牛顿法：

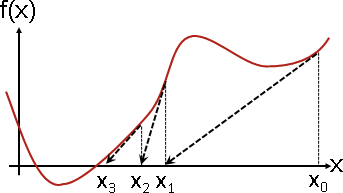
如上图所示，我们寻找f(x)=0处的点，则
1.初始化一个x0点，计算该点处的的导数f’(x0),并求出该点的切线方程。
2.切线与x轴的交点作为x1,然后计算x1处的切线方程。
3.重复1，2两步直到逐渐接近f(x)=0。
它的更新规则是：
$\theta =\theta -f({\theta }^0)/f^{\prime }({\theta }^0)$
将牛顿法应该用到逻辑回归中，就是求f’(x)=0,则将上面的f(x)替换为f’(x)可得：
$\theta =\theta -f^{\prime }({\theta }^0)/f^{\prime \prime }({\theta }^0)$

牛顿法为什么比梯度下降法收敛的快？
从本质上将牛顿法是二阶收敛，而梯度下降大是一阶收敛。通俗的讲，梯度下降法在优化时他会看到如何走下一步，而牛顿法不光会看到下一步如何走，也会看到走了下一步后在下一步是否好走。
这里也有人说：从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。