线性代数教程 线性方程组

CSDN 的文档显示有一些问题，一些数学符号显示不正确，想看 word文档 的可以移步到 github ： LearningDocuments/学习资料/平台无关/线性代数 at master · IceEmblem/LearningDocuments · GitHub

线性方程组消元解法

消元解法

1） 2x + 3y = 8

2 ）x + 2y = 5

解

(2x + 3y) - 2(x + 2y) = -y = 8 - 10 = -2

将y带入1得x = 1，y = 2

我们将这种解法消元解法

增广矩阵

如下线性方程组

a11x1 + a12x2 + ... + a1nxn = b1

a21x1 + a22x2 + ... + a2nxn = b2

...    ...   ...   ....

am1x1 + am2x2 + ... + amnxn = bm

我们可构建矩阵如下矩阵，Ax = b

我们把由A和b组成的矩阵称为增广矩阵，如下

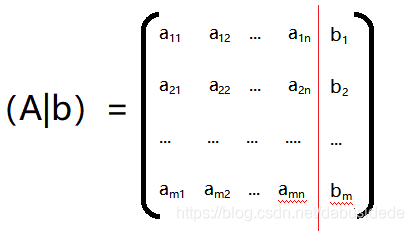
如下，我们用增广矩阵解线性方程组

2x1 + 2x2 - x3 = 6

x1 +  2x2 + 4x3 = 3

5x1 + 7x2 + x3 = 28

增广矩阵为

我们利用初等变换对矩阵的行进行变换，如下

解得：x1 = 1，x2 = 3，x3 = 2

实际上消元解法的过程就是初等变换的过程

阶梯形矩阵

我们称如下形式的矩阵称为阶梯形矩阵

其具有阶梯形状

阶梯形矩阵中，每行开头的元素是1，且它所在的列其他元素为0，则称简化的阶梯形矩阵，如下便是一个简化的阶梯形矩阵

增广矩阵与线性方程组

增广矩阵实际上就是线性方程组，如下增广矩阵

其线性方程组为

1. 1*x1 + 0*x2 + 0*x3 = 1
2. 0*x1 + 1*x2 + 0*x3 = 3
3. 0*x1 + 0*x2 + 1*x3 = 2

我们的增广矩阵通过初等变换转为其他矩阵实际上就是线性方程组1，2，3之间的相加减或者某个方程式的左右2边同乘k倍

无解的增广矩阵

如下矩阵

第3行，不存在 0*x1 + 0*x2 + 0*x3 = 2 ，所以该方程组无解

无穷多解的增广矩阵

如下矩阵，其第4行第4个元素为0，所以无法消去1到3行第4个的元素，其左边的矩阵等价于右边的矩阵

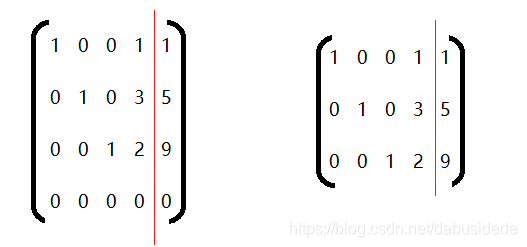
其对应的方程组为

1. 1*x1 + 0*x2 + 0*x3 + 1x4 = 1
2. 0*x1 + 1*x2 + 0*x3 + 3x4 = 5
3. 0*x1 + 0*x2 + 1*x3 + 2x4 = 9

所以方程组的解为

x1 = 1 - x4

x2 = 5 - 3x4

x3 = 9 - 2x4

x4 = c

当x4等于某个数值c是，我们带入x4去求x123