斐波那契数列的三种解法及时间复杂度

斐波那契数列：
f(n)=f(n-1)+f(n-2)(n>2) f(0)=1;f(1)=1;
即有名的兔子繁衍问题
在本篇文章我将会给出三种解法
递归

(1)递归：函数自己调用自己
(2)递归的"缺陷"：递归到一定程度，会发生"栈溢出"
(3)递归的"时间复杂度"：递归总次数*每次递归的次数
(4)递归的"空间复杂度"：递归的深度*每次递归空间的大小（注意："每次递归空间的大小"是个常数，可以基本忽略不计）
    递归的"深度"：树的高度（递归的过程是一个"二叉树"）

1.递归实现斐波那契数列

#include<stdio.h>
#include<stdlib.h>
long long Fib(long long N)
{
    if (N < 3)
        return 1;
    else
        return Fib(N - 1) + Fib(N - 2);
}
int main()
{
    long long num = 0;
    num=Fib(10);
    printf("递归：%d\n", num);
    system("pause");
    return 0;
}

运行结果：

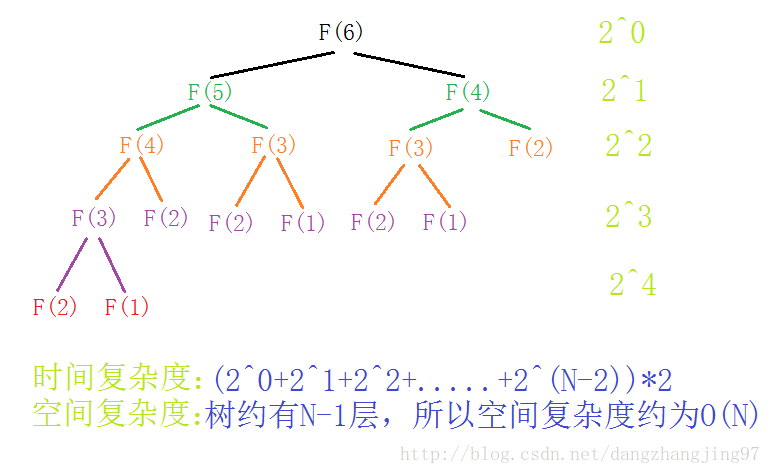
此种方法的缺陷：重复计算的次数太多，效率低
   例如：在下图中，F(3)就重复计算了 "3次"
时间复杂度：O(2^N)
空间复杂度：O(N)

2.递归（尾递归）实现斐波那契数列，但是时间复杂度尽可能低

尾递归是什么呢？
尾递归解决了递归重复计算的问题

"尾递归的前提是递归"
(1)定义：在一个程序中，执行的最后一条语句是对自己的调用，而且没有别的运算

(2)尾递归的实现：是在编译器优化的条件下实现的

  编译器优化：
     递归的第一次调用时会开辟一份空间，此后的递归调用不会再开辟空间，而是在刚才开辟的空间上做一些修改，实现此次递归，例如在本题中求Fib（10），编译器会给Fib（10）的调用开辟栈帧，调用Fib（9）的时候不会再重新开辟栈帧，而是在刚开辟的栈帧上做一些修改，因为递归的每一次调用都是一样的流程，只是会有一些数据不同，所以不会再开辟空间。

注：vs一般都支持优化，Debug下编译器不会优化哦，一定要在Release模式下。

#include<stdio.h>
#include<stdlib.h>
long long Fib(long long first,long long second ,long long N)
{
    if (N < 3)
        return 1;
    if (N == 3)
        return first + second;
    return Fib(second, first + second, N - 1);
}
int main()
{
    long long num = 0;
    num=Fib(1,1,10);
    printf("尾递归：%d\n", num);
    system("pause");
    return 0;
}

运行结果：

此种方法是尾递归，很大程度的减小了第一种方法（递归实现斐波那契数列）的时间复杂度
时间复杂度：O(N-2)约等于0(N)
空间复杂度：O(N-2)约等于0(N)（编译器如果优化的话是O（1））

此种递归是尾递归

3.循环实现斐波那契数列

#include<stdio.h>
#include<stdlib.h>
long long Fib(long long N)
{
    long long first = 1;
    long long second = 1;
    long long ret = 0;
    for (int i = 3; i <=N; ++i)
    {
        ret = first + second;
        first = second;
        second = ret;
    }
    return second;
}
int main()
{
    long long num = 0;
    num=Fib(10);
    printf("循环：%d\n", num);
    system("pause");
    return 0;
}

运行结果：

时间复杂度：O(N)
空间复杂度：O(1)（创建了四个对象，是常数，所以可忽略不计）
此种方法是"最优方法"
优点：时间复杂度和空间复杂度最低，而且可读性高